WaDGAN-AD를 이용한 전력 소비 패턴의 비지도 학습 기반 이상 탐지
© 2021 KIIE
Abstract
Anomaly detection in time series is essential because it can detect outlying patterns such as a breakdown in machines and fraudulent customers. Among many anomaly detection domains, detecting abnormal patterns in energy consumption is used to detect technical breakdown in factories, general buildings, or energy theft in households. To overcome the limitations of previous studies, this paper suggests WaDGAN-AD, which combines generative adversarial network (GAN) and Long Short-Term Memory (LSTM) and applies two structural improvements. WaDGAN-AD has stacked discriminator LSTM layers to more precisely learn feature representations of time series data. Also, it has different numbers of hidden units in each hidden layer of LSTM to consider multiple cycles appearing in a single time-series data. Experimental results based on synthetic datasets and real datasets show that WaDGAN-AD can better detect abnormal energy consumption than benchmark methods.
Keywords:
Time-series Anomaly Detection, LSTM, GAN, Energy Consumption1. 서 론
기존 건물들의 전력 소비량 중 약 1%에서 2.5%가 장비의 오작동 및 이상 현상에 의해 발생하는 것으로 알려져 있다(Wiggins and Brodrick, 2012). 이러한 상황에서 건물의 전력 소비량에서 발생하는 이상치를 적절히 감지할 경우 건물 운영에 소요되는 전력 소비량을 최소 5%에서 최대 30%까지 줄일 수 있는 것으로 나타났다(Bynum et al., 2012; Dong et al., 2014). 공정의 기계에서 발생하는 전력 소비량도 유사한 현상을 보인다. DataRPM(2017)의 자료에 의하면 산업 현장에서의 갑작스러운 셧다운(shutdown)으로 발생한 에너지 손실로 인한 비용이 하루에 약 5,000만 원에 달할 만큼 낭비가 크다고 알려져 있다. 그러나 산업 현장에서 사용되는 에너지 소비패턴의 이상치 탐지가 적절히 수행된다면 전력 소비의 불확실성을 90%가량 감소시킬 수 있으며, 현장 노동자들의 작업 효율성을 25%가량 향상시킬 수 있는 것으로 보고되었다(DataRPM, 2017). 따라서 전력 사용량에서의 이상치 탐지는 일반 빌딩에서의 갑작스러운 셧다운 문제, 공정에서의 장비 고장, 가정집에서의 정전 문제 및 소비자의 의도적 탈취(energy theft)(Jiang et al., 2014)등의 이상 행위를 정확하게 탐지하여 전체 전력 사용량 및 비용을 감축하는 데 유용하게 사용될 수 있다(Chou and Telaga, 2014).
시계열 데이터에서의 이상치 탐지란 시간의 흐름에 따라 연속적으로 발생하는 데이터로부터, 과거에는 발생하지 않던 현상을 실시간으로 그리고 자동으로 탐지하는 것을 의미한다(Chandola et al., 2009). 전력 분야의 시계열 데이터는 주기성 및 경향성을 갖는 데이터이며 이 중 비정상적인 주기 및 갑작스러운 경향성의 변화를 탐지하는 것은 여러 분야에 사용될 수 있다. 먼저 스마트 팩토리 분야에서는 기계를 작동하는 과정에서 수집되는 시계열 데이터의 실시간 모니터링을 통해 이상 패턴을 감지함으로써 고장 및 오작동을 사전에 방지하여 생산비용의 손실을 감소시킬 수 있다(Hsieh et al., 2019). 또한, 전력 소비량의 이상치 탐지를 통해 에너지 탈취(McLaughlin et al., 2009)를 감지할 수 있으며 이를 통해 전력 사용자가 의도적으로 스마트 미터기를 조작하여 에너지의 사용량을 기존 패턴보다 확연히 감소시켜, 비용을 감소시키려는 위법 행위를 방지할 수 있다(Jiang et al., 2014). 또한, 일반 건물에서도 전력 소비량 시계열 데이터 값이 갑작스럽게 급감한다면 해당 건물에서 발생하는 정전 및 셧다운 문제로 판단할 수 있고 이를 토대로 적절한 비상조치를 실시간으로 취할 수 있게 된다(Ren et al., 2018).
시계열 전력 데이터에 대한 이상치 패턴을 수행하는 기존 연구들은 주로 머신러닝과 딥러닝 기법들을 활용하였다. 특히, 딥러닝 기법을 활용한 선행 연구에서는 주로 순환신경망(recurrent neural network, RNN) 기반의 Long Short-Term Memory(LSTM)과 오토인코더(autoencoder, AE)만을 사용하여 전력 소비량에서의 이상치 탐지를 시도하였으나, 이는 정상 데이터와 이상치의 미세한 차이까지는 구분하지 못한다는 한계가 존재한다(Pereira and Silveira, 2018). 데이터의 특성 관점에서 보면 현실에서 발생하는 전력 소비량 시계열 데이터는 연, 분기, 월, 주, 일 등 여러 길이의 주기가 통합된 시계열 데이터라는 특징을 갖는다. 이러한 복잡한 특성을 이상치 탐지 모델에 학습하기 위해서는 여러 개의 은닉층으로 RNN을 구성하고, 각 은닉층마다 다양한 은닉 노드 수를 갖도록 설계해야 하나, 기존 연구들은 비교적 단순한 구조의 모델로 이상치 탐지를 수행하고 있어 낮은 이상치를 검출력을 나타내는 한계점을 보여주었다(Bashar and Nayak, 2020; Li et al., 2018). 마지막으로 기존 선행 연구 중 지도 학습 기반의 시계열 이상치 탐지 연구의 경우, 전력 소비량 데이터에서 정상 또는 비정상을 의미하는 정답 레이블이 존재해야 모델을 학습시킬 수 있지만(Coma-Puig et al., 2016) 현실에서 발생하는 전력 소비량 데이터는 이러한 정답 레이블을 포함하지 않고 있다(Fan et al., 2018). 전력 소비량 데이터에 정상 또는 비정상의 정답 레이블을 부여하는 과정은 상당한 시간과 전문성을 갖춘 인력의 노동력을 필요로 하므로 지도 학습 기반의 이상치 탐지 방법론을 현실에 적용하는 것은 뚜렷한 한계가 있다(Fan et al., 2018).
본 논문은 기존 선행 연구들의 한계점들을 극복하기 위해 WaDGAN-AD를 제안한다. WaDGAN-AD는 기존 LSTM 기반 모델 구조에 적대적 생성 신경망(generative adversarial network, GAN)을 추가하여, 기존의 잔차(residual) 손실로 이상치를 탐지하는 방식에 구분자 손실(discriminator loss)을 함께 고려하는 방식을 도입하여 더욱 미세한 차이까지 감지할 수 있게 하였다. 또한, GAN의 구성 요소인 LSTM의 구조를 발전시켜 시계열 데이터에서의 이상치 탐지 성능을 높이고자 하였다. 마지막으로 비지도 학습 기반의 모델을 제안함으로써 정답 레이블이 없는 전력 소비량 데이터에서도 이상치를 탐지할 수 있게 하였다. 제안한 WaDGAN-AD의 효과를 검증하기 위해 본 연구에서는 가상의 인공 데이터와 실제 건물에서 생성된 전력 소비량 시계열 데이터를 사용하여 실험을 수행하였다. 제안한 모델의 학습은 실제 전력 데이터만을 사용하여 수행하였으며, 이상치 탐지 성능을 평가하기 위해 테스트 데이터의 일부는 전력 분야에서 이상치가 발생할 수 있는 현실적인 시나리오를 고안하여 각 시나리오에 맞는 이상치 데이터를 생성하여 구성하였다. 제안한 모델 구조의 검증은 내포된 주기의 개수가 서로 다른 인공 데이터들을 생성하여 진행하였다.
본 연구의 구성은 다음과 같다. 먼저 제2장에서 전력 데이터상의 이상치 탐지를 수행한 선행 연구와 시계열 데이터상의 이상치 탐지에 관한 선행 연구를 소개한다. 이후 제3장에서 WaDGAN-AD 모델을 설명한 뒤, 제4장에서 수행한 실험의 설계 및 결과를 서술한다. 마지막으로 제5장에서는 본 연구의 결과 및 추후 연구 방향에 대해 서술하였다.
2. 선행 연구
전력 소비량 데이터를 활용하여 전력 탈취, 전력 네트워크상의 고장 등 전력 사용량의 이상치를 탐지하는 연구들은 정답 데이터 활용 여부에 따라 크게 비지도 학습 방식과 지도 학습 방식으로 구분할 수 있다. 비지도 학습 방식은 전력 소비량의 이상치 데이터를 탐지하는 모델을 학습하는 과정에서 전력 소비량의 정상/비정상 여부에 대한 정답 레이블이 필요하지 않기 때문에, 레이블을 부여하는 시간과 자원이 필요하지 않는다는 장점이 있다. 비지도 학습 기반의 전력 소비량 이상치 탐지 연구들은 다시 머신러닝 기법과 딥러닝 기법을 사용한 연구들로 세분화할 수 있다.
우선 비지도 학습을 기반으로 한 머신러닝을 사용한 연구 중 Angelos et al.(2011)은 먼저 Fuzzy C-Means(FCM) 클러스터링을 통해 비슷한 전력 소비자들의 집단을 찾기 위한 군집화를 진행하였다. 그 후, 전력 탈취의 가능성이 있는 비정상 소비자를 탐지하기 위해 Fuzzy classification을 적용하였다. 해당 연구는 FCM을 통해 각 군집별로 속할 가능성을 확률 값으로 표현하여 유연하게 소비자의 군집을 표현할 수 있다는 장점이 있지만, 군집화 이전에 군집의 개수를 지정해야 한다는 점, 소비자의 전력 소비패턴을 몇 개의 속성 및 어떤 속성으로 표현할 것인지(해당 연구에서는 5개의 사전 정의된 속성을 사용)도 사전에 선정해야 한다는 단점이 존재한다. Qiu et al.(2018)의 연구에서는 소비자의 전력 소비 데이터를 주성분 분석을 통해 2차원으로 차원을 축소한 후, 그리드 프로세싱(Grid Processing)을 통해 높은 밀도의 그리드에 존재하는 데이터는 정상 데이터일 것이라 가정하고 해당 데이터를 이상치의 후보에서 제외하였다. 그 후 나머지 데이터에 대한 Local Outlier Factor(LOF)를 계산하여 최종 이상치 점수를 도출하였다. 이 연구는 전체 데이터 중 이상치는 극소수로 존재한다는 특징을 활용하여 그리드라는 개념을 도입하였고 이로 인해 보다 효율적인 이상치 탐지를 가능하게 한다는 장점이 있다. 그러나 모델의 첫 단계에서 밀도를 기반으로 정상과 비정상을 분류하고 시작하기 때문에 흩어진 분포의 데이터를 해당 모델에 적용할 시 오류가 크다는 단점이 존재한다.
비지도 학습 기반 전력 이상치 탐지 연구는 머신러닝에 그치지 않고 딥러닝을 활용한 모델들로도 확장되었다. 대표적인 예시로 Weng et al.(2018)은 학교 교정 내에서 발생하는 전력 소비량의 이상치 탐지를 위해 LSTM 기반의 오토인코더 모델을 구축하였다. 정보의 압축을 수행하는 인코더와 이를 다시 복원하는 디코더 구조를 통해 출력 데이터를 입력 데이터와 동일한 차원으로 재구축할 수 있으므로 입력 데이터와 모델에 의해 재구축된 출력 데이터의 차이를 계산하여 그 값이 크면 비정상적인 전력 사용량이라고 정의하였다. 해당 연구는 LSTM을 여러 층 쌓아, 상대적으로 여러 특징이 중복해서 발생하는 복잡한 시계열 데이터를 분석할 수 있다는 장점이 있는 반면에, 단순하게 재구축 오차만을 고려했다는 점에서 이상치의 미세한 차이까지는 감지하지 못한다는 단점이 존재한다(Audibert et al., 2020).
전력 분야가 아닌 일반적인 시계열 데이터에서 비정상적인 패턴을 검출하는 연구 중 다수가 GAN을 기본 모델로 사용하였다. 우선 Li et al.(2018)은 GAN의 생성자와 구분자를 LSTM으로 구성하여 시계열 데이터를 처리하는 GAN-AD 모델을 제안하였다. 해당 모델은 GAN의 생성자와 구분자가 상호 작용으로 학습한다는 점을 활용하여 시계열 데이터 패턴을 모델에 학습시켰다. 이때 검증하고자 하는 데이터가 모델에 입력되었을 때, 해당 시계열 데이터에 상응하는 잠재 벡터를 생성자에 입력해야 하는데, 이렇게 잠재 벡터를 찾는 기법으로 도치 매핑(invert mapping)이라는 알고리즘을 적용하였다. 해당 연구는 GAN을 최초로 시계열 이상치 탐지에 적용했다는 의의가 있으나, GAN의 특성상 학습 시 생성자의 손실 함숫값이 수렴하지 않는다는 단점이 발생할 수 있고, LSTM의 층 수나 은닉 노드 수에 대한 구조가 비교적 단순하여 경향성이나 주기성을 갖는 복잡한 시계열 데이터를 분석하고자 할 때, 해당 특징들을 모두 고려하지 못한다는 한계점이 존재한다. 그 후 Li et al.(2019)은 GAN-AD와 동일한 구조를 갖지만, 이상치 점수를 시간대별로 세부적으로 정의한 MAD-GAN을 발표하였다. 또한 Bashar and Nayak(2020)는 생성자를 이루는 LSTM의 은닉 노드 수를, 세 개의 층이 모두 동일한 GAN-AD 모델 구조에서 세 개의 층의 은닉 노드 수가 점차 증가하는 구조로 고도화된 TAnoGAN을 발표하였다. 이를 통해 GAN-AD보다는 생성자에서 다양한 압축 레벨(abstract level)로 데이터를 생성할 수 있게 하였다는 장점이 있다. GAN-AD, MAD-GAN, TAnoGAN 모두 한 층의 구분자 LSTM을 갖고 있어 특정 시계열 데이터에 대해 판별기에서 한 단계의 압축 레벨로 비교적 단순한 판단을 할 수밖에 없다는 한계점이 있다.
3. 제안 방법론
본 논문에서 제안하는WaDGAN-AD는 구분자와 생성자가 각각 LSTM으로 구성된 GAN 모델이다. 이처럼 구성한 이유는 GAN과 LSTM 모두 앞서 관련 연구에서 언급한 것처럼 시계열 데이터상에서 이상치를 탐지하는데 각자의 장점이 있기 때문이다. 우선 이상치 탐지에 GAN을 도입한 이유는 GAN을 구성하는 두 요소인 구분자와 생성자를 모두 이상치를 판단하는데 활용할 수 있기 때문이다. 구분자는 특정 객체의 분류 점수(likelihood)를 통해 정상과 이상을 판단할 수 있는 반면, 생성자는 생성자의 입력에 사용된 테스트 객체의 값과 해당 테스트 객체가 생성자에 의해 생성된 객체 값의 차이인 잔차를 활용하여 이상치 탐지를 할 수 있게 된다. 따라서 구분자와 생성자를 동시에 사용하여 해당 객체의 이상치 여부를 판단한다면 단순히 잔차 값으로 판단하는 LSTM-AE(Malhotra, Shroff, Agarwal, and Vig, 2015)보다 더욱 풍부한 정보력으로 이상치를 탐지할 수 있다는 장점이 있다. 반면, LSTM은 RNN의 기울기 소실의 단점을 해결하여 시계열 데이터에서 앞선 데이터의 정보를 망각하지 않는 학습을 수행하는 장점으로 인해 전력 소비량 데이터와 같이 긴 시간 동안 수집된 정보를 입력으로 사용하는 모델링 관점에서 유용한 구조가 될 수 있다.
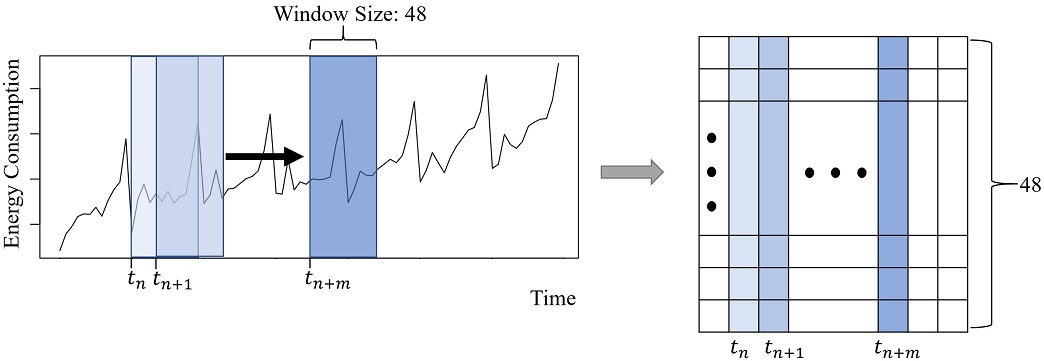
본 연구는 시계열 데이터를 여러 개의 윈도우로 분할하여 모델의 입력값으로 사용하는데 이는 분할된 윈도우가 하나의 단위가 되어 모델을 학습하거나 객체를 추론할 경우, 시계열 전체를 입력하는 경우보다 각 윈도우가 내포하고 있는 특징을 소실 없이 모델에 반영할 수 있기 때문이다. 본 연구에서는 <Figure 1>과 같이, 크기가 48인 윈도우를 설정하고 한 시점씩 윈도우가 이동하며 시계열 데이터를 여러 개의 데이터 단위로 나눈다. 48개의 시점을 갖는 데이터 단위를 하나의 입력 객체로 두어 학습, 검증 및 테스트를 진행한다.
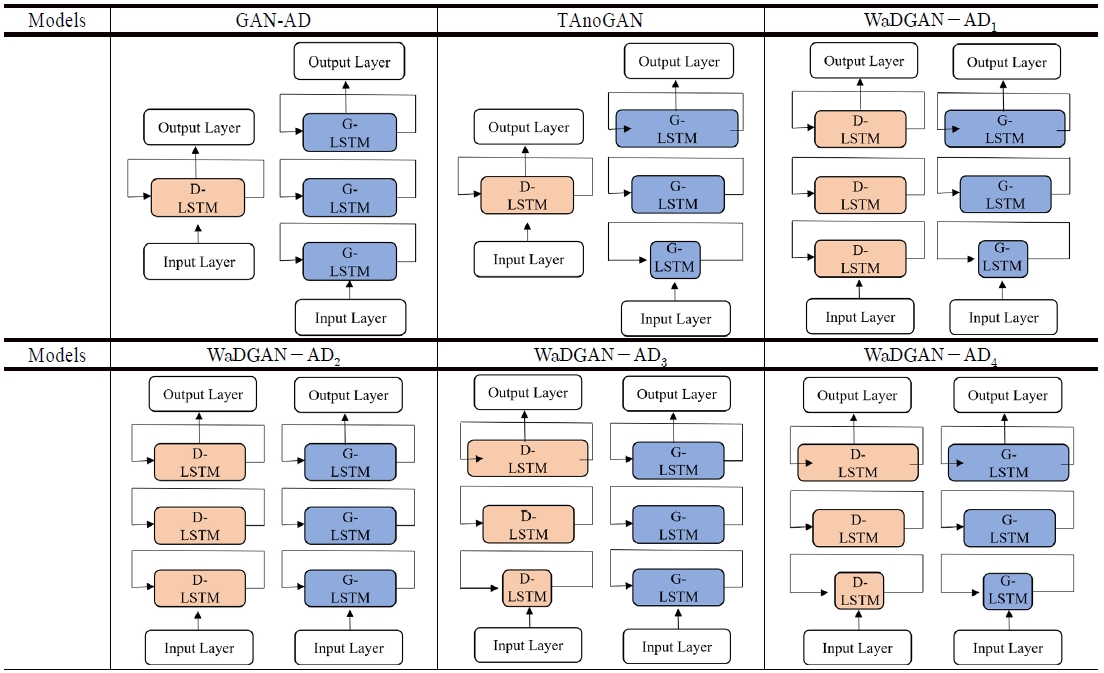
본 논문에서 제시하는 모델 WaDGAN-AD는 총 네 가지이며, GAN-AD나 TAnoGAN과 같이 LSTM과 GAN을 결합한 모델이지만 해당 구조에서 넓게(wider) 그리고 깊게(deeper) 구조를 변형한 모델이다. 이 두 가지 변형은 <Figure 2>와 같이 구분자의 LSTM이 갖는 은닉층을 하나의 층에서 세 개의 층으로 쌓는 ‘깊게(deeper)’ 만든 변형과 <Figure 3>과 같이 구분자 LSTM의 은닉 유닛 수를 층이 깊어질수록 점차 증가하는 형태로 구성한 ‘넓게(wider)’ 만든 변형이다. 이때 은닉 유닛 수는 첫 번째 층부터 각 64개, 64개, 64개에서 32개, 64개, 128개로 조정되었다.

Structure Change from One Layer of LSTM to Three Layers of LSTM (Left: LSTM with one hidden layer / Right: LSTM with three hidden layers)
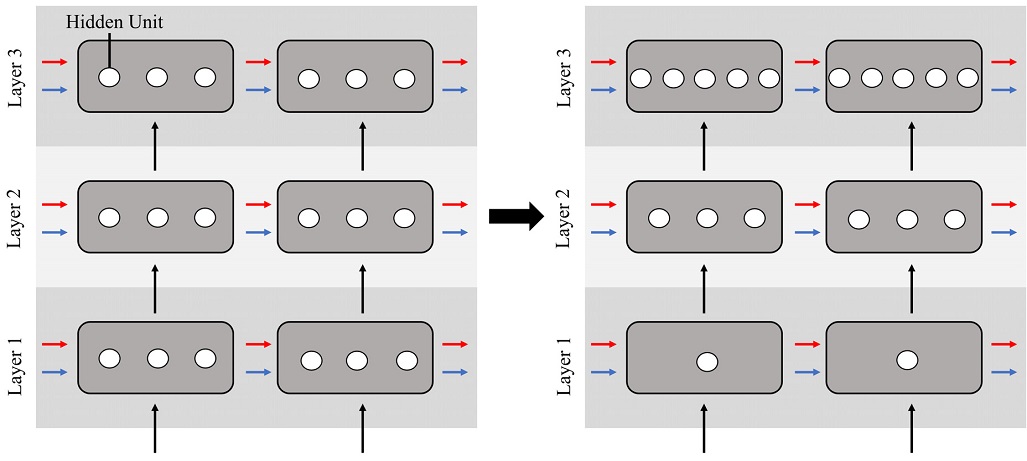
Structure Change from Layers with Same Number of Hidden Units to Different Numbers of Hidden Units (Left: LSTM layers with same number of hidden units / Right: LSTM layers with different numbers of hidden units)
<Figure 4>는 각 모델의 구분자 LSTM과 생성자 LSTM의 층 수와 각 층의 은닉 유닛 수를 간략한 형태로 표현하고 있다. 이때 LSTM의 블록이 한 개로 표현된 것은 해당 LSTM은 한 층으로 구성되어 있다는 의미이며 블록이 세 개로 표현된 것은 해당 LSTM은 세 개의 층으로 구성된 구조임을 의미한다. 또한, 각 LSTM의 은닉층의 블록의 너비가 동일한 경우에는 모든 은닉층의 은닉 유닛 수가 64개로 일정한 것이고 LSTM 블록의 너비가 일정하지 않고 증가하는 경우는 은닉 유닛 수가 32개, 64개, 128개로 증가하는 구조이다. WaDGAN-AD1는 세 층의 은닉 유닛 수가 일정한 구분자 LSTM과 세 층의 증가하는 은닉 유닛 수를 갖는 생성자 LSTM으로 이루어진 모델이다. 또한, WaDGAN-AD2는 세 층인 동시에 은닉 유닛 수가 모든 층에서 일정한 구분자 LSTM과 생성자 LSTM으로 이뤄진 모델이다. WaDGAN-AD3는 세 층의 은닉 유닛 수가 점차 증가하는 구분자 LSTM과 세 층의 일정한 은닉 유닛 수를 갖는 생성자 LSTM으로 이루어진 모델이다. 마지막으로 WaDGAN-AD4는 세 층이면서 은닉 유닛 수가 점차 증가하는 형태의 구분자 LSTM과 생성자 LSTM으로 이루어진 모델이다.
본 연구는 제시하는 모델 WaDGAN-AD가 선행 연구의 모델인 GAN-AD와 TAnoGAN보다 다음과 같은 이유로 우수한 이상치 탐지 성능을 나타낸 것으로 기대한다. 먼저 구분자 LSTM을 한 층에서 세 층으로 변경하게 되면 이전 층의 결과가 이후 층의 입력값으로 사용되면서 전력 시계열 데이터의 정교한 특성 표현을 도출할 수 있는 이유로 이상치 탐지 성능이 더 향상될 수 있다(Bashar and Nayak, 2020; Salman et al., 2018). 또한, 세 층의 구분자 LSTM의 은닉 유닛 수가 아래층부터 32, 64, 128개로 점차 증가하는 형태이면 짧은 주기부터 긴 주기까지 여러 주기를 포함하고 있는 시계열 데이터를 다양한 압축 레벨로 표현할 수 있으므로 현실에서 등장하는 대부분의 시계열 데이터와 같이 여러 주기성을 내포한 복잡한 데이터를 분석하기에 더욱 적합한 구조이다. 이러한 가정을 입증하기 위해 본 논문의 4장에서 세 개의 인공 데이터셋(synthetic dataset)으로 실험을 진행하였다.
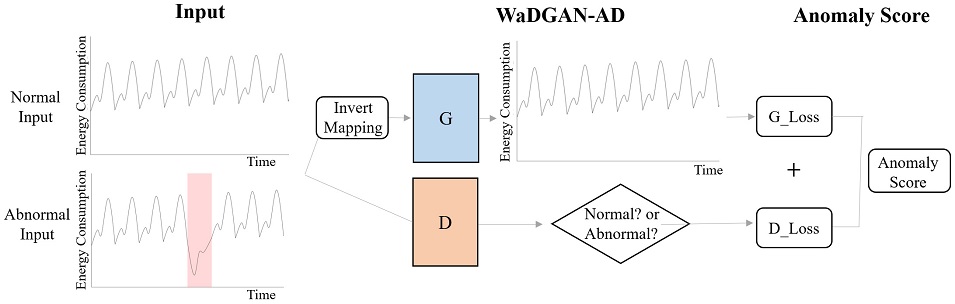
앞서 제안된 모델 구조는 모두 <Figure 5>와 같이 모델을 학습하는 과정과 이상 여부를 추론하는 과정으로 구성된다. 먼저 제안하는 모델은 비지도 학습 기반의 모델이므로 모델 학습 시 정상 시계열 데이터만을 사용한다. 기존 GAN의 원리와 동일하게 생성자는 입력 데이터와 매우 흡사하게 잠재 벡터로부터 적대적 샘플(adversarial sample)을 생성하는데, 이때 구분자가 정상 데이터와 적대적 샘플을 구별하지 못하게 하기 위해 해당 생성자는 정상적인 시계열 패턴과 매우 유사한 객체를 생성하도록 학습된다. 반면에, 구분자는 그럼에도 불구하고 노이즈(noise)가 추가된 적대적 샘플과 정상 데이터 객체를 정확하게 구분할 수 있도록 학습된다. 생성자와 구분자 간의 상호 학습으로 인해 각 구분자와 생성자 모두 정보 누락이나 지나친 일반화 없이 학습할 수 있다. 마지막으로 더 이상 구분자와 생성자의 파라미터가 업데이트되지 않을 때 학습을 중단한다.

Architecture of GAN and LSTM based Anomaly Detection Model. GAN-AD, TAnoGAN and WaDGAN-AD Share the Base Structure. The whole structure can be divided into model training phase and anomaly detector phase.
모델 학습 시 사용하는 구분자 손실과 생성자 손실(generator loss)은 다음과 같이 정의한다.
| (1) |
| (2) |
위 수식의 xi는 학습용 데이터 객체이고 zi는 각 xi에 상응하는 잠재 벡터이다. 수식의 D(xi)는 xi∈X(시계열 시퀀스)가 정상 데이터의 분포상에서 등장할 만한 확률값을 도출하는 함수로 xi가 정상 데이터 객체면 D(xi)의 값이 1에 가까운 수가 되는 반면 비정상적인 데이터 객체면 0에 가까운 수가 계산된다. 본 모델을 학습할 때는 식 (1)을 최소화하고 식 (2)를 최대화하는 방향으로 진행된다. 식 (1)을 최소화함으로써 xi에 대한 분류 점수가 최대화가 되고, 생성자에서 생성된 모조 데이터(fake data)에 대한 분류 점수는 최소화가 된다. 이를 통해 구분자는 실제 데이터와 모조 데이터를 명확하게 분류할 수 있게 된다. 반면에 식 (2)를 최대화함으로써 모조 데이터를 정상 데이터와 유사하게 생성하고자 하는 생성자의 의도를 반영하였다.
한편, 전력 소비량을 추론하는 단계는 <Figure 5>에서 볼 수 있듯이, 학습 단계에서 학습이 완료된 구분자와 생성자를 사용하여 데이터의 이상 여부를 추론한다. 이때, 테스트 데이터 객체(xi)에 해당하는 잠재 공간(latent space) Z상의 잠재 벡터를 찾고 다시 그 잠재 벡터와 생성자를 통해 입력된 시계열과 동일한 크기의 객체를 재구축한다. 대게 잠재 벡터로부터 그에 상응하는 객체를 생성하는 것은 가능하지만 역으로 데이터 객체가 주어졌을 때 이에 상응하는 잠재 벡터를 바로 도출하는 것은 불가능하다. 이에 본 연구에서는 도치 매핑을 사용하여 테스트 데이터 객체와 상응하는 잠재 벡터를 도출한다. 도치 매핑은 우선 잠재 공간상에서 임의의 잠재 벡터(z0)를 설정하고 해당 잠재 벡터로부터 생성된 데이터 객체()값과 원래의 입력 데이터 객체(xi)값을 차이를 구한다. 그리고 이 차이가 최소화되는 방향으로 잠재 벡터를 업데이트한다. 이때 업데이트를 하는 횟수는 하이퍼파라미터이며 본 연구에서는 50번의 업데이트를 진행하여 테스트 데이터 객체에 가장 상응하는 잠재 벡터를 구한다.
이러한 잠재 벡터를 사용하여 이상 여부를 추론하는 과정은 크게 구분자 이상치 점수(Dscore)와 생성자 이상치 점수(Gscore)로 나눌 수 있고 각 점수는 다음과 같이 표현한다.
| (3) |
| (4) |
| (5) |
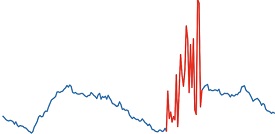
<Figure 6>과 같이 추론하고자 하는 데이터가 정상적일 경우, 본 모델은 정상 데이터로만 학습되었기 때문에 해당 데이터의 분류 점수와 (해당 데이터에 상응하는) 잠재 벡터를 생성자에 통과시켜 생성된 데이터의 분류 점수의 차이가 작다. 따라서 이 경우 식 (3)에 의해 구분자 이상치 점수는 낮은 값이 도출된다. 또한, 입력되는 정상 데이터와 생성자로 재구축된 데이터의 잔차가 적기 때문에 생성자 이상치 점수 역시 식 (4)에 의해 낮은 값을 갖게 된다. 반면에 추론하고자 하는 데이터가 비정상적일 경우, 해당 데이터의 분류 점수는 낮지만, 정상 데이터로 학습된 생성자에서 도출된 재구축된 데이터는 정상 데이터의 모습을 띠어 해당 분류 점수가 높으므로 두 값 사이의 괴리가 존재하며 구분자 이상치 점수 Dscore가 큰 값이 도출된다. 또한, 입력된 데이터는 비정상적 패턴을 갖지만, 재구축된 데이터는 생성자로 인해 정상적인 패턴을 띄므로 두 값 간의 잔차가 크고 결국 생성자 이상치 점수 Gscore도 높게 도출된다.
최종 이상치 점수는 식 (5)와 같이 테스트 데이터 객체의 구분자 점수와 생성자 점수를 가중 합하여 도출한다. 이때 식 (6)과 같이 특정 기준 값(τ)보다 이상치 점수가 크면 이상치로 판단되고, 기준값보다 작으면 정상 데이터로 판단한다. 이때, 가중 계수 λ와 기준값 τ는 하이퍼파라미터이다. 본 연구에서 λ는 0.1로 설정하였다.
| (6) |
4. 실험 및 결과
4.1 데이터셋 설명
본 연구는 제안하는 구조의 타당성을 입증하기 위해 세 개의 인공 데이터셋을 생성하였다. 인공 데이터셋 A는 주기가 1년인 데이터셋으로, 세 데이터셋 중 가장 단순한 특성을 갖는 데이터셋이다. 인공 데이터셋B는 인공 데이터셋 A보다 한 단계 더 특징이 가해진 데이터셋으로 연 단위의 주기와 주 단위의 주기가 포함된 데이터셋이다. 마지막으로 인공 데이터셋 C는 본 실험에서 사용한 실데이터셋인 대학 캠퍼스 데이터셋과 가장 유사하게 생성된 데이터셋이다. 해당 데이터셋은 연 단위, 주 단위, 일 단위의 세 가지 주기성을 모두 포함하고 있으며, 증가 혹은 감소 추세는 나타나지 않는 데이터셋이다. 식 (7)은 세 개의 인공 데이터셋 A, B, C를 생성할 때 활용되는 기초 식으로 Sn(t)는 한 개의 주기를 생성한다.
| (7) |
식 (7)의 λ는 노이즈의 강도(amplitude)로, MSCRED(Zhang et al., 2018)에서 적용한 인공 데이터셋 생성 시 적용한 값을 차용하여 0.3으로 설정하였다. β는 데이터셋이 음수가 되는 것을 방지하기 위해 더해주는 상수이며 본 연구에서는 이 값을 1로 설정하여 각 Sn(t)의 값의 최솟값이 0이 되게 하였다. 또, d는 시점의 변화가 발생할 경우를 반영하기 위해 도입된 상수이며 본 연구에서는 시간 지연 등 시점 변화에 대한 고려는 제외하였다. 마지막으로 wn은 각 Sn(t)의 주기를 표현할 때 사용하는 값이다. 따라서 일 년의 주기를 표현할 때의 w1는 4*24*365/2π의 값이고, 일주일의 주기를 표현할 때의 w2는 4*24*7/2π, 하루의 주기를 표현할 때의 w3는 4*24/2π가 된다. 따라서 Sn(t)는 시간 지연 및 시점 변화, 주기, 노이즈를 모두 고려한 수식이 된다.
세 개의 인공 데이터셋은 일 년, 일주일 또는 하루의 주기 정보 wn를 포함한 Sn(t)를 해당 주기 수만큼 더한 데이터셋이고 이는 로 표현할 수 있다. 이때 c의 값은 각 데이터셋이 갖고 있는 주기의 개수이다. 따라서 인공 데이터셋 A는 연 단위의 주기만 존재하는 데이터셋, B는 연 단위와 주 단위의 주기가 존재하는 데이터셋, C는 연 단위, 주 단위, 일 단위의 주기가 모두 존재하는 데이터셋이다. 각 데이터셋을 생성하는 식은 식 (8), 식 (9), 식 (10)에서 확인할 수 있으며 각 데이터셋에 포함된 주기는 <Table 1>에 나타나 있다.
| (8) |
| (9) |
| (10) |
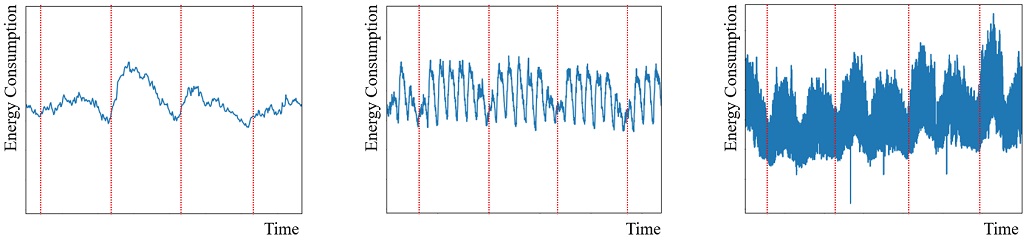
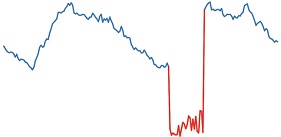
대학 캠퍼스 데이터셋은 2015년 1월 1일 0시 0분부터 2018년 12월 31일 23시 45분까지의 15분 단위로 수집된 국내 한 대학에 위치한 네 건물의 전력 소비량을 담은 시계열 데이터셋이다. <Figure 7>은 네 건물 중 한 곳의 전력 소비량을 보여주는 그림이며, 서로 다른 X축 범위를 통해 데이터셋이 하루 단위(좌측), 일주일 단위(중앙), 연 단위(우측)의 주기성을 모두 포함하는 것을 확인할 수 있다.
WaDGAN-AD는 비지도 학습을 기반으로 하는 모델이므로 정상 시계열 데이터로 모델을 학습한다. 반면에 검증 데이터와 테스트 데이터는 1%의 이상치가 존재하는 데이터를 사용하여 각각 하이퍼파라미터 값을 조정하며, 모델이 이상치를 탐지하는 성능을 평가한다.
이때, 이상치는 전력을 소비할 때 현실적으로 등장할 만한 세 개의 시나리오를 바탕으로 생성된 시계열 데이터이다. 첫 번째로 시나리오1은 전력 소비량을 기록하는 스마트 미터나 전력을 사용하는 기계 자체의 고장이 발생할 때, 전력 소비량이 급증하는 경우이다. 이 경우 이상치 구간의 각 데이터 포인트마다 6에서 10 사이의 무작위의 값을 곱하여 전력 사용량이 급증하는 것을 표현하였다. 또한, 시나리오2도 시나리오 1과 마찬가지로 고장이 발생한 경우이지만, 고장으로 인해 전력 소비량이 급감하는 경우이다. 그리고 해당 시나리오에 의거해 이상치 구간의 각 데이터 포인트마다 0.1에서 0.5 사이의 무작위의 값을 곱해주었다. 마지막으로 시나리오3은 사용자가 의도적으로 전력 소비량을 덜 소비한 것처럼 미터기 및 전력 네트워크를 조작하여 더 낮은 값을 지불하려는 경우이다. 이때는 이상치 구간의 각 데이터 포인트마다 0.1에서 0.8 사이의 무작위의 값을 곱하여 전력 소비가 의도적으로 급감한 것을 표현하였다. 이는 <Table 2>에서 원본 데이터와 각 시나리오에 해당하는 이상치 구간의 데이터를 비교할 수 있다. 또한, 세가지 시나리오를 토대로 대학 캠퍼스 데이터셋과 인공 데이터셋의 비정상적인 시계열을 모두 표현하였다.
각 모델의 학습 환경은 다음과 같다. 모델 학습 시 아담 옵티마이저(adam optimizer)에 기반한 미니배치 확률적 최적화(mini-batch stochastic optimization)와 경사 하강 최적화(gradient descent optimizer)가 사용되었으며 학습률은 0.01로 설정하였다. 전체 학습 에폭(epoch)은 20, 미니배치의 크기는 32를 사용하였으며, 최종 성능으로 5회 반복 실험의 평균값을 기재하였다. 또한, 실험은 Nvidia GeForce RTX 2080 ti BLOWER과 NVIDIA GeForce GTX TITAN X로 진행하였다. 해당 하이퍼파라미터와 GPU는 실데이터셋과 인공 데이터셋을 사용한 실험에 동일하게 적용되었다.
4.2 성능 평가 지표
본 연구에서 사용하는 모델들은 모두 정상 데이터만을 사용하여 학습하기 때문에, 테스트 단계에서 이상치 기준(cut-off)을 어떻게 설정하는가에 따라 테스트 객체의 이상치 여부가 달라진다. 따라서 가능한 모든 이상치 기준값에 따른 탐지율(true positive rate, TPR)과 오분류율(false positive rate, FPR)의 관계를 나타내는 ROC 곡선 아래의 넓이인 AUROC 값을 성능 평가 지표로 사용하였다.
4.3 실험 결과
본 연구에서 제안하는 WaDGAN-AD의 구조를 입증하기 위해 세 가지 인공 데이터셋으로 실험을 하였고, 그 결과는 <Table 3>과 같다. <Table 3>에서 각 데이터셋으로 실험한 결과 중 이상치를 탐지하는 성능이 가장 우수한 모델과 차등으로 우수한 모델이 모두 WaDGAN-AD임을 확인할 수 있다.
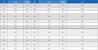
Anomaly detection results on synthetic datasets. Bold and underlined numbers indicate the best performance for each dataset. Bold numbers indicate the second-best performance for each dataset. Parentheses mean standard deviation. Experiments were conducted five times each.
또한, 구분자 LSTM을 1층에서 3층으로 변형하는 작업(deeper), 은닉 유닛 수를 증가하는 형태로 변형하는 작업(wider), 그리고 두 가지 변형을 통합한 작업(deeper and wider)의 각 효과를 파악하기 위해 <Table 3>의 결과로부터 <Table 4>를 도출하였다. <Table 4>는 세 가지 구조적인 변경 사항을 총 6가지의 경우로 두어, 각 경우에서의 AUROC의 상승 여부를 표현하고 있다. 이때 변경 전 모델은 <Table 4>의 From 부분, 변경 후 모델은 <Table 4>의 To 부분에서 확인할 수 있다. <Table 4>에 따르면 구분자 LSTM을 1층에서 3층으로 확장(deeper)한 결과, 2가지 모델 변화와 3가지 데이터셋에 대한 총 6가지 실험 모두 성능 향상을 보인 것을 확인할 수 있다. 또, 3층의 구분자 LSTM의 은닉 유닛 수를 일정한 수에서 층마다 다른 수로 변경(wider)했을 때, 인공 데이터셋 A는 성능이 향상되지 않았지만, 인공 데이터셋 B에서는 두 경우 중 한번, 인공 데이터셋 C에서는 모든 경우에서 이상치를 탐지하는 성능이 향상되었다. 마지막으로 구분자 LSTM을 1층에서 3층으로 쌓으며 3층의 은닉 유닛 수를 서로 다른 수로 구조를 변경했을 때(deeper and wider), 인공 데이터셋 A는 두 경우 중 한번, 인공 데이터셋 B와 C는 두 경우 모두 성능이 향상되었다.

Results indicating whether anomaly detecting performance has been improved. Circle indicates the performance has been improved and dash indicates it has not.
이와 같은 결과를 바탕으로 제안하는 방법론의 효과를 다음과 같이 해석할 수 있다. 우선 구분자 LSTM을 1층에서 3층으로 확장하였을 때, 시계열 데이터가 단순한 특성부터 여러 주기를 내포하고 있는 경우까지, LSTM의 이전 층의 결과가 그 이후 층의 입력값이 된다. 이때 적층 구조로 인해 이상치를 더욱 세밀하게 탐지할 수 있는 이유는 시계열 데이터에 존재하는 극소수의 이상치를 더욱 정교한 특성 표현(feature representation)으로 나타낼 수 있기 때문이다. 또한, 구분자 LSTM의 은닉 유닛 수를 32개, 64개, 128개로 두었을 때 시계열 데이터에 포함된 주기가 많을수록 성능이 향상되는 이유는 시계열 데이터를 다양한 압축 레벨로 표현할 수 있기 때문이다. 이는 짧은 주기부터 긴 주기까지 각 주기가 요구하는 은닉 유닛 수를 모두 포함할 수 있는 구조로써 2개 또는 3개의 여러 주기가 내포된 인공 데이터셋 B와 C로 실험할 때 성능이 향상되지만, 주기가 1개인 인공 데이터셋 A로 실험할 때는 효과적이지 않은 것으로 확인되었다.
대학 캠퍼스 건물별 전력 사용량 데이터셋으로 실험한 결과는 <Table 5>에서 확인할 수 있다. 실험에 사용된 네 개의 데이터셋 모두 일 년, 한 달, 하루의 주기가 모두 존재하는 데이터셋으로, 인공 데이터셋 C와 비슷한 특성을 갖는다. <Table 5>에 따르면 캠퍼스 건물 A를 제외한 세 개의 데이터셋이 GAN-AD와 TAnoGAN보다 네 개의 모델 WaDGAN-ADi (i = 1, 2, 3, 4)을 사용했을 때 평균적으로 성능이 향상되었다. 또한, 캠퍼스 건물 A의 두 번째로 높은 결과를 제외하면 본 연구에서 제안하는 WaDGAN-ADi(i = 1, 2, 3, 4)을 사용하였을 때 가장 높은 결과와 차등으로 높은 성능이 발생하는 것을 확인할 수 있다. (캠퍼스 건물 A의 경우, 기숙사 건물이며 기숙사 특성상 전력 소비량이 일 단위, 일주일 단위, 그리고 연 단위 모두 나머지 세 건물에 비해 비교적 불규칙적이다. 따라서 다른 건물의 데이터셋에 비해 모델의 구조를 완벽하게 반영하지 못하지 점이 존재한다.)

Anomaly detection results on campus datasets. Bold and underlined numbers indicate the best performance for each dataset. Bold numbers indicate the second-best performance for each dataset. Parentheses mean standard deviation. Experiments were conducted five times each.
대학 캠퍼스 건물 데이터셋 또한 <Table 5>의 이상치 탐지 결과로부터 <Table 6>을 생성하였다. <Table 6>에 따르면 우선 첫 번째 변형인 구분자 LSTM을 1층에서 3층으로 확장한 변형(deeper)을 가하면 총 8개 중 6개의 경우에서 성능이 향상된 것을 확인할 수 있다. 또한, 두 번째 변형인 구분자 LSTM의 세 층의 은닉 유닛 수를, 모두 일정한 형태에서 은닉 유닛의 개수가 점차 증가하는 구조로 변형하였을 때(wider), 총 8개 중 4개의 경우가 성능 향상을 보인 것을 알 수 있다. 마지막으로 구분자 LSTM을 넓고 깊게 만들었을 때(deeper and wider) 캠퍼스 건물 A를 제외한 나머지 세 개의 캠퍼스 건물들의 전력 소비량 이상치 탐지 성능이 모두 증가하는 것을 확인할 수 있다.
5. 결 론
본 연구는 전력 소비량 시계열 데이터에서의 이상치 탐지를 하기 위해 구분자 LSTM을 넓고(wider) 깊게(deeper) 만든 WaDGAN-AD를 제안하였다. ‘넓게’란 3층의 구분자 LSTM의 은닉 유닛 수를 일정한 숫자들로 이루는 것이 아닌 점점 증가하는 수들로 두는 것이고, ‘깊게’란 모델의 구분자 LSTM의 층을 1층에서 3층으로 증가시킨 형태를 일컫는다. 해당 모델로 실험한 결과, 일 년, 일주일, 그리고 하루 단위의 주기성을 모두 포함한 실제 캠퍼스의 네 개 건물의 데이터셋에서 WaDGAN-AD가 기존 방법론들보다 이상치 탐지를 더욱 우수하게 수행하는 것을 확인할 수 있다. 본 연구에서 제안한 방법론은 주기를 시계열 데이터의 성질로 특정하였다. 이 외 전력 소비량 시계열 데이터에서 발생할 수 있는 특성인 경향성 및 전력 네트워크상의 터뷸런스(turbulence) 등을 파악하여 이러한 특성을 포함한 시계열에서도 이상치를 탐지를 할 수 있는 연구를 진행하여 본 연구를 고도화하고자 한다.
Acknowledgments
이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(No.2021-0-00034, 파편화된 데이터의 적극 활용을 위한 시계열 기반 통합 플랫폼 기술 개발, No. 2021-0-00471, 모델링 & 최적화 기반 오류-free 정보인프라 자율제어 기술 개발)
References
-
Angelos, E. W. S., Saavedra, O. R., Cortés, O. A. C., and de Souza, A. N. (2011), Detection and Identification of Abnormalities in Customer Consumptions in Power Distribution Systems, IEEE Transactions on Power Delivery, 26(4), 2436-2442.
[https://doi.org/10.1109/TPWRD.2011.2161621]

- Audibert, J., Michiardi, P., Guyard, F., Marti, S., and Zuluaga, M. A. (2020), USAD: UnSupervised Anomaly Detection on Multivariate Time Series, In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 3395-3404.
-
Bashar, M. A. and Nayak, R. (2020). TAnoGAN: Time Series Anomaly Detection with Generative Adversarial Networks. In 2020 IEEE Symposium Series on Computational Intelligence (SSCI), 1778-1785.
[https://doi.org/10.1109/SSCI47803.2020.9308512]

-
Bynum, J. D., Claridge, D. E., and Curtin, J. M. (2012), Development and Testing of an Automated Building Commissioning Analysis Tool (ABCAT), Energy and Buildings, 55, 607-617.
[https://doi.org/10.1016/j.enbuild.2012.08.038]

-
Chandola, V., Banerjee, A., and Kumar, V. (2009), Anomaly Detection: A Survey, ACM Computing Surveys, 41(3), 1-58.
[https://doi.org/10.1145/1541880.1541882]

-
Chou, J. S. and Telaga, A. S. (2014), Real-time Detection of Anomalous Power Consumption, Renewable and Sustainable Energy Reviews, 33, 400-411.
[https://doi.org/10.1016/j.rser.2014.01.088]

-
Coma-Puig, B., Carmona, J., Gavalda, R., Alcoverro, S., and Martin, V. (2016), Fraud Detection in Energy Consumption: A Supervised Approach, In 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), 120-129.
[https://doi.org/10.1109/DSAA.2016.19]

- DataRPM, P. (2017), Anomaly Detection & Prediction Decoded: 6 Industries, Copious Challenges, Extraordinary Impact, Technical Report.
-
Dong, B., O’Neill, Z., and Li, Z. (2014), A BIM-enabled Information Infrastructure for Building Energy Fault Detection and Diagnostics, Automation in Construction, 44, 197-211.
[https://doi.org/10.1016/j.autcon.2014.04.007]

-
Fan, C., Xiao, F., Zhao, Y., and Wang, J. (2018), Analytical Investigation of Autoencoder-based Methods for Unsupervised Anomaly Detection in Building Energy Data, Applied Energy, 211, 1123-1135.
[https://doi.org/10.1016/j.apenergy.2017.12.005]

-
Hsieh, R. J., Chou, J., and Ho, C. H. (2019), Unsupervised Online Anomaly Detection on Multivariate Sensing Time Series Data for Smart Manufacturing, In 2019 IEEE 12th Conference on Service-Oriented Computing and Applications (SOCA), 90-97.
[https://doi.org/10.1109/SOCA.2019.00021]

-
Jiang, R., Lu, R., Wang, Y., Luo, J., Shen, C., and Shen, X. (2014), Energy-theft Detection Issues for Advanced Metering Infrastructure in Smart Grid, Tsinghua Science and Technology, 19(2), 105-120.
[https://doi.org/10.1109/TST.2014.6787363]

-
Jiang, W., Hong, Y., Zhou, B., He, X., and Cheng, C. (2019), A GAN-based Anomaly Detection Approach for Imbalanced Industrial Time Series, IEEE Access, 7, 143608-143619.
[https://doi.org/10.1109/ACCESS.2019.2944689]

- Kingman, D. P. and Ba, J. (2015), Adam: A Method for Stochastic Optimization, In 3rd International Conference for Learning Representations.
- Li, D., Chen, D., Goh, J., and Ng, S. K. (2018), Anomaly Detection with Generative Adversarial Networks for Multivariate Time Series, arXiv preprint, arXiv:1809.04758, .
-
Li, D., Chen, D., Jin, B., Shi, L., Goh, J., and Ng, S. K. (2019), MAD-GAN: Multivariate Anomaly Detection for Time Series Data with Generative Adversarial Networks, In International Conference on Artificial Neural Networks, 703-716.
[https://doi.org/10.1007/978-3-030-30490-4_56]

-
Li, X., Bowers, C. P., and Schnier, T. (2009), Classification of Energy Consumption in Buildings with Outlier Detection, IEEE Transactions on Industrial Electronics, 57(11), 3639-3644.
[https://doi.org/10.1109/TIE.2009.2027926]

- Malhotra, P., Vig, L., Shroff, G., and Agarwal, P. (2015), Long Short Term Memory Networks for Anomaly Detection in Time Series, In 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), 89-94.
-
McLaughlin, S., Podkuiko, D., and McDaniel, P. (2009), Energy Theft in the Advanced Metering Infrastructure, In International Workshop on Critical Information Infrastructures Security, 176-187.
[https://doi.org/10.1007/978-3-642-14379-3_15]

-
Pereira, J. and Silveira, M. (2018), Unsupervised Anomaly Detection in Energy Time Series Data Using Variational Recurrent Autoencoders with Attention, In 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), 1275-1282.
[https://doi.org/10.1109/ICMLA.2018.00207]

-
Qiu, H., Tu, Y., and Zhang, Y. (2018), Anomaly Detection for Power Consumption Patterns in Electricity Early Warning System, In 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI), 867-873.
[https://doi.org/10.1109/ICACI.2018.8377577]

- Radford, A., Metz, L., and Chintala, S. (2015), Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, arXiv preprint, arXiv:1511.06434, .
-
Ren, H., Hou, Z., and Etingov, P. (2018), Online Anomaly Detection Using Machine Learning and HPC for Power System Synchrophasor Measurements, In 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), 1-5.
[https://doi.org/10.1109/PMAPS.2018.8440495]

-
Salman, A. G., Heryadi, Y., Abdurahman, E., and Suparta, W. (2018), Single Layer & Multi-layer Long Short-term Memory (LSTM) Model with Intermediate Variables for Weather Forecasting, Procedia Computer Science, 135, 89-98.
[https://doi.org/10.1016/j.procs.2018.08.153]

-
Schuster, M. and Paliwal, K. K. (1997), Bidirectional Recurrent Neural Networks, IEEE transactions on Signal Processing, 45(11), 2673-2681.
[https://doi.org/10.1109/78.650093]

-
Weng, Y., Zhang, N., and Xia, C. (2018), Multi-agent-based UnsuperVised Detection of Energy Consumption Anomalies on Smart Campus, IEEE Access, 7, 2169-2178.
[https://doi.org/10.1109/ACCESS.2018.2886583]

- Wiggins, M. and Brodrick, J. (2012), HVAC Fault Detection, ASHRAE Journal, 54(2), 78-80.
-
Zhang, C., Song, D., Chen, Y., Feng, X., Lumezanu, C., Cheng, W., Ni, J., Zong, B., Chen, H., and Chawla, N. V. (2019), A Deep Neural Network for Unsupervised Anomaly Detection and Diagnosis in Multivariate Time Series Data, In Proceedings of the AAAI Conference on Artificial Intelligence, 33(1), 1409-1416.
[https://doi.org/10.1609/aaai.v33i01.33011409]

-
Zhang, Y., Chen, W., and Black, J. (2011), Anomaly Detection in Premise Energy Consumption Data, In 2011 IEEE Power and Energy Society General Meeting, 1-8.
[https://doi.org/10.1109/PES.2011.6039858]

-
Zheng, Z., Yang, Y., Niu, X., Dai, H. N., and Zhou, Y. (2017), Wide and Deep Convolutional Neural Networks for Electricity-theft Detection to Secure Smart Grids, IEEE Transactions on Industrial Informatics, 14(4), 1606-1615.
[https://doi.org/10.1109/TII.2017.2785963]

-
Zhu, G., Zhao, H., Liu, H., and Sun, H. (2019), A novel LSTM-GAN Algorithm for Time Series Anomaly Detection, In 2019 Prognostics and System Health Management Conference (PHM-Qingdao), 1-6.
[https://doi.org/10.1109/PHM-Qingdao46334.2019.8942842]

Appendix
<부 록> 기존 모델과의 추가 비교
본 연구는 WaDGAN-AD의 깊고(deeper) 넓은(wider)한 구조의 영향을 파악하기 위해 GAN-AD, TAnoGAN과 비교하여 실험하였다. 또한 GAN을 도입한 효과를 입증하기 위해 오토인코더 모델과 LSTM을 결합한 LSTM-AE1, LSTM-AE3, BiLSTM-AE(Schuster and Paliwal, 1997)와의 비교 실험을 하였다. 이때 LSTM-AE1는 은닉 층의 개수가 1개, LSTM-AE3는 은닉 층의 개수가 3개, BiLSTM-AE는 은닉 층의 개수가 3개인 양방향 LSTM이다. 실험 결과는 <Table 7>에서 확인할 수 있다. <Table 7>에 따르면 GAN을 도입한 WaDGAN-AD와 GAN을 도입하지 않은 그 외의 모델의 AUROC의 차이가 0.2 이상임을 알 수 있다. 이로 인해 GAN의 생성자와 구분자간의 상호 작용으로 작동되는 구조를 통해 시계열상에 존재하는 이상치를 더욱 세밀하게 탐지하는 것을 알 수 있다.
김혜연 : 고려대학교 산업경영공학부에서 2020년 학사학위를 취득하였다. 현재는 고려대학교 산업경영공학부에서 석사과정으로 재학 중이다. 연구 분야는 비지도 학습 기반의 이상치 탐지이다.
김형석 : 단국대학교 정보통계학과에서 2015년 학사학위를 취득하였다. 현재는 고려대학교 산업경영공학부 석박통합과정으로 재학 중이다. 주 연구분야는 이상치 탐지 및 딥러닝 기반의 그래프 방법론이다.
강필성 : 서울대학교 산업공학과에서 2003년 학사, 2010년 박사학위를 취득하였다. 이후 현대카드 과장, 서울과학기술대학교 조교수로 근무하였으며, 현재는 고려대학교 산업경영공학부 부교수로 재직 중이다. 연구 분야는 정형 및 비정형 데이터를 활용한 데이터마이닝 및 기계학습 알고리즘 개발 및 제조/IT/공공분야 응용이다.