상관관계 분석 및 데이터 증강을 활용한 반도체 설비 고장 감지
© 2024 KIIE
Abstract
Traditional control charts and machine learning methods have been used to detect equipment failures in semiconductor processes. However, detecting failures and identifying their root causes can be challenging because of the complexity of the process and structural characteristics of the equipment. Moreover, the anomaly sections for each part can be imbalanced, which can hinder classification performance. In this study, we propose a method to detect failures using the correlation of variables and data augmentation. The proposed method consists of five steps: (1) conversion of the multivariate time series data of the equipment into signature matrices, (2) detection of anomalies using a convolutional autoencoder, (3) augmenting the number of residual matrices of minority classes (4) learning convolutional neural network that use the residual matrixes of definite abnormal sections, and (5) application of Grad-CAM to interpret the convolutional neural network. We demonstrate the effectiveness and applicability of the proposed method using real-world multivariate time series data obtained from ashing process equipment in semiconductor manufacturing.
Keywords:
Anomaly Detection, Data Augmentation, Explainable Artificial Intelligence, Multivariate Time Series Data, Semiconductor Equipment1. 서 론
반도체 산업은 가전기기의 발전과 스마트폰의 등장으로 중요성이 지속적으로 상승해왔다. 현재는 반도체가 인공지능 발전의핵심적인 역할을 하고 있기 때문에 미래 수요를 충족하기 위해 반도체 생산성 향상이 필수적이다(Yoon et al., 2021). 더불어, 반도체 크기가 미세화되면서 설비의 미세한 변화도 제품에 영향을 미치게 되어 생산성과 품질을 유지하는 것이 더욱 어려워졌다(Chien et al., 2011). 이에 따라, 공정 설비의 상태를 정확하게 진단하고 분석하는 것이 매우 중요해졌다.
현재 반도체 산업에서 설비 고장 및 오류를 감지하기 위해 FDC(fault detection and classification) 시스템을 사용하고 있다. FDC 시스템은 실시간으로 설비 센서 데이터(온도, 압력, 전력 등)를 수집하고 각 센서 데이터를 단변량 차트로 변환하여 이상을감지하는 시스템이다. 공정별 설비 엔지니어들이 직접 임계값을 설정하고, 특정 센서가 정해진 임계값을 벗어나면 해당 센서 데이터에 인터락(interlock)이 걸리게 된다. 여기서 인터락이란 설비 동작을 특정 조건에서 정지시키기 위한 장치 또는 시스템을 의미한다. 설비 엔지니어들은 FDC 시스템을 활용하여 인터락이 걸리게 되면 설비 이상 유무를 판단하고 점검해야 할 부분을 결정하게 된다.
이에 따라, 전통적으로 슈왈츠 제어 차트(Shewhart control chart), 누적합 제어 차트(cumulative sum control chart, CUSUM), 지수 가중 이동 평균 차트(exponentially weighted moving average chart, EWMA) 등 단변량 차트를 사용하여 반도체 설비 고장을 감지하기 위한 연구들이 진행되었다(Awais et al., 2018; Liu et al., 2023; Raji et al., 2020). 하지만, 해당 연구들은 변수 간 상관관계 변화를 반영하지 않기 때문에 비정상적인 이상 징후를 제대로 탐지하는 데 한계가 존재한다. 따라서 단변량 접근 방법만으로 반도체 설비의 고장을 감지하고 원인을 파악하는 것은 잘못된 경보를 발생시킬 수 있다(Chien et al., 2013; Thieullen et al, 2013). 반도체 설비는 압력, 온도, 전력 등 여러 가지 요소들이 서로 조합되어 공정이 이루어지기 때문에 설비 내 센서 데이터 간 상호관계성을 가지고 있다. 따라서 단변량만으로 고장을 감지하는 것은 오류를 범할 수 있다(He et al., 2007 Kourti et al., 1995).
이에 따라, 최근 반도체 산업에서는 다변량 데이터를 적용하여 고장을 탐지하는 알고리즘 연구에 관심이 높아지고 있다. 하지만, 반도체 산업과 같은 제조 산업에서 수집되는 데이터에는 정상 데이터가 많고, 비정상 데이터가 적은 불균형 데이터 구조를 갖고 있다(Michau et al., 2020). 이러한 비정상데이터가 적은 상황을 해결하기 위해 정상 데이터만으로 모델을 학습 시켜 이상 탐지를 예측하는 연구가 많이 진행되었다(Pang et al., 2021). 따라서, 정상 데이터 샘플과의 차이를 통해 이상을 판별하는 LOF(local outlier factor), k-최근접이웃(k-nearest neighbor, KNN), 서포트 벡터 머신(support vector machine, SVM) 그리고 단일 클래스 서포트 벡터 머신(one class support vector machine, OCSVM)과 같은 모델들이 사용되었다(Cho et al., 2012; He et al., 2007; Park et al., 2010; Susto et al., 2017). 또한, 입력 데이터를 압축한 후 복원하여 이상치를 탐지하는 오토인코더(autoencoder) 신경망 기반 모델들이 사용되었다(Hosseinpour et al.,2022; Liao et al., 2018). 기존 연구들은 설비 센서 데이터를 사용하여 높은 이상 탐지 성능을 보여주었지만, 원시(raw) 데이터를 입력으로 사용하였기 때문에 변수 간 관계를 충분히 고려하지 못하였고, 결과에 대한 명확한 해석을 제공하지 못하였다. 따라서 기존 제안된 방법들은 다변량 데이터 변수 간 관계를 해석하는데 어려움이 있다는 한계를 가지고 있다(Ruff et al., 2021).
본 연구에서는 반도체 에싱(ashing)공정 설비 다변량 센서 데이터를 활용하여 설비 이상을 탐지하고, 비정상 구간에서 교체가 필요한 부품을 예측하며, 이와 관련된 주요 변수를 파악하는 방법을 제안한다. 본 논문의 기여점은 다음과 같다.
- (1) 반도체 설비 다변량 센서 데이터 변수 간 관계성 및 패턴을 명확히 반영하고 효과적으로 분석하기 위해 특징 행렬(signature matrix)을 적용하여 설비 이상 여부를 검출하였다.
- (2) 설비 이상 구간에서 발생하는 잔차 행렬(residual matrix)을 사용하여 교체가 필요한 부품을 예측하였다. 이때, 불균형하게 발생한 잔차 행렬 수를 보완하기 위해 데이터 증강 기법을 적용하여 분류 모델 성능을 향상시켰다.
- (3) 분류 모델을 해석하기 위해 Grad-CAM을 적용하였고, 부품 예측 시 잔차 행렬 내 어떤 부분을 고려하는지 확인함으로써, 고장 부품과 관련된 주요 변수를 시각적으로 파악하여 다변량 데이터 변수 간 관계를 해석하고 예측 결과 설명력을 향상시켰다.
본 논문의 구성은 다음과 같다. 제2장에서는 반도체 산업에서 이상 탐지를 실시한 관련 연구들을 소개하고, 제3장에서는 제안 방법론에 대하여 자세히 설명한다. 제4장에서는 실험 결과를 살펴본다. 제5장에서는 본 연구의 결론과 기대 효과에 대해 다룬다.
2. 관련 연구
반도체 제조 공정은 복잡성과 민감성으로 인해, 이상 징후를 조기에 탐지하고 대응하는 것이 매우 중요하다. 특히, 반도체 제조 공정에서 이상 징후를 탐지하는 것은 불량 생산을 최소화하고 설비 고장을 예방하는 데 핵심적인 역할을 한다. 따라서, 반도체 산업에서 이상을 탐지하기 위한 다양한 연구들이 진행되었다. 전통적으로는 단변량 데이터 분석에 초점을 맞춘 이상 탐지 연구들이 진행되었다. Jeong et al.(2013)은 웨이블릿(wavelet) 영역에서 공정 이상 감지를 위한 유의미한 계수를 추출하고 지수 가중 이동 평균을 적용하여 플라즈마 에칭 공정(plasma etching process) 설비 이상을 감지하였다. Awais et al.(2018)은 포토리소그래피(photolithography) 공정 중 하드 베이크(hard bake) 공정에서 발생하는 데이터를 사용하여 웨이퍼 흐름 폭 이상을 감지하기 위해 누적합 제어 차트를 적용하였고, Raji et al.(2020)은 모집단의 분포를 가정하지 않고 이상을 탐지하기 위해 비모수 슈왈츠 제어 차트를 적용하여 하드 베이크 공정 이상을 감지하였다. Liu et al.(2023)은 이상 탐지 결과에 대한 불확실성을 줄이기 위해 베이지안 적응형 지수 가중 이동 평균 제어 차트를 적용하여 하드 베이크 공정 이상을 감지하였다. 이러한 단변량 접근 방식은 개별 센서 데이터나 특정 공정 변수에 독립적으로 집중하여 이상 상태를 탐지하려고 하였다. 하지만, 이 방법들은 다변량 데이터에서 변수 간 상호작용이나 연관성을 반영하는 데는 한계가 있었다. 반도체 제조 공정은 여러 변수들이 서로 복잡하게 연관되어 있으며, 이러한 상호작용은 전반적인 공정 안정성과 품질에 영향을 미친다. 따라서, 다양한 공정 요소 관계성을 고려하여 이상을 탐지하는 다변량 데이터 분석 방법이 더욱 중요해졌다.
이에 따라, He et al.(2007)은 반도체 에칭 공정 설비 다변량 센서 데이터를 이용하여 k-최근접이웃 모델을 적용하였다. 정상 데이터만으로 이루어진 학습 데이터 샘플과 유사성을 기반으로 거리가 기준값보다 멀 경우 비정상으로 판단하여 반도체 설비 이상을 감지하였다. Park et al.(2010)은 화학 증착 공정(chemical vapor deposition) 설비의 정상 데이터로 서포트 벡터 머신을 학습하고 예측값과 실제 값 차이를 비교하여 이상을 탐지하였고, Cho et al.(2012)은 정상 데이터 영역을 더욱 정확하게하기 위해 단일 클래스 서포트 벡터 머신을 적용하여 화학 증착 공정 설비 이상을 탐지하였다. Thieullen et al.(2013)은 주성분 분석(principal component analysis) 모델을 사용하여 화학 증착 공정 설비에서 수집된 데이터를 분석하고 지수 가중 이동 평균을 사용하여 반도체 설비 이상을 탐지하였다. Susto et al.(2017)은 에칭 공정 다변량 센서 데이터의 정상 데이터만으로 LOF 모델을 학습하고 주변 데이터 포인트들과의 밀도를 고려하여 이상을 탐지하였다. Jahan et al.(2021)은 반도체 클린 룸(clean room) 내부 입자 레벨 측정 센서 데이터를 사용하여iForest(isolation forest) 모델을 학습하고 웨이퍼 결함을 탐지 및 클린 룸 내부 이상을 탐지하였다. 이러한 이상 탐지를 위한 머신러닝 알고리즘들은 반도체 설비 다변량 데이터 패턴을 분석하고 효과적인 이상 탐지 결과를 보여주었다. 하지만, 반도체 제조 공정 복잡성과 데이터의 다양성을 고려할 때, 방대한 데이터양을 효율적으로 처리하고 더욱 세밀한 패턴 인식과 예측 능력을 갖춘 딥러닝과 신경망 기반 접근 방법이 필요해졌다. 따라서, 복잡한 데이터 구조와 패턴을 학습하고, 시계열 데이터의 시간 변화 특성과 같은 추가적인 요소들을 고려하기 위해 딥러닝 방법을 적용하였다.
Liao et al.(2018)은 화학 증착 공정 설비 센서 데이터에 시간-주파수(time-frequency) 분석을 적용하고 적층형 오토인코더(stacked auto encoder) 모델을 학습하여 설비 이상을 탐지하였다. Zhanget al.(2020)은 합성곱 오토인코더 (convolutional autoencoder)와 k-최근접이웃을 결합한 이상 탐지 방법을 제안하였다. 에칭 공정의 정상 데이터 세트를 활용하여 합성곱 오토인코더를 학습하고 특징을 추출한 후, k-최근접이웃을 이용하여 새로운 데이터 특징과 정상 데이터 특징 사이의 거리를 계산하여 비정상 데이터를 식별하였다. Yong et al. (2020)은 에칭 공정에서 발생하는 설비 센서 데이터를 수집하여 합성곱 신경망(convolutional neural network)과 변분 오토인코더(variational autoencoder)를 결합한 모델을 사용하여 설비 이상을 감지하였다. 이러한 발전에 이어, 반도체 공정 데이터의 시간 특성을 분석함으로써, 이상 탐지 정확도를 높이고자 하였다. Kim et al.(2017)은 반도체 제조 공정에서 발생하는 설비 이상을 탐지하기 위해 시계열 데이터 시간 순서와 패턴을 학습하고 장기 의존성을 처리할 수 있는 LSTM 오토인코더(long short term memory autoencoder) 모델을 적용하였고, Hosseinpour et al.(2022)은 반도체 플라즈마 에칭 설비 센서 데이터에LSTM 오토인코더를 적용하여 불량 웨이퍼를 검출하였다. Tchatchoua et al.(2022)은 시간에 따른 데이터의 복잡한 특성과 신호 변동성을 효과적으로 분석하고 처리할 수 있는 1D-ResNet(residual network) 구조를 사용하였으며, 플라즈마 에칭 설비 데이터를 활용하여반도체 제조 공정의 고장을 감지하고 불량 웨이퍼를 분류하였다. 하지만 시간 종속성을 고려하는방법은 입력 데이터에 노이즈(noise)가 많은 경우 성능에 부정적인영향을 미칠 수 있다. 따라서, 노이즈가 많은 데이터의 경우, 노이즈 제거 오토인코더(denoising autoencoder)를 이용한 이상 탐지 방법이 연구되었다. Lee et al.(2016)은 포토리소그래피 공정 데이터에 대해 적층형 노이즈 제거 오토인코더(stacked denoising autoencoder)를 사용하여 설비 이상을 감지하고 불량 웨이퍼를 탐지했다. Jang et al.(2019)은 에칭 및 화학 증착 공정 데이터의 정상 데이터만으로 노이즈 제거 오토인코더를 학습하고, 비정상 데이터 입력 시 노이즈를 완벽히 제거하지 못해서 발생하는 잔류 노이즈를 통해 설비 이상을 탐지하였다. 또한, Fan et al.(2020)은 반도체 박막 증착 공정 데이터를 사용하여 설비 이상과 웨이퍼 결함을 검출하기 위해 노이즈 제거 오토인코더를 사용하였다. 하지만 해당 연구들은 주로 원시 데이터를 직접적으로 활용함으로써, 공정 변수들 간 복잡한 상호작용과 연관성을 충분히 파악하는데 한계를 보였다. 또한, 이들 연구는 결과 해석 가능성에 대해 충분한 정보를 제공하지 못했으며, 이는 실제 공정에서 발생할 수 있는 다양한 이상 징후를 정확히 탐지하고 이해하는 데 한계를 가져왔다. 이에 본 연구는 반도체 공정 설비 다변량 시계열 데이터 변수들 간 상관관계를 고려한 향상된 입력 방식을 적용한다. 이를 통해 보다 정교한 이상 탐지를 수행하고, 고장이 발생한 부품 예측 및 공정에 영향을 미치는 주요 변수들을 식별하여 이상 탐지뿐만 아니라 원인을 해석하는 연구를 제안한다.
3. 제안 방법론
본 연구에서 제안하는 방법의 전체 구조는 <Figure 1>과 같다. 반도체 설비로부터 생성되는 다변량 시계열 데이터를 특징 행렬(signature matrix)로 변환하고 특징 행렬을 합성곱 오토인코더(convolutional autoencoder)의 입력으로 사용하여 이상 탐지를 실시한다. 다음으로, 확실한 이상 구간에서 생성된 잔차 행렬(residual matrix)을 기반으로 합성곱 신경망을 통해 분류 작업을 수행하여 교체 부품을 예측한다. 이때, 이상 구간별 잔차 행렬의 불균형을 해결하기 위해서 소수 클래스(minority class) 데이터를 증강하여 분류 성능을 향상시킨다. 마지막으로 Grad-CAM을 사용하여 교체 부품 예측과 관련된 주요 요인을 파악한다.
3.1 다변량 시계열 데이터의 특징 행렬 변환
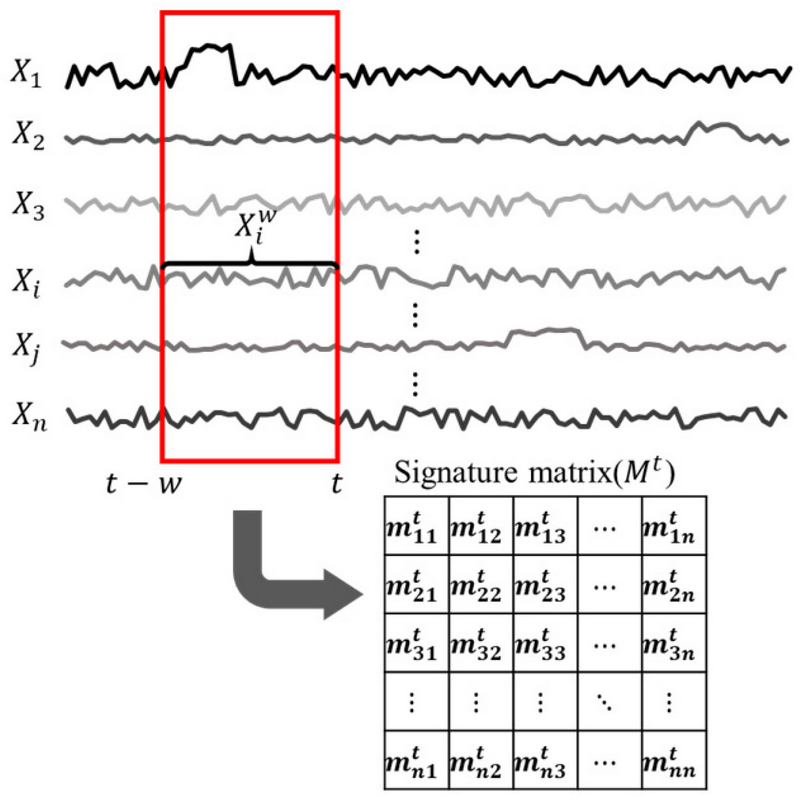
반도체 공정 설비에서는 다변량 센서 데이터가 수집되며, 구조적 특징으로 인하여 센서 데이터 변수 간 상호 연관성을 고려해야 한다. 또한 실제 산업에서 센서 데이터에는 노이즈가 포함되어 있기 때문에 이에 대한 강건함이 필요하다. Zhang et al.(2019)은 노이즈가 있는 다변량 시계열 데이터를 처리하고 변수들간 관계성을 반영하기 위해 특징 행렬(signature matrix)을 제안했다. 이때, signature라는 용어는 어떤 것의 특성을 나타내는 것을 의미하기 때문에, 특징 행렬(signature matrix)은 시계열 데이터 간 상관관계를 표현하는 행렬을 의미한다. <Figure 2>는 다변량 시계열 데이터를 특징 행렬로 변환하는 예시이다.
Xi는 n개의 다변량 시계열 데이터 중 i번째 시계열 데이터이며, 는 i번째 시계열 데이터 안에서 time window(t-w시점부터 t시점까지) 구간을 나타낸다. 두 개의 시계열 데이터 와 를 고려할 때, 두 시계열 데이터를 내적 연산 하여 특징 행렬의 성분 을 구성한다. 구체적인 수식은 식 (1)과 같다.
| (1) |
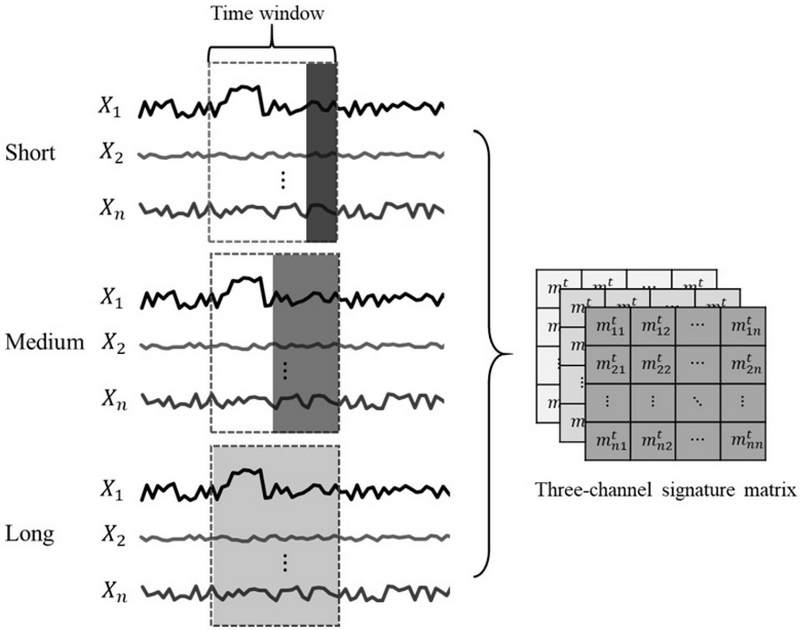
여기서, w는 time window 크기를 의미하며, k는 재조정 요소(rescale factor, k=w)로써 성분 값이 time window 크기에 따라 과도하게 변동하는 것을 방지하고, 일관된 기준으로 정규화 되도록 한다. 식 (1)의 내적 연산을 통해 t시점에서의 n×n 행렬 Mt을 생성한다. 추가적으로 하나의 time window 안에서 다양한 특징을 추출하기 위해 짧은 구간(short), 중간 구간(medium), 긴 구간(long)으로 나누어 n×n×3의 3채널(channel) 행렬을 생성한다. <Figure 3>은 time window 안에서 3채널 행렬을 구성하는 예시를 보여준다. 본 연구에서 정의한 짧은 구간, 중간 구간, 긴 구간 크기는 각각 25, 50, 100이다.
3.2 합성곱 오토인코더 기반 이상 탐지
Time window가 이동하면서 다변량 시계열 데이터는 특징 행렬로 변환된다. 이때, time window 안에 비정상 데이터가 포함되면 해당 time window는 비정상으로 레이블(label)이 지정된다. 하지만, 이것이 확실한 비정상인지 판단을 할 필요가 있다. 만약 time window 내 정상 데이터 99%와 비정상 데이터 1%가 포함된다면 해당 time window는 비정상으로 레이블이 지정될 것이다. 하지만 해당 time window가 비정상으로 레이블이 지정되더라도 정상 데이터가 99%로 상당히 높은 비율을 차지하고 있기 때문에 정상 데이터 특징을 많이 포함하고 있다. 이는 비정상 구간별 데이터 특징을 활용하여 고장 부품을 예측하는 분류 단계에서 예측 정확성을 저하시킬 수 있다. 이에 따라 확실한 비정상인지 추가적인 판단을 실시하여 보다 신뢰성 있는 비정상을 판단하고 부품 분류 단계에서 확실한 비정상 구간에서 생성된 잔차 행렬만을 사용하기 위해 이상 탐지를 수행한다.
오토인코더는 비지도 이상 탐지 분야에 주로 활용되며 우수한 성능을 보이고 있는 알고리즘이다(Chen et al., 2018). 데이터를 효과적으로 재구성하는 작업에서 재구성 오차(reconstruction error)를 통해 이상을 감지하고, 데이터의 잠재적인 패턴을 학습하여 이상 데이터를 식별한다. 합성곱 오토인코더는 오토인코더의 구조를 합성곱 구조로 변형한 것으로 주로 행렬 형태의 입력 데이터를 처리하며 공간적 패턴과 특징을 감지하는 데 우수한 성능을 나타낸다(Azarang et al., 2019 David et al., 2016). 본 연구에서는 이상 탐지를 실시하기 위해 특징 행렬을 입력으로 사용하는 합성곱 오토인코더를 통한 이상 탐지를 실시한다.
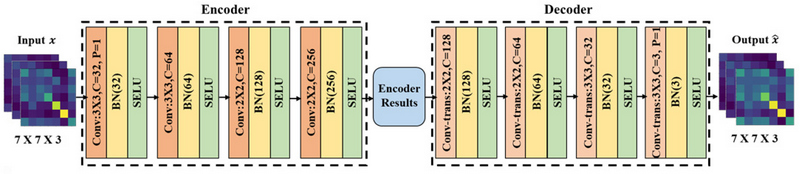
<Figure 4>는 사용한 합성곱 오토인코더의 구조를 나타낸다. 입력은 3채널 특징 행렬을 사용하였다. Conv는 합성곱 층을 나타내며, 3×3과 2×2는 커널(kernel) 크기가 각각 3과 2임을 의미한다. C와 P는 출력 채널의 수와 패딩(padding) 크기를 의미한다. 보폭(stride)은 1로 설정하였다. 합성곱 오토인코더의 인코더(encoder)와 디코더(decoder)는 모두 4개의 층으로 구성되며, 각 층은 합성곱 후 배치 노름(batchnorm, BN)과 활성화 함수 구조로 구성하였다. 활성화 함수는 SELU(scaled exponential linear units)를 사용하였다(Klambauer et al., 2017). SELU는 자기 조절 신경망(self-regulating neural network)을 활성화하여 오토인코더의 정확도를 향상시키고 복잡한 정규화 기술의 필요성을 줄일 수 있으며, 수렴 속도 측면에서도 다른 활성화 함수들보다 우수한 것으로 알려져 있다(Kuchaiev et al., 2017; Tomar, 2022). 합성곱 오토인코더는 입력 데이터와 출력 데이터간 차이를 최소화하는 방향으로 학습을 하며, 손실 함수식은 식 (2)와 같다.
| (2) |
여기서 x는 입력 행렬 성분, 는 출력 행렬 성분을 나타낸다. c는 채널을 의미하며, F는 프로베니우스 노름(frobenius norm)으로 행렬의 각 성분 별 유클리디안(Euclidean) 거리이다. 정상 데이터만으로 이루어진 특징 행렬을 입력으로 사용하여 합성곱 오토인코더가 학습되고, 비정상 데이터가 포함된 특징 행렬이 입력되면 정상적으로 재구축 하지 못하기 때문에 입력 데이터와 출력 데이터 간 차이가 커지게 된다. 입력 데이터와 출력 데이터 간 차이를 이상치 점수로 정의하며 합성곱 오토인코더는 이상치 점수를 기준으로 이상 탐지를 실시한다.
본 연구에서 이상치 점수는 잔차 행렬 성분 중 특정 임계값 δ을 초과하는 행렬 성분 개수로 계산된다. δ는 재구성 오차값들의 평균으로 결정되며, 잔차 행렬은 재구성 오차로 구성된다. 즉, 잔차 행렬은 입력 데이터와 출력 데이터 차이의 제곱으로 생성되며, 잔차 행렬 성분 값이 크다는 것은 해당 성분을 구성하는 데이터가 정상 상태와 다르다는 것을 의미한다. 따라서 잔차 행렬 성분 개수를 이상치 점수로 설정하여 이상 탐지를 할 수 있다. 그리고 이상치 점수가 임계값 τ를 초과하면 비정상으로 간주한다. τ는 정상 데이터만으로 구성된 검증 데이터 이상치 점수 평균값으로 설정하며 해당 수식은 식 (3)과 같다.
| (3) |
여기서 score(t)valid는 검증 데이터 이상치 점수이고, F1 점수가 최대가 되도록 1과 2 사이의 α 값을 결정한다(Zhang et al., 2019). <Table 1>은 α 값을 변경하였을 때 성능을 보여주며 F1 점수가 최대가 되는 α 값을 확인하였다. 이를 바탕으로 본 연구에서는 α 값을 1.7로 설정하였다.
3.3 합성곱 신경망 기반 고장 부품 분류
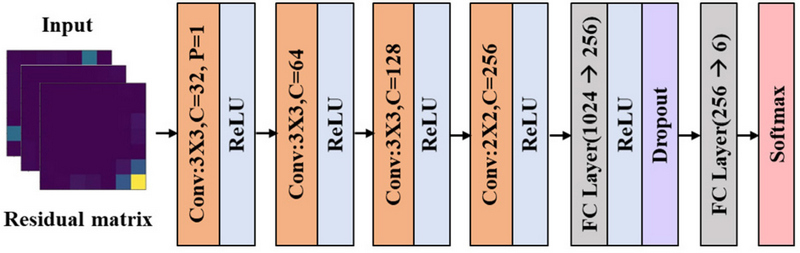
이상 탐지 후 확실한 이상으로 판정된 구간에서 생성되는 잔차 행렬은 비정상 데이터 특징 및 패턴을 정량화하고 있기 때문에 잔차 행렬을 입력으로 사용할 경우 분류 모델이 이상 구간별 특징에 집중하여 학습할 수 있게 된다. 따라서, 이를 합성곱 신경망 입력으로 사용하여, 이상 구간에서 교체해야 할 부품을 예측한다. 이때, 비정상 구간별 설정되어 있는 부품 레이블을 출력으로 사용하여 지도 학습 방식으로 모델을 학습하고 예측한다. <Figure 5>는 합성곱 신경망(convolutional neural network) 구조를 나타낸다. 합성곱 신경망 구조는 총 6개 층으로 구성되며 합성곱 층 4개와 완전 연결 층(fully connected layer, FC Layer) 2개로 구성된다. 첫 번째 완전 연결 층에는 드롭아웃(dropout)을 적용하고 활성화 함수는 ReLU(rectified linear unit)를 사용하였다. 마지막 층에는 소프트맥스(softmax)를 적용하여 각 부품에 대한 예측 확률을 얻고, 이 예측 확률을 기반으로 이상 구간에서 교체가 필요한 부품을 분류하였다.
3.4 증강방법을 통한 데이터 불균형 해결
고장 부품을 분류할 때, 확실한 이상으로 판정된 구간에서 생성된 잔차 행렬들을 입력으로 사용한다. 하지만 각 이상 구간 길이가 동일하지 않기 때문에 이상 구간에서 발생되는 잔차 행렬 개수도 불균형하게 생성된다. 이러한 불균형 데이터는 고장 부품 분류 성능을 저하시키는 원인이 되며 이를 해결하기 위해 데이터 증강 방법을 적용한다. 데이터 증강은 소수 클래스 샘플을 증가시켜 모델이 더욱 균형 있게 학습하도록 하는 방법이다. 이러한 방법은 불균형 데이터를 해결하는 효과적인 방법 중 하나이며, 모델 정확성을 향상시키는 중요한 전략이다. 본 연구에서는 회전(rotation), 이동(shift), 전단(shear), 자르기(crop), SMOTE, ADASYN, CGAN 그리고BAGAN-GP 총 8가지 데이터 증강 방법을 적용한다(Chawla et al., 2002; He et al., 2008; Huang et al., 2023; Mirza et al., 2014; Shorten et al., 2019).
회전은 원본 데이터를 회전시켜 새로운 관점에서 데이터를 생성하는 방법이다. 이를 통해 모델이 다양한 각도에서 객체나 패턴을 학습할 수 있도록 하는 방법이며 이동은 데이터를 수평 및 수직 방향으로 이동시켜 새로운 위치에서 데이터를 생성하는 방법이다. 전단은 데이터를 기울여서 비선형적인 변화를 주어 다양성을 증가시키는 방법이며, 자르기는 데이터 일부를 잘라내어 새로운 데이터를 생성하는 방법이다. 본 연구에서 회전과 전단은 -45° ~ 45° 범위 사이에서 무작위로 데이터를 생성하였고, 이동은 상, 하, 좌, 우로 -20% ~ 20%를 무작위로 이동한 데이터가 생성되도록 하였다. 자르기는 사이즈를 3으로 설정하여 잔차 행렬을 다양한 위치에서 무작위로 잘라내어 데이터가 생성되도록 하였다.
SMOTE는 소수 클래스 데이터를 증강하는 기술로, 기존 소수 클래스 데이터 사이에서 가상 데이터를 생성하여 클래스 불균형을 줄이는 방법을 말하며, ADASYN은 SMOTE와 유사한 방법이지만 소수 클래스 데이터 중 모델이 학습하기 어려운 데이터 방향으로 많은 가중치를 부여하고 해당 데이터 주변에서 더 많은 가상 데이터를 생성함으로써 클래스 불균형을 완화하는 방법이다. 본 연구에서는 SMOTE와 ADASYN을 활용할 때 시드(seed)를 무작위로 변경하면서 데이터를 생성하였다.
CGAN과 BAGAN-GP는 변형된 GAN(generative adversarial network Goodfellow et al., 2014) 모델이며, 해당 모델 구조는 <Figure 6>과 같다.
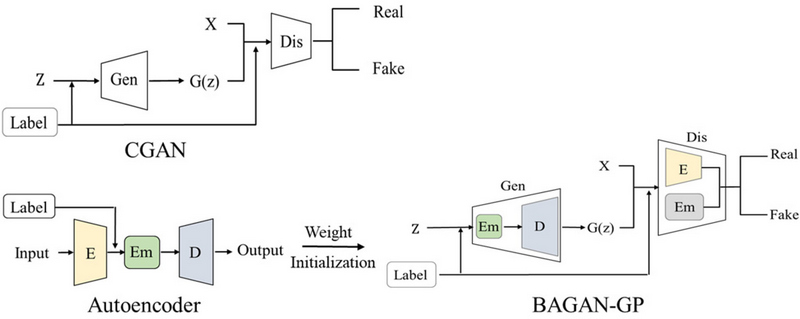
The Structure of CGAN and BAGAN-GP. The Z, X, Em, Gen, Dis, E, D Denote Random Noise, Original Data, Embedding Layer, Generator, Discriminator, Encoder and Decoder, Respectively.
GAN은 생성자(generator)가 무작위 잠재 공간에서 데이터를 생성하면, 판별자(discriminator)는 생성된 데이터와 실제 데이터를 구별하려고 시도하면서 학습 데이터 분포를 모델링하고 새로운 데이터를 생성하는 딥러닝 모델이다. 하지만 GAN은 특정 클래스 데이터만을 따로 생성하도록 직접 조절하는 것은 어렵다. 반면에CGAN과 BAGAN-GP는 클래스 정보를 조건으로 받아서 조건 정보와 데이터를 조합하여 원하는 클래스 또는 소수 클래스 데이터만을 생성하는 것이 가능하다. 이러한 이유로 본 연구에서는 CGAN과BAGAN-GP를 선정하여 사용하였다. CGAN과 BAGAN-GP 둘 다 클래스 정보를 추가적으로 사용한다는 공통점이 있지만 BAGAN-GP는 불균형 데이터가 입력으로 사용될 때 특화된 GAN 모델로, 주로 소수 클래스 데이터 증강을 목적으로 한 모델이라는 차이점이 있다. BAGAN-GP가 불균형 데이터 입력에 특화된 이유는 <Figure 6> 구조에서 확인 할 수 있듯이 데이터 세트를 사용하여 오토인코더를 미리 학습하고 오토인코더 가중치를 BAGAN-GP 내 생성자와 판별자를 초기화하는 데 활용하기 때문이다. 이로써, 생성자와 판별자는 데이터 분포 근사치로부터 학습을 시작하여 안정적인 학습이 가능하고, 생성자와 판별자 내 존재하는 임베딩(embedding) 구조를 GAN 훈련 중에 추가적으로 학습하여 조건 정보를 보다 효과적으로 활용하는 GAN 모델이다. <Appendix> 내 <Table A1>은 CGAN과 BAGAN-GP 구조를 나타내며, 본 연구에서는 100 에폭(epoch) 동안 Adam(Kingma et al., 2014) 최적화 알고리즘과 미니 배치 경사 하강법을 사용하여 모델을 학습하고 소수 클래스 데이터를 생성하였다.
3.5 합성곱 신경망 기반 분류 모델 해석
최근 분류 및 예측 작업에서 딥러닝 알고리즘이 우수한 성능을 보이고 있지만 모델 결과를 이해하고 해석하는 것은 어려운 과제이며 동시에 중요한 과제이다. 딥러닝 모델을 사용할 때, 결과가 어떻게 생성되었는지 이해하고 모델 결정 과정을 설명하는 것은 신뢰성을 향상시키고 사용자에게 필요한 정보를 제공하는 핵심적인 역할을 한다(Arrieta et al., 2020).
본 연구에서는 합성곱 신경망을 해석하여 고장 부품을 예측할 때 고려되는 주요 변수를 확인하기 위해 Grad-CAM을 적용한다. Grad-CAM은 모델 출력과 관련된 가중치 정보(gradient)를 활용하여 합성곱 신경망이 데이터 내에서 어떤 부분을 주목하고 예측을 수행하였는지 이해하는 데 도움을 주는 기법이다. 이 기법은 주로 시각적으로 설명성을 제공하고 모델 의사결정 과정을 해석하는데 활용된다(Selvaraju et al., 2017). 따라서 Grad-CAM을 합성곱 신경망 마지막 층을 기준으로 적용하여 고장 부품을 예측할 때 잔차 행렬 내 어떤 부분이 기여되는지 시각적으로 확인하고 고장 부품과 관련된 주요 변수를 파악한다.
4. 실험 결과
4.1 데이터 수집 및 전처리
본 연구에서 사용된 데이터는 8인치 실리콘 웨이퍼를 사용하여 반도체를 생산하는 국내 A 반도체 기업 에싱(Ashing) 공정 설비 다변량 시계열 데이터로 총 242,780건 수집되었으며 정상 데이터는 227,913건(94%), 비정상 데이터는 14,867건(6%)으로 구성되었다. 입력 변수는 온도, 설비 내 압력, 가스 종류별 유량, 전력 등 총 7가지가 사용되었고 대상 변수는 두 가지 레이블을 사용하였다. 첫 번째 레이블은 설비 정상 구간과 비정상 구간 상태를 나타내고 두 번째 레이블은 각 비정상 구간에서 교체된 부품을 나타낸다. 비정상 구간은 총 6구간이 존재하며 단기 비정상 구간 2건(0.004%, 0.16%), 중기 비정상 구간 3건(0.84%, 1.29%, 1.39%), 장기 비정상 구간 1건(2.4%)으로 구성되고 각 비정상 구간에는 설비 고장 주요 원인을 나타내는 부품 레이블이 존재한다. 해당 데이터 구조를 <Table 2>에 정리하여 나타내었다.
레이블을 수치화하기 위해, 원-핫 인코딩(one-hot encoding)을 적용하여 상태 레이블에서 정상은 0, 비정상은 1로 변환하였고 부품 레이블은 6개 클래스가 존재하기 때문에, 부품 A는100000, 부품 B는 010000으로 변환했으며 동일한 방식으로 부품 C부터 부품 F까지 001000 ~ 000001로 변환하였다. 이어서, time window는 100으로 설정하고 보폭은 5로 설정하여 time window가 이동하는 동안, time window 내 비정상 레이블(1)이 포함될 경우 해당 데이터 세트 레이블을 비정상(1)으로 지정해 주는 작업을 하였다. 또한, time window 내 데이터 세트가 비정상(1)으로 지정될 경우, 원-핫 인코딩으로 변환된 부품 레이블이 두 번째 레이블로 설정되었다. 전처리 된 데이터는 학습 데이터(64%), 검증 데이터(16%) 그리고 평가 데이터(20%)로 분할하여 분석을 진행하였다. 평가 데이터는 비정상 데이터와 정상 데이터로 구성되었으며, 학습 및 검증데이터는 정상 데이터로만 구성되었다. 학습 데이터 정규화를 위해 평균과 표준편차를 각각 0과 1로 하는 z-score 방법을 사용하였고, 학습 데이터 평균과 분산을 사용하여 검증 및 평가 데이터를 정규화하였다.
4.2 평가 지표
본 연구에서는 이상 탐지 알고리즘 성능을 평가하기 위해 정밀도(precision), 재현율(recall), F1 점수(F1 score)를 사용하였다. 또한 분류 알고리즘 성능을 평가하기 위해 정확도(accuracy)를 사용하였다. 정밀도는 실제 정상 데이터 대비 모델이 정상으로 정확하게 예측한 데이터 비율이며, 재현율은 실제 비정상 데이터 대비 모델이 비정상으로 정확하게 예측한 데이터 비율을 의미한다. F1 점수는 정확도와 재현율 조화 평균을 의미하며 정확도는 모델이 올바르게 예측한 데이터 비율을 의미한다. 구체적인 수식은 식 (4)~식 (7)과 같다.
| (4) |
| (5) |
| (6) |
| (7) |
TP(true positive)는 실제 불량을 불량으로 올바르게 예측한 경우, FP(false positive)는 실제 정상을 불량으로 잘못 예측한 경우, FN(false negative)은 실제 불량을 정상으로 잘못 예측한 경우, TN(true negative)은 실제 정상을 정상으로 올바르게 예측한 경우를 의미한다.
4.3 이상탐지 성능
본 연구에서는 특징 행렬을 적용했을 때 이상 탐지 결과에 미치는 영향을 확인하기 위해 다변량 시계열 데이터를 특징 행렬로 변환하기 전후 이상 탐지 성능을 비교하였다. 즉, <Figure 1>에서 다변량 시계열 데이터 내 time window 설정 후 특징 행렬 변환을 생략하고 time window 내 원시 데이터를 입력으로 사용한 경우와 특징 행렬로 변환하여 입력으로 사용한 경우를 비교하였다. 합성곱 오토인코더는 최적화 알고리즘으로 Adam을 사용하였으며, 미니 배치 경사 하강법을 통해 30 에폭 동안 학습하였다. 실험은 5회 반복되었으며, 평균 및 표준편차 값은 <Table 3>과 같다.
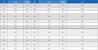
Performance Comparison of Anomaly Detection in Terms of Average Values of Precision, Recall, and F1 Scores. Standard Deviations are Shown in Parentheses.
특징 행렬을 적용하였을 때 정밀도, 재현율 그리고 F1 점수 모두에서 사용하지 않았을 때 대비 성능이 향상되는 것을 확인 할 수 있었다. 이는 특징 행렬이 변수들 간 관계성을더 정밀하게 반영하여 정상 과 비정상 패턴을 더욱 정확하게 식별할 수 있게 되었기 때문에 이상 탐지 성능이 향상되었음을 의미한다.
4.4 고장 부품 분류 성능
이상 탐지 후 비정상 구간에서 교체가 필요한 부품을 예측하기 위해 부품 분류를 실시하였다. 확실한 비정상으로 판정된 구간에서 생성된 잔차 행렬들을 입력(X)으로, 부품 레이블을 출력(Y)으로 설정하여 지도 학습 방식으로 합성곱 신경망 모델을 학습하였다. 모델은 50 에폭 동안 Adam 최적화 알고리즘과 미니 배치 경사 하강법을 활용하여 학습하였으며, 실험은 10회 반복 진행하여 각 부품별 분류 정확도 결과를 확인하였고 결과는 <Table 4>와 같다.

Classification Performance Reported Using the Averaged Accuracy Score and Standard Deviation (in parentheses)
부품별 분류 정확도를 확인한 결과, 부품 A와 부품 E 분류 정확도가 각각 0과 0.612로 낮은 분류 성능을 보여주었다. 이에 대한 원인을 분석한 결과, 이상 구간 불균형이 잔차 행렬 개수 불균형으로 이어져 합성곱 신경망이 제대로 학습되지 못한 것으로 판단되었다. <Table 5>는 부품 클래스별 잔차 행렬 개수를 나타낸다.
이러한 결과를 통해 불균형한 데이터가 분류 모델 성능에 부정적인 영향을 미치고 있음을 확인할 수 있었고 이에 따라 이상으로 판정된 구간에서 생성되는 잔차 행렬 개수 불균형을 개선하는 방안이 필요하다고 판단되었다.
4.5 데이터 증강 기반 고장 부품 분류 성능
부품 클래스별 잔차 행렬개수 불균형 문제를 해결하기 위해 데이터 증강 기법을 적용하였다. 학습 데이터 중 낮은 분류 성능을 보였던 부품 A와 부품 E 잔차 행렬 개수를 증강하였으며, 부품 F 개수를 참조하여 최대 588개로 증강하였고, <Table 6>은 데이터 증강 전후 학습 데이터 개수를 나타낸다.
총 8가지 방법(회전, 이동, 전단, 자르기, SMOTE, ADASYN, CGAN 그리고 BAGAN-GP)을 각각 적용하여 학습 데이터를 증강하였다. 각각 증강된 학습 데이터를 입력으로 사용하여 지도 학습 방식으로 합성곱 신경망 모델을 50 에폭 동안 학습하였으며, 최적화 알고리즘으로는 Adam을 사용하고 미니 배치 경사 하강법을 적용하였다. 실험은 10회 반복 진행하였으며, 부품별 분류 모델 결과는 <Table 7>과 같다.

Comparison of Classification Performance after Applying Data Augmentation Methods in Terms of Average Value of Accuracy. Standard Deviations are Shown in Parentheses
데이터 증강 방법 8가지를 적용한 결과, 부품 A와 부품 E 분류 정확도 성능이 크게 향상되는 것을 확인하였다. 특히, 일반적인 증강 방법들(회전, 전단, 이동 그리고 자르기)보다 머신러닝과 딥러닝 방법(SMOTE, ADASYN, CGAN 그리고 BAGAN-GP)에서 더 높은 성능 향상을 확인 할 수 있었으며, 그중에서 BAGAN-GP를 사용하여 증강하였을 때 가장 높은 성능 향상을 보였다.
4.6 Grad-CAM을 통한 주요 변수 분석
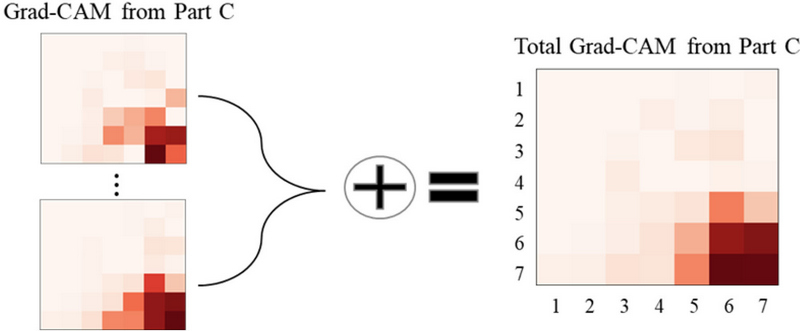
BAGAN-GP를 사용하여 증강하였을 때 가장 높은 정확도 성능을 보였기 때문에, 해당 합성곱 신경망을 Grad-CAM으로 해석하였으며 부품 클래스를 올바르게 예측한 경우만 Grad-CAM을 적용하였다. 이후, 부품 예측과 관련된 중요한 영역과 특징을 명확하게 식별하고 시각화하기 위해 Grad-CAM 결과들을 통합하여 Total Grad-CAM을 생성하였다. <Figure 7>은 Total Grad-CAM을 생성하는 예시로, 부품 C 경우를 보여준다.
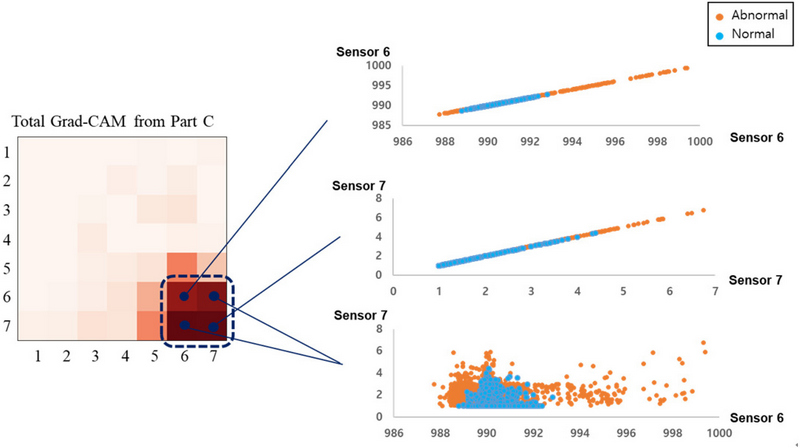
Total Grad-CAM에서 보여지는 어두운 영역은 부품 예측을 할 때 가장 큰 영향을 미치는 부분으로 해석할 수 있으며, 이를 통해 모델이 부품을 예측하는 데 중요한 역할을 하는 주요 변수 영역을 시각적으로 확인 할 수 있었다. 또한, 해당 영역을 분석하여 주요 변수 분석을 수행한 예시를 <Figure 8>을 통해 나타내었다. 해당 예시에서 6번 센서와 7번 센서 간 상관관계나 패턴에서 문제가 있음을 고려해 볼 수 있다. 우선, 6번 센서와 7번 센서 각각 정상 데이터와 비정상 데이터 산점도(scatter plot)를 살펴본 결과, 두 센서 모두 비정상 분포가 정상 분포와 큰 차이를 보임을 확인할 수 있었다. 추가적으로, 6번 센서와 7번 센서 간 산점도를 확인해 보았을 때, 비정상 데이터 분포가 정상과는 다른 패턴을 보이는 것을 확인할 수 있었고, 6번 센서 데이터가 증가할 때 7번 센서 데이터도 증가하는 관계를 확인할 수 있었다. 이러한 결과를 토대로 6번 센서와 7번 센서가 부품 C와 관련이 있다는 것으로 해석할 수 있고, 이는 Grad-CAM 결과와 함께 고려할 때, 이 두 센서의 데이터 패턴이 부품 C 예측에 중요한 정보로 사용되었다는 것을 뜻한다.
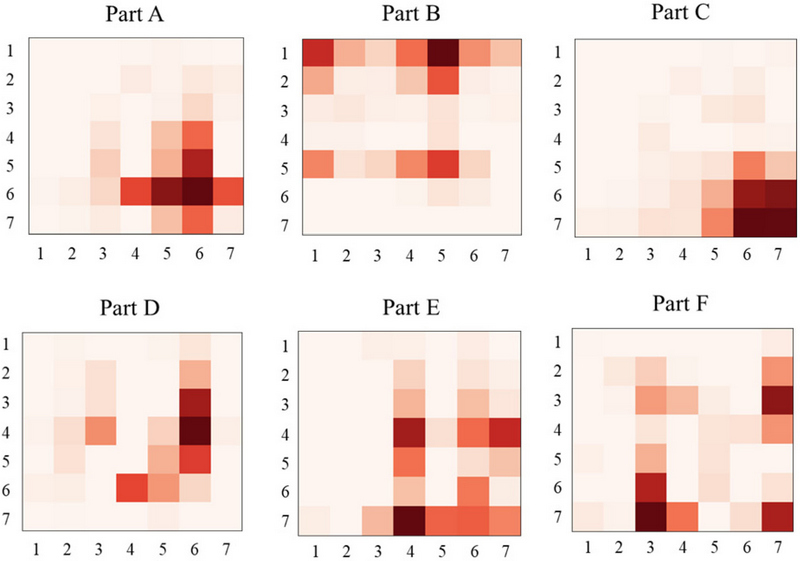
동일한 방법을 적용하여 부품 A부터 부품 F까지 클래스별 Total Grad-CAM을 생성하였고 이를 <Figure 9>로 나타내었다. 특히, 부품 D의 경우와 같이 Total Grad-CAM 결과가 대칭 행렬이 아닌 형태로 나타날 수 있는데, 이는 합성곱 신경망이 데이터의 특정 부분에 더 많은 주의를 기울이는 학습 특성 때문이다. 이러한 특성은 잔차 행렬의 특정 부분이 다른 부분보다 더 중요하게 학습되는 결과를 초래할 수 있으며, Grad-CAM 결과가 대칭 행렬이 아닌 결과로 나타날 수 있다. 하지만 이러한 경우가 모델의 해석이나 예측 정확성에 문제가 있다는 것을 의미하지는 않는다. Grad-CAM에서 가장 어두운 부분은 모델이 해당 클래스를 예측할 때 가장 중요하게 고려한 영역을 나타내므로 해당 부분이 비정상적인 패턴이나 이상치를 나타낼 수 있음을 의미하며, 모델이 이러한 정보를 중요하게 여기고 있다는 것을 보여준다. 따라서, 부품D의 경우와 같이 Grad-CAM 결과가 대칭 행렬이 아닌 결과가 나타날 수 있지만, 현재 결과에서 어두운 영역을 통해 부품을 예측하는 데 관여한 주요 변수를 확인할 수 있다. 이를 통해, 각 고장 부품과 관련된 센서 간 상관관계 및 패턴 이상 정보를 확인할 수 있고 이러한 정보는 설비 엔지니어에게 설비 유지보수 및 구조 개선 작업과 관련하여 도움을 줄 수 있으며, 공정 엔지니어에게 공정 제어 및 신제품 개발을 효율화하는 데 기여할 수 있을 것으로 예상된다.
5. 결 론
최근 반도체 시장 수요가 꾸준히 증가하고 있으며, 반도체 미세화가 진행되면서 생산성과 품질 유지가 점점 어려워지고 있다. 이에 따라 공정 설비 상태를 정확하게 진단하고 분석하는 것이 매우 중요해졌다. 이러한 요구에 맞춰 본 연구는 반도체 제조 공정에서 설비 이상을 탐지하고 원인을 파악하는 방법을 제시하였다. 다변량 센서 데이터 변수 간 상관관계를 반영하기 위해 특징 행렬을 생성하고, 이를 이상 탐지를 위한 합성곱 오토인코더 모델 입력으로 활용하였다. 또한, 확실한 이상 구간에서 생성된 잔차 행렬을 합성곱 신경망 입력으로 사용하여 교체해야 할 부품을 예측하였다. 이때, 부품 클래스별 잔차 행렬 개수 불균형을 해결하기 위해 데이터 증강 기법을 도입하였다. 더불어, Grad-CAM을 활용하여 고장 부품을 예측하는 데 큰 기여를 한 주요 요인을 식별하였으며, 이 정보는 엔지니어 업무에서 유용하게 활용될 것으로 기대된다. 하지만 본 연구에서는 모든 이상 구간에서 레이블이 있는 데이터를 활용하였지만 실제 현장에서 레이블 작업을 하는 것은 많은 비용이 들며, 어려움을 겪게 된다. 따라서, 향후에는 레이블 작업 비용과 어려움을 극복하면서도 효과적으로 모델을 학습할 수 있는 자기 지도 학습(self-supervised learning) 또는 준 지도 학습 방법(semi-supervised learning)을 탐구하고 적용하는 연구를 진행할 예정이다.
References
-
Arrieta, A. B., Díaz-Rodríguez, N., Del Ser, J., Bennetot, A., Tabik, S., Barbado, A., ... and Herrera, F. (2020), Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI, Information fusion, 58, 82-115.
[https://doi.org/10.1016/j.inffus.2019.12.012]

-
Awais, M. and Haq, A. (2018), A new cumulative sum control chart for monitoring the process mean using varied L ranked set sampling, Journal of Industrial and Production Engineering, 35(2), 74-90.
[https://doi.org/10.1080/21681015.2017.1417787]

-
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer, W. P. (2002). SMOTE: synthetic minority over-sampling technique, Journal of Artificial Intelligence Research, 16, 321-357.
[https://doi.org/10.1613/jair.953]

-
Chen, Z., Yeo, C. K., Lee, B. S., and Lau, C. T. (2018, April). Autoencoder-based network anomaly detection, In 2018 Wireless telecommunications symposium (WTS), IEEE, 1-5.
[https://doi.org/10.1109/WTS.2018.8363930]

-
Chien, C. F. and Hsu, C. Y. (2011), UNISON analysis to model and reduce step-and-scan overlay errors for semiconductor manufacturing, Journal of Intelligent Manufacturing, 22, 399-412.
[https://doi.org/10.1007/s10845-009-0298-2]

-
Chien, C. F., Hsu, C. Y., and Chen, P. N. (2013), Semiconductor fault detection and classification for yield enhancement and manufacturing intelligence, Flexible Services and Manufacturing Journal, 25, 367-388.
[https://doi.org/10.1007/s10696-012-9161-4]

-
Cho, M. Y. and Baek, J. G. (2012), One-Class Classification Based Fault Classification for Semiconductor Process Cyclic Signal, IE Interfaces, 25(2), 170-177.
[https://doi.org/10.7232/IEIF.2012.25.2.170]

-
David, O. E. and Netanyahu, N. S. (2016), Deeppainter: Painter classification using deep convolutional autoencoders, In Artificial Neural Networks and Machine Learning–ICANN 2016: 25th International Conference on Artificial Neural Networks, Barcelona, Spain, September 6-9, 2016, Proceedings, Part II 25 (pp. 20-28), Springer International Publishing.
[https://doi.org/10.1007/978-3-319-44781-0_3]

-
Fan, S. K. S., Hsu, C. Y., Jen, C. H., Chen, K. L., and Juan, L. T. (2020), Defective wafer detection using a denoising autoencoder for semiconductor manufacturing processes, Advanced Engineering Informatics, 46, 101166.
[https://doi.org/10.1016/j.aei.2020.101166]

- Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... and Bengio, Y. (2014), Generative adversarial nets, Advances in Neural Information Processing Systems, 27.
- He, H., Bai, Y., Garcia, E. A., and Li, S. (2008, June), ADASYN: Adaptive synthetic sampling approach for imbalanced learning, In 2008 IEEE international joint conference on neural networks (IEEE world congress on computational intelligence), IEEE, 1322-1328.
-
He, Q. P. and Wang, J. (2007), Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes, IEEE Transactions on Semiconductor Manufacturing, 20(4), 345-354.
[https://doi.org/10.1109/TSM.2007.907607]

-
Hosseinpour, F., Ahmed, I., Baraldi, P., Behzad, M., Zio, E., and Lewitschnig, H. (2022), An unsupervised method for anomaly detection in multiystage production systemsbased on LSTM autoencoders, In Proc. 32nd Eur. Saf. Rel. Conf.(ESREL), Singapore: ESREL.
[https://doi.org/10.3850/978-981-18-5183-4_R22-19-604]

-
Huang, G. and Jafari, A. H. (2023), Enhanced balancing GAN: Minority-class image generation, Neural Computing and Applications, 35(7), 5145-5154.
[https://doi.org/10.1007/s00521-021-06163-8]

-
Jahan, I., Alam, M. M., Ahmed, M. F., and Jang, Y. M. (2021, October), Anomaly Detection in Semiconductor Cleanroom Using Isolation Forest. In 2021 International Conference on Information and Communication Technology Convergence (ICTC), IEEE, 795-797.
[https://doi.org/10.1109/ICTC52510.2021.9621047]

-
Jang, J., Min, B. W., and Kim, C. O. (2019), Denoised residual trace analysis for monitoring semiconductor process faults, IEEE Transactions on Semiconductor Manufacturing, 32(3), 293-301.
[https://doi.org/10.1109/TSM.2019.2916374]

-
Jeong, Y. S., Kim, B., and Ko, Y. D. (2013), Exponentially weighted moving average-based procedure with adaptive thresholding for monitoring nonlinear profiles: Monitoring of plasma etch process in semiconductor manufacturing, Expert Systems with Applications, 40(14), 5688-5693.
[https://doi.org/10.1016/j.eswa.2013.04.016]

- Kim, C. G. and Kang, J. W.(2017), Anomaly Detection in Semiconductor Manufacturing Data Using LSTM, Proceedings of the Korean Institute of Information Scientists and Engineers, 760-762.
- Kingma, D. P. and Ba, J. (2014), Adam: A method for stochastic optimization, arXiv preprint arXiv:1412.6980, .
- Klambauer, G., Unterthiner, T., Mayr, A., and Hochreiter, S. (2017), Self-normalizing neural networks, Advances in Neural Information Processing Systems, 30.
-
Kourti, T. and MacGregor, J. F. (1995), Process analysis, monitoring and diagnosis, using multivariate projection methods, Chemometrics and Intelligent Laboratory Systems, 28(1), 3-21.
[https://doi.org/10.1016/0169-7439(95)80036-9]

- Kuchaiev, O. and Ginsburg, B. (2017), Training deep autoencoders for collaborative filtering, arXiv preprint arXiv:1708.01715, .
-
Lee, H., Kim, Y., and Kim, C. O. (2016), A deep learning model for robust wafer fault monitoring with sensor measurement noise, IEEE Transactions on Semiconductor Manufacturing, 30(1), 23-31.
[https://doi.org/10.1109/TSM.2016.2628865]

-
Liao, D. Y., Chen, C. Y., Tsai, W. P., Chen, H. T., Wu, Y. T., and Chang, S. C. (2018, December), Anomaly detection for semiconductor tools using stacked autoencoder learning, In 2018 International Symposium on Semiconductor Manufacturing (ISSM), IEEE, 1-4.
[https://doi.org/10.1109/ISSM.2018.8651179]

-
Liu, B., Noor-ul-Amin, M., Khan, I., Ismail, E. A., and Awwad, F. A. (2023), Integration of Bayesian adaptive exponentially weighted moving average control chart and paired ranked-based sampling for enhanced semiconductor manufacturing process monitoring, Processes, 11(10), 2893.
[https://doi.org/10.3390/pr11102893]

-
Michau, G., Hu, Y., Palmé, T., and Fink, O. (2020), Feature learning for fault detection in high-dimensional condition monitoring signals, Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 234(1), 104-115.
[https://doi.org/10.1177/1748006X19868335]

- Mirza, M. and Osindero, S. (2014), Conditional generative adversarial nets, arXiv preprint arXiv:1411.1784, .
-
Pang, G., Shen, C., Cao, L., and Hengel, A. V. D. (2021), Deep learning for anomaly detection: A review, ACM computing surveys (CSUR), 54(2), 1-38.
[https://doi.org/10.1145/3439950]

- Park, S. H., Kim, J. S., Park, C. S., Kim, S. S., and Baek, J. G. (2010), A fault detection of cyclic signals using support vector machine-regression, Journal of Korean Society for Quality Management, 38(3), 354.
-
Raji, I. A., Lee, M. H., Riaz, M., Abujiya, M. A. R., andAbbas, N. (2020), Outliers detection models in shewhart control charts; An application in photolithography: A semiconductor manufacturing industry, Mathematics, 8(5), 857.
[https://doi.org/10.3390/math8050857]

-
Ruff, L., Kauffmann, J. R., Vandermeulen, R. A., Montavon, G., Samek, W., Kloft, M., ... and Müller, K. R. (2021), A unifying review of deep and shallow anomaly detection, Proceedings of the IEEE, 109(5), 756-795.
[https://doi.org/10.1109/JPROC.2021.3052449]

-
Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., and Batra, D. (2017), Grad-cam: Visual explanations from deep networks via gradient-based localization, In Proceedings of the IEEE International Conference on Computer Vision, 618-626.
[https://doi.org/10.1109/ICCV.2017.74]

-
Shorten, C. and Khoshgoftaar, T. M. (2019), A survey on image data augmentation for deep learning, Journal of Big Data, 6(1), 1-48.
[https://doi.org/10.1186/s40537-019-0197-0]

-
Susto, G. A., Terzi, M., and Beghi, A. (2017). Anomaly detection approaches for semiconductor manufacturing, Procedia Manufacturing, 11, 2018-2024.
[https://doi.org/10.1016/j.promfg.2017.07.353]

-
Tchatchoua, P., Graton, G., Ouladsine, M., Muller, J., Traoré, A., and Juge, M. (2022, July), 1D ResNet for fault detection and classification on sensor data in semiconductor manufacturing. In 2022 International Conference on Control, Automation and Diagnosis (ICCAD), IEEE, 1-6.
[https://doi.org/10.1109/ICCAD55197.2022.9853997]

-
Thieullen, A., Ouladsine, M., and Pinaton, J. (2013, May), Application of PCA for efficient multivariate FDC of semiconductor manufacturing equipment, In ASMC 2013 SEMI Advanced Semiconductor Manufacturing Conference, IEEE, 332-337.
[https://doi.org/10.1109/ASMC.2013.6552755]

-
Thieullen, A., Ouladsine, M., and Pinaton, J. (2013, July), Application of Principal Components Analysis to improve fault detection and diagnosis on semiconductor manufacturing equipment, In 2013 European Control Conference (ECC), IEEE, 1445-1500.
[https://doi.org/10.23919/ECC.2013.6669553]

- Tomar, V. S. (2022), A critical evaluation of activation functions for autoencoder neural networks (Doctoral dissertation, Dublin, National College of Ireland).
-
Yong, W., Xu, C., and Zhengying, W. (2020, June), Fault detection of sensor data in semiconductor processing with variationalautoencoder neural network, In 2020 China Semiconductor Technology International Conference (CSTIC), IEEE, 1-3.
[https://doi.org/10.1109/CSTIC49141.2020.9282417]

-
Yoon, J. S. and Kwak, K. H.(2021), Research and Development Strategies Considering the Ripple Effects of Intelligent Information Technology: Focusing on the Bio, Automotive, and Semiconductor Industries, Journal of the Korean Society for Innovation, 16(1), 95-119.
[https://doi.org/10.46251/INNOS.2021.2.16.1.95]

-
Zhang, C., Song, D., Chen, Y., Feng, X., Lumezanu, C., Cheng, W., ... and Chawla, N. V. (2019, July), A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data, In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 33, No. 01, pp. 1409-1416).
[https://doi.org/10.1609/aaai.v33i01.33011409]

-
Zhang, H., Wang, P., Gao, X., Gao, H., and Qi, Y. (2020, February), Automated Fault Detection Using Convolutional Auto Encoder and k Nearest Neighbor Rule for Semiconductor Manufacturing Processes, In 2020 3rd International Conference on Intelligent Autonomous Systems (ICoIAS), IEEE, 83-87.
[https://doi.org/10.1109/ICoIAS49312.2020.9081852]

Appendix
<Appendix>
<Table A1>은 CGAN과 BAGAN-GP의 상세한 구조를 나타낸다. 이들의 주요 차이점은 클래스 정보를 조건으로 사용하는 방식에 있다. CGAN은 클래스 정보를 원-핫 인코딩 형태로 변환하여 입력으로 사용하며, 이를 통해 특정 클래스 데이터 생성을 조절한다. 반면, BAGAN-GP는 임베딩 구조를 사용하여 클래스 정보를 더 효과적으로 통합할 수 있다. 이러한 접근은 전통적인 GAN과 비교했을 때, 보다 정밀한 클래스 조건부 데이터 생성을 가능하게 한다.
백민재: 경북대학교 전자공학부에서 2016년 학사 학위를 취득하고, 고려대학교 산업경영공학과에서 석사과정에 재학 중이다. 연구 분야는 머신러닝, 딥러닝을 적용한 이상 탐지와 산업 분야에 응용하는 연구를 수행하고 있다.
김성범: 고려대학교 산업경영공학부 교수로 2009년부터 재직하고 있으며, 인공지능공학연구소 소장, 기업산학연협력센터 센터장, 한국데이터마이닝학회 회장을 역임했다. 미국 University of Texas at Arlington 산업공학과에서 교수를 역임하였으며, 한양대학교 산업공학과에서 학사학위를 미국 Georgia Institute of Technology에서 산업시스템공학 석사 및 박사학위를 취득하였다. 인공지능, 머신러닝, 최적화 방법론을 개발하고 이를 다양한 공학, 자연과학, 사회과학 분야에 응용하는 연구를 수행하고 있다.