공정개선을 위한 중앙점 추가 요인배치법과 한번에 한인자 실험의 비교

1. 서 론

실험계획법을 쓰지 않는 실험자는 실험에서 고려하는 여러 인자 중 한 인자의 수준 값만 변경하여 더 나은 실험 결과를 보이는 수준을 선택하고, 다른 인자들에 대해서도 같은 방법으로 실험을 진행한다. 이런 방법을 ‘한번에 한인자(One-Factor-At-a-Time; OFAT) 실험’이라고 부른다. OFAT 실험 대신 실험계획의 대표적 방법인 2수준 요인배치법을 사용하는 것이 여러 측면에서 우수하지만(Wu and Hamada, 2009), 인자의 곡률효과를 추정할 수 없다는 단점이 있다. 이를 보완하기 위해 중앙점에서 추가로 실험하여 데이터를 분석하면 곡률효과의 존재 여부를 파악할 수 있고, 곡률효과가 있다고 판정되면 축점을 추가하여 어떤 인자가 이러한 효과를 일으키는지 알 수 있다(Wu and Hamada, 2009; Myers et al., 2016). 하지만 여전히 실험자들은 실험계획을 배우지 못했거나 배웠더라도 기존 습관에 이끌려 요인배치법을 쓰지 않는 경우가 흔하다(Knowlton and Keppinger, 1993).

현업에서 가동 중인 공정을 개선할 때도 대부분 현재 운영조건을 가운데에 놓고 변수별로 이 조건보다 작은 쪽과 큰 쪽으로 2개의 수준을 정하여 실험하는 OFAT 실험방법을 사용해 왔다. OFAT 실험 대신 현재 조건을 중앙점에 배치하고, 이를 중심으로 인자의 수준 값을 낮추고 높여 실험점을 둘러서 배치한다면 중앙점이 있는 2수준 요인배치법의 형태로 나타낼 수 있다. 실험데이터를 분석하여 곡률효과가 있다고 판단되었을 때, 요인배치 실험점에 축점을 추가하여 실험하면 어떤 인자가 곡률효과를 가졌는지 알 수 있다. 본 논문에서는 중앙점을 추가한 2수준 요인배치 실험방법이 OFAT 실험에 비하여 실험 횟수, 실험영역, 모형식, 설계최적화기준 측면에서 우수함을 보이고자 한다.

본 논문의 구성은 다음과 같다. 제2장에서는 중앙점을 추가한 2수준 요인배치 실험의 기본 내용을 설명한다. 제3장에서는 이를 현행 공정개선에 활용하는 방법을 제안하고, 이 방법과 OFAT 실험방법을 비교한 결과를 기술한다. 사례 데이터를 이용하여 두 가지 방법으로 얻은 데이터를 분석하여 비교한 결과를 제4장에 제시하고, 제5장에서 본 연구의 내용을 요약한다.

2. 중앙점 추가 2수준 요인배치 실험

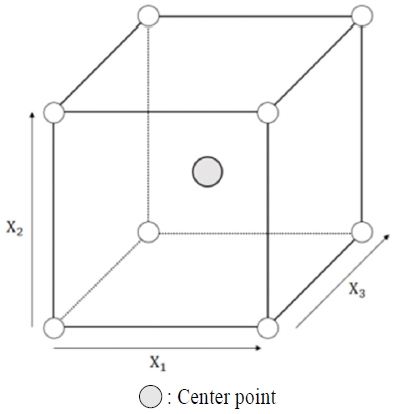
2수준 요인배치법에서 중앙점(center point)은 인자별로 낮은 수준과 높은 수준의 한가운데 위치한 수준들로 이루어진 실험조건을 말한다. 코딩된 수준 값을 기준으로 말하면, 인자별로 코딩한 수준 값인 –1수준, +1수준의 중간에 있는 0수준으로 이루어진 실험점이다(<Figure 1>).

Figure 1.

23 Factorial Design with Center Point

2^k 요인배치 실험을 하면, 1차 효과, 2인자 교호작용효과 등을 알 수 있지만, 인자별 2차 효과는 알 수 없다. 2차 효과를 알기 위해서는 3수준 실험을 시행해야 한다. 하지만 수준 수를 2개에서 3개로 늘리면 실험점의 수가 2^k에서 3^k로 늘어난다. k=4일 경우, 실험점의 수가 16개에서 81개로 65개 증가한다. 이렇게 실험점 수가 급격하게 늘어나지 않도록 하면서 곡률효과(curvature effect)를 파악하는 방법은 2^k 요인배치 중앙점에서 n_c개의 반복실험을 추가하는 것이다. 이 방법으로 실험하여 얻은 데이터를 분석하면 실험영역 내에서 곡률효과의 존재 여부를 알 수 있고, 중앙점의 반복 실험데이터를 이용하여 실험오차를 추정할 수 있다. 실험데이터를 분석하여 곡률효과가 있다는 판정이 나면, 곡률효과를 일으킨 인자를 알기 위하여 각 인자의 가운데 수준에서 양쪽으로 일정한 거리에 있는 축점을 이용하여 총 2k개 실험을 추가로 시행하게 된다. 이렇게 곡률효과가 있을 때 요인배치 실험점에 축점을 추가하여 결합하면 중심합성계획(Central Composite Design; CCD)이 된다.

3. 현행 공정개선을 위한 한번에 한인자 실험과 중앙점 추가 요인배치 실험

인자 수준 값을 변경하여 프로세스를 개선할 때 현행 조건을 중앙점으로 삼아 ‘중앙점을 추가한 2수준 요인배치 실험방법’을 제안하고 OFAT 실험방법과 비교하고자 한다. 현행 조건에서 이미 충분한 데이터를 보유하고 있으므로 중앙점에서는 별도의 실험을 진행하지 않아도 되고, 만일 요인배치나 OFAT 실험을 시행할 때 실험환경의 변화가 우려되면 중앙점 실험을 추가할 수도 있다.

3.1 설계공간과 실험 수의 비교

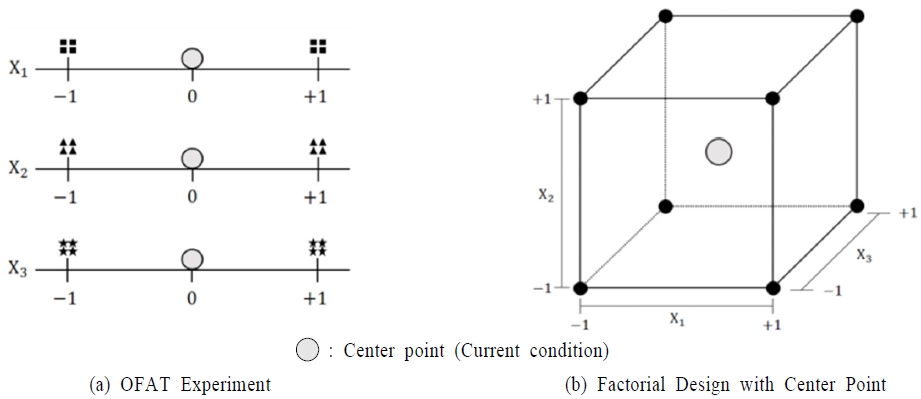
실험 인자가 2개, 3개일 때 설계영역을 각각 <Figure 2>, <Figure 3>에 나타내었다. 여기서 OFAT 실험은 2인자의 경우 2회, 3인자는 4회 반복 실험을 시행하였는데, 이는 2^k 요인배치실험과 효과 추정의 정밀도(precision)를 맞추기 위함이다. 2^k 요인배치실험의 요인효과는 –1, +1 수준에서 각각 2^k-1회 ‘잠재적 반복’ 데이터 평균을 계산하여 그 차이 값으로 구한다. 따라서 요인배치법과 같은 정도의 반복에 의한 수준별 평균값을 구하기 위해서는 OFAT 방법도 각 실험점에서 2^k-1번 반복해야 한다.

Figure 2.

Design Region for Two Factors

Figure 3.

Design Region for Three Factors

중앙점을 제외한 실험 횟수를 비교해보자. k개 인자 2수준 요인배치의 실험횟수는 2^k이다. OFAT 실험을 k개의 인자별로 각 수준에서 2^k-1번 반복 실험을 하면 총 실험횟수가 k×2×2^k-1이므로 2수준 요인배치 실험 횟수 2^k보다 k배 많다. 3인자의 경우, 요인효과를 수준별 4개의 데이터 평균 차이로 구하려면, 요인배치는 2³=8번, OFAT 실험은 3×2×2²=24번 실험해야 한다. 곡률효과가 있다고 판정이 나와, 2차 효과를 추정하기 위해 축점을 추가하더라도 OFAT의 실험 수 k×2×2^k-1는 k≥2일 때 요인배치와 축점의 실험 수를 합한 2^k+2k 보다 크거나 같다.

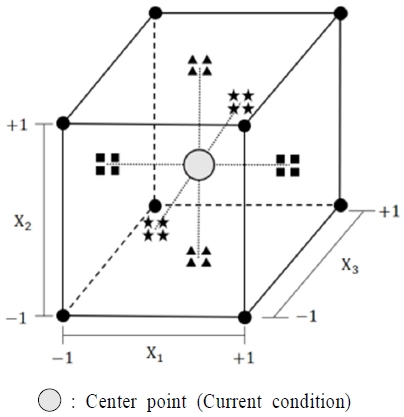
실험영역의 범위를 보면, 요인배치법을 쓰는 것이 OFAT 실험보다 더 넓은 지역을 탐색할 수 있다. <Figure 4>는 3인자 실험에서 두 가지 방법을 썼을 때 탐색하는 실험영역의 범위를 비교한 것이다.

Figure 4.

Coverage of Experimental Regions for Three Factors

3.3 OFAT과 요인배치 설계 비교

두 가지 실험계획 방법을 설계최적화기준(Design Optimality Criteria) 측면에서 비교하기 위하여 회귀계수의 분산-공분산 행렬을 바탕으로 분산을 평가하는 데 자주 쓰이는 D-최적화(D-Optimality)와 A-최적화(A-Optimality)를 적용하였다. D-최적화 기준은 모멘트(Moment) 행렬 M을 사용하여 회귀계수 추정의 정확성을 파악하는 방법이다. 모멘트 행렬 M은 식 (7)에 나타내었는데, X는 모형식을 구하는 데 쓰이는 효과행렬이고, N은 실험 횟수이다.

$\[ M=\frac{{\mathit{X}}^{\text{'}}\mathit{X}}{N} \]$

(7)

회귀계수 추정치의 분산-공분산 행렬은 $$ Cov\left(\widehat{\mathit{\beta }}\right)={\sigma }^2{\left({\mathit{X}}^{\text{'}}\mathit{X}\right)}^{-1}$$이다. 식 (7)의 역행렬을 식 (8)에 나타내었는데, 이는 분산-공분산 행렬에 N/σ²을 곱하여 스케일링한 것과 같다.

$\[ M^{-1}=N{\left({\mathit{X}}^{\text{'}}\mathit{X}\right)}^{-1} \]$

(8)

따라서 스케일링한 분산-공분산 행렬 식 (8)을 최소화하기 위해서는 식 (7)의 모멘트 행렬을 최대화해야 한다. 행렬 자체를 최대화할 수는 없으므로 그것의 행렬식(Determinant)인 |M|을 고려한다(식 (9)). 여기서 p는 절편을 포함한 모형식 항의 개수이다.

$\[ \left|M\right|=\frac{\left|{\mathit{X}}^{\text{'}}\mathit{X}\right|}{N^p} \]$

(9)

오차항이 서로 독립이고 분산이 일정한 정규분포를 따르면, |X' X|는 회귀계수들의 신뢰영역 크기 제곱에 반비례한다. 즉 |X' X|가 클수록 회귀계수들의 신뢰영역은 좁아지므로 좀 더 정확하게 계수들을 추정할 수 있는 것이다. 실제로 두 개 이상의 실험계획을 비교할 때는 식 (9)에 나타낸 행렬식을 p-제곱근 값인 아래 식 (10)의 D^1/p을 이용한다(Myers et al., 2016).

$\[ D^{1/p}={\left(\frac{\left|{\mathit{X}}^{\text{'}}\mathit{X}\right|}{N^p}\right)}^{1/p} \]$

(10)

A-최적화 기준은 회귀계수 추정치 분산의 합을 최소화하는 것이다. i번째 회귀계수 추정치의 분산($$ Var\left({\widehat{\beta }}_i\right)$$)은 행렬 $$ Cov\left(\widehat{\mathit{\beta }}\right)={\sigma }^2{\left({\mathit{X}}^{\text{'}}\mathit{X}\right)}^{-1}$$의 대각원소인 $$ {\sigma }^2{\left({\left({\mathit{X}}^{\text{'}}\mathit{X}\right)}^{-1}\right)}_{ii}$$이다. $$ tr{\left({\mathit{X}}^{\text{'}}\mathit{X}\right)}^{-1}$$을 최소화하는 A-최적화 설계를 하면, 회귀계수 추정치 분산의 합을 작게 만들 수 있다.

공정개선을 위한 두 가지 실험방법을 비교하기 위해 2~5개 인자를 대상으로 효과행렬(Effect Matrix)을 작성하여 설계최적화기준을 계산하였다. 예를 들어, 3인자 대상으로 중심점 3개를 포함한 2수준 요인실험점에서 실험을 시행하고, 곡률효과가 있어서 축점을 추가한 모형의 효과행렬(X_F)과 이로부터 구한 행렬 $$ {\mathit{X}}_F^{\text{'}}{\mathit{X}}_F$$, OFAT 실험의 효과행렬(X_O)과 $$ {\mathit{X}}_O^{\text{'}}{\mathit{X}}_O$$은 각각 다음과 같다:

$\[ {\mathit{X}}_F=\left[\begin{array}{cccccccccc}& X_1& X_2& X_3& X_1{X}_2& X_1{X}_3& X_2{X}_3& X_1^2& X_2^2& X_3^2\\ 1& -1& -1& -1& 1& 1& 1& 1& 1& 1\\ 1& 1& -1& -1& -1& -1& 1& 1& 1& 1\\ 1& -1& 1& -1& -1& 1& -1& 1& 1& 1\\ 1& 1& 1& -1& 1& -1& -1& 1& 1& 1\\ 1& -1& -1& 1& 1& -1& -1& 1& 1& 1\\ 1& 1& -1& 1& -1& 1& -1& 1& 1& 1\\ 1& -1& 1& 1& -1& -1& 1& 1& 1& 1\\ 1& 1& 1& 1& 1& 1& 1& 1& 1& 1\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& -1.682& 0& 0& 0& 0& 0& 2.829& 0& 0\\ 1& 1.682& 0& 0& 0& 0& 0& 2.829& 0& 0\\ 1& 0& -1.682& 0& 0& 0& 0& 0& 2.829& 0\\ 1& 0& 1.682& 0& 0& 0& 0& 0& 2.829& 0\\ 1& 0& 0& -1.682& 0& 0& 0& 0& 0& 2.829\\ 1& 0& 0& 1.682& 0& 0& 0& 0& 0& 2.829\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right] \]$

$\[ {\mathit{X}}_F^{\mathrm{\text{'}}}{\mathit{X}}_F=\left[\begin{array}{cccccccccc}20& 0& 0& 0& 0& 0& 0& 13.66& 13.66& 13.66\\ 0& 13.66& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 13.66& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 13.66& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 8& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 8& 0& 0& 0& 0\\ 20& 0& 0& 0& 0& 0& 8& 0& 0& 0\\ 13.66& 0& 0& 0& 0& 0& 0& 24.01& 8& 8\\ 13.66& 0& 0& 0& 0& 0& 0& 8& 24.01& 8\\ 13.66& 0& 0& 0& 0& 0& 0& 8& 8& 24.01\end{array}\right] \]$

$\[ {\mathit{X}}_O=\left[\begin{array}{ccccccc}& X_1& X_2& X_3& X_1^2& X_2^2& X_3^2\\ 1& -1& 0& 0& 1& 0& 0\\ 1& -1& 0& 0& 1& 0& 0\\ 1& -1& 0& 0& 1& 0& 0\\ 1& -1& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 1& 0& 0\\ 1& 0& -1& 0& 0& 1& 0\\ 1& 0& -1& 0& 0& 1& 0\\ 1& 0& -1& 0& 0& 1& 0\\ 1& 0& -1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 0& 1& 0\\ 1& 0& 0& -1& 0& 0& 1\\ 1& 0& 0& -1& 0& 0& 1\\ 1& 0& 0& -1& 0& 0& 1\\ 1& 0& 0& -1& 0& 0& 1\\ 1& 0& 0& 1& 0& 0& 1\\ 1& 0& 0& 1& 0& 0& 1\\ 1& 0& 0& 1& 0& 0& 1\\ 1& 0& 0& 1& 0& 0& 1\\ 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0\end{array}\right] \]$

$\[ {\mathit{X}}_O^{\mathrm{\text{'}}}{\mathit{X}}_O=\left[\begin{array}{c}30\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\\ 0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 8\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}8\end{array}\right] \]$

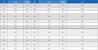
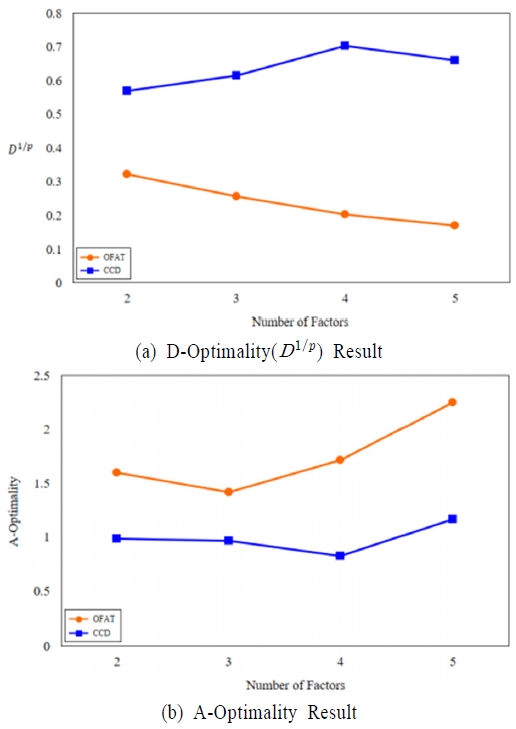
이러한 행렬들을 이용하여 D-최적화 기준인 D^1/p 값과 A-최적화 값을 구한 것을 <Table 1>에 나타내었는데, 중심합성계획이 OFAT 실험방법보다 훨씬 우수하다는 것을 알 수 있다.

Table 1.

Comparison between CCD and OFAT

효과 추정의 정밀도를 요인배치와 맞추려고 OFAT 실험의 각 조건에서 2^k-1회 반복 실험하면, 실험 횟수가 급격하게 증가하므로 4인자 이상일 때는 반복 횟수를 4회로 제한하고 비교하였다. 요인배치법을 이용하여 2인자 교호작용효과까지 추정하고자 하므로 인자 수가 5개일 때는 $$ 2_{\mathrm{V}}^{5-1}$$ 부분요인배치법을 이용하였다. <Table 1>의 실험 횟수는 중앙점 개수까지 포함한 것으로서, 인자 수가 2에서 5까지 증가함에 따라 중앙점의 수는 전체 실험영역의 예측분산 균일성을 확보하기 위해 각각 5, 6, 7, 6개로 정하였다(Myers et al., 2016). 설계최적화기준 값 비교 결과는 <Figure 5>에 시각적으로 나타내었다.

Figure 5.

Design Optimality Comparison between CCD and OFAT

4. 사례 데이터를 이용한 비교

본 논문에서 제안한 방법과 OFAT 실험방법을 실제 사례에 적용하여 비교하기 위해 Derringer and Suich(1980)의 타이어 트레드 화합물(Tire Tread Compound)의 경도(Hardness) 최적화 실험데이터를 이용하였다. 인자는 하이드레이티드실리카(Hydrated Silica, X₁), 실란 커플링제(Silane Coupling Agent, X₂), 황(Sulfur, X₃)이며, 각 인자의 수준은 <Table 2>와 같다. 실험데이터를 분석하여 얻은 모형식의 성능을 나타내는 지표로는 평균제곱오차 제곱근(Root Mean Squared Error; RMSE)과 $$ R_{adj}^2$$(수정된 결정계수)를 사용했으며, 각 성능지표의 계산식은 식 (11)과 (12)에 나타냈다. 여기서 p는 모형식에 포함된 항의 개수이다.

Table 2.

Factors and Levels of the Tire Tread Compound Experiment

RMSE는 실제값과 예측값 차이의 제곱평균인 MSE(평균제곱오차)의 제곱근으로서, 이것은 작을수록 좋다. $$ R_{adj}^2$$는 수정된 결정계수로서, 모형식에 유의하지 않은 항이 추가되더라도 값이 커지는 R²(결정계수)의 단점을 보완하는 지표이다. $$ R_{adj}^2$$는 모형에 의미가 없는 항이 추가되면 그 값이 감소하므로 이것을 크게 하는 방향으로 항을 포함하거나 제외한다.

<Table 3 (a)>는 Derringer and Suich(1980) 논문의 데이터 중에서 2수준 요인배치와 중앙점 반복 데이터 3개로 이루어진 것이다. 이를 분석한 결과, 곡률효과 항의 P-값이 0.009로 매우 작아 곡률효과가 있음을 확인했다. 따라서 축점 6개와 중앙점 3개를 추가하면(<Table 3 (b)>), 중심합성계획의 설계행렬이 된다. 20개 실험데이터를 분석하여 RMSE는 가장 작고 $$ R_{adj}^2$$가 가장 크게 나타난 식은 (13)과 같다. 식 (13)의 RMSE와 $$ R_{adj}^2$$는 각각 1.137, 93.6%이다.

Table 3.

Central Composite Design Matrix and Hardness Data of the Tire Tread Compound Experiment

OFAT를 적용하기 위하여 구성한 실험데이터는 식 (13)에 이 모형식의 RMSE 값을 이용하여 N(0, 1.137²)에서 랜덤하게 생성된 오차를 추가하여 만들고, 중앙점 반복 데이터는 <Table 3>의 6개 데이터를 그대로 이용하였다. 설계행렬과 반응변수 값은 <Table 4>에 나타냈다. 30개 데이터를 분석하여 RMSE와 $$ R_{adj}^2$$ 바탕으로 구성한 모형식은 식 (14)와 같다.

Table 4.

One-Factor-At-a-Time Design Matrix and Hardness Data of the Tire Tread Compound Experiment

모형식 성능 비교 결과는 <Table 5>에 정리하였는데, 중앙점 추가 요인배치 실험을 하고 이후 축점과 중앙점을 추가하여 중심합성계획으로 통합된 실험방법이 더 우수하다는 것을 알 수 있다.

Table 5.

Model Performance Comparison between CCD and OFAT Experiments of the Tire Tread Compound Experiment

5. 토의 및 결론

2^k 요인배치에 중앙점을 추가하는 실험은 곡률효과 존재 여부 파악과 실험오차 추정을 위해 주로 사용되었으나, 본 연구에서는 이를 현행 공정개선에 활용할 수 있음을 제안하였다. 이 방법의 우수성을 설명하기 위해 기존 공정을 개선하는 데 사용하는 한번에 한인자(OFAT) 실험방법과 비교하였는데, 중앙점 추가 2수준 요인배치와 축점을 추가한 실험방법이 설계최적화기준, 실험영역의 범위, 실험횟수, 교호작용 추정 측면에서 우수했으며, 사례를 통해 이를 확인하였다.

제품과 공정의 현행 조건을 개선하여 반응변수를 최적화하고자 할 때, 중앙점 추가 2수준 요인배치 실험방법을 활용할 것을 제안한다. 이 방법을 이용하면 적은 수의 실험으로도 넓은 범위의 영역을 탐색하고 프로세스를 더 정확하게 이해할 수 있어서 실험의 경제성과 효과성을 높일 수 있다.

References

• Derringer, G. and Suich, R. (1980), Simultaneous Optimization of Several Response Variables, Journal of Quality Technology, 12(4), 214-219. [https://doi.org/10.1080/00224065.1980.11980968]
• Knowlton, J. and Keppinger, R. (1993), The Experimental Process, Quality Progress, February, 43-47.
• Myers, R. H., Montgomery, D. C., and Anderson-Cook, C. M. (2016), Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th Ed., John Wiley & Sons, NJ.
• Wu, C. F. J. and Hamada, M. S. (2009), Experiments: Planning, Analysis, and Optimization, 2nd Ed., John Wiley & Sons, NJ.