반도체 제조 공정 소재 품질을 위한 멀티모달 이상 탐지
© 2025 KIIE
Abstract
In the semiconductor industry, as processes continue to miniaturize, monitoring material quality has become increasingly critical. Traditional methods, which largely rely on statistical analysis and expert-driven heuristics, are time-consuming and costly. This study introduces an approach using a multimodal structure combined with autoencoders to incerease the efficiency of the monitoring process, leading to reductions in both time and cost. The proposed method uses both time series and image data, which are transformed from raw semiconductor process material data through the Markov transition field technique. By integrating masking into the input data, processed separately by distinct autoencoders, the system effectively extracts and concatenates features. These are subsequently passed through a self-attention layer and reconstructed by each decoder to train the model. Experimental results demonstrate that the proposed multimodal approach significantly enhances anomaly detection capabilities, outpeforming traditional methods. The findings suggest substantial improvements in the efficiency and accuracy of quality monitoring in semiconductor manufacturing processes.
Keywords:
Semiconductor Process, Material Quality Monitoring, Multi-Modal Deep Learning, Anomaly Detection, Autoencoder, Masking, Self-attention1. 서 론
반도체는 모바일 기기부터 자동차에 이르기까지 다양한 산업 분야에서 기술 발전과 함께 그 중요성이 점점 커지고 있으며, 시장 규모도 지속적으로 성장하고 있다. 최근 반도체 공정의 주요 동향 중 하나는 반도체 칩의 회로 선폭을 극도로 미세화 하는 것이다(Park et al., 2010). 공정이 미세화 될수록 소재 품질의 중요성은 더욱 커지며, 이는 반도체 공정에서 매우 중요한 요소로 작용한다. 소재 품질은 소재 단면적에 포함된 불순물 크기와 개수를 의미하는데, 같은 크기의 불순물이라도 회로 선폭이 작아질수록 불량을 유발할 가능성이 높아져 엄격한 품질 관리가 요구된다. 따라서 반도체 공정에서 소재 품질을 지속적으로 모니터링하여 품질 이슈를 조기에 감지하는 것은 제품의 최종 수율을 결정짓는 핵심 역량이라고 할 수 있다(Baek et al., 2023; Shin et al., 2022).
기존 반도체 산업에서 인공지능 기법을 사용한 연구에서는 주로 웨이퍼 표면을 주사전자현미경으로 측정하거나 구조를 투과전자현미경으로 측정한 이미지 데이터, 반도체 공정 설비에서 수집된 온도, 압력, 전력 등의 센서 데이터 및 공정 후 수율 데이터 그리고 EDS(energy dispersive spectroscopy) 데이터 등을 활용하고 있다(An et al., 2022; Shin et al., 2000; Hwang et al., 2023). 반도체 공정에서 소재의 전기적 특성을 평가하거나 표면 결함, 또는 화학적 반응을 연구하는 데에도 인공지능 기법을 적용하고 있으나(Deen et al.,2017; Chien et al., 2020; O’Leary et al., 2020), 소재 품질 데이터에 인공지능 기법을 적용한 연구는 아직 이루어지지 않았다. 앞서 언급한 것처럼 최근 반도체 공정의 미세화가 진행됨에 따라 소재 품질의 중요성이 더욱 부각되고 있어, 해당 분야에 대한 연구가 시급히 필요한 실정이다. 반도체 제조 공정에서 소재 품질 불량을 가장 먼저 감지할 수 있는 기본 장치는 모니터링 시스템이다. 그러나 현장에서는 여전히 작업자들이 직접 눈으로 판별하는 휴리스틱한 방법에 의존하는 경우가 많다(Kim et al., 2024). <Figure 1>은 반도체 공정 중 소재 품질 데이터 수집을 위한 프로세스의 예시를 보여주고 있다. 이 프로세스에서는 각 공정마다 발생하는 수많은 품질 이상 계측 데이터를 작업자가 직접 모니터링 해야 하며, 최근 반도체 공정 미세화로 품질 기준이 엄격해지면서 작업자가 모니터링 해야 하는 데이터 양도 급증하고 있다. 수천 개의 소재 공정에서 발생하는 수만 개의 계측 데이터를 모두 눈으로 확인하는 것은 사실상 불가능하며, 그로 인해 이상치를 탐지하지 못하는 경우가 빈번하게 발생한다(Choi et al., 2024). 이는 결과적으로 시간과 비용을 초래하는 불량 처리 문제로 이어지게 된다. 이에 본 연구에서는 이러한 문제를 해결하기 위해 인공지능 기반 이상 탐지 알고리즘을 반도체 공정의 소재 품질 모니터링에 적용하고자 한다.
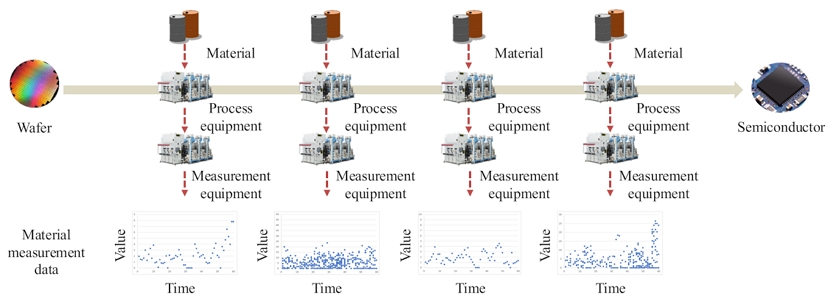
An Example of the Data Collection Process for Measuring Material Quality During the Semiconductor Process
본 연구에서 분류 알고리즘 대신 이상 탐지 알고리즘을 적용하려는 주된 이유는 클래스 불균형 문제 때문이다. 반도체 산업과 같은 제조 산업에서 수집되는 데이터는 정상 데이터가 대부분을 차지하며, 비정상 데이터는 매우 적어 클래스 불균형이 발생한다(Michau et al., 2020). 이와 같은 상황에서는 정상/불량 클래스 정보를 활용한 분류 모델을 이용하는 것보다, 정상 데이터만을 사용해 모델을 학습시키고 이상을 탐지하는 방식이 실제 현장에 더 적합하고 효과적이다(Pang et al., 2021). 본 연구에서는 기존 이상 탐지 머신러닝 모델인 LOF(local outlier factor; Susto et al., 2017), OC-SVM(one-class support vector machine, Li et al., 2003), IForest(isolation forest; Susto et al., 2017)를 적용하여 성능을 확인한 후, 오토인코더(autoencoder; Chen et al., 2018) 기반의 딥러닝 모델을 차례로 적용해 그 성능을 검증하였다. 특히, 시계열 데이터와 변환된 이미지 데이터를 멀티모달 입력으로 사용하는 MTIMA(multimodal with time series and image data, masking, attention) 모델을 제안하여 기존 비교 방법론 중 가장 높은 anomaly transformer보다 이상 탐지 성능을 3.8% 더 향상시켰다. 반도체 공정 소재 품질 데이터를 활용한 이상치 탐지 접근 방식은 이 분야에서 처음으로 시도되는 연구이며, 시계열 데이터를 이미지 데이터로 변환하여 멀티모달 입력으로 동시에 활용하는 이상 탐지 방법론 또한 독창적인 아이디어라고 할 수 있겠다. 제안 방법론은 정상 데이터만을 이용해 학습하며, 입력과 출력 간의 재구축 오차를 이용해 이상 여부를 판단하는 오토인코더 기반이다. 이미지 데이터로의 변환에는 마르코프 전이 필드(Markov transition fields, MTF) 변환을 적용하였으며, 어텐션 메커니즘(attention mechanism; Vaswani, 2017)을 추가하여 중요한 정보의 학습을 강화하였다. 또한 마스킹(masking; He et al., 2022) 기법을 사용하여 입력 데이터의 일부를 임의로 가림으로써 부분적인 정보만으로도 전체 패턴을 학습할 수 있도록 하여 모델의 강건성을 높였다. 본 연구의 주요 기여점은 다음과 같다.
- 1) 본 연구는 반도체 공정에서 발생하는 소재 품질 불량 계측 데이터에 대해 이상 탐지 방법론을 처음으로 적용한 사례로, 기존 휴리스틱한 모니터링 방법의 한계를 극복하고 실험을 통해 제안된 방법론의 우수한 성능을 입증했다.
- 2) 제안 방법론은 시계열 데이터와 이를 변환한 이미지 데이터를 동시에 학습에 이용하는 멀티모달 구조를 활용함으로써 기존 방법론에 비해 더 뛰어난 성능을 보였다.
- 3) 마스킹과 어텐션 레이어를 제안된 MTIMA 구조에 결합하여, 모델의 강건성을 높이는 동시에 중요한 정보를 효과적으로 학습시켜 성능을 향상시킬 수 있음을 입증하였다.
2. 배경 이론
반도체 제조 분야에서의 이상 탐지는 품질 관리와 수율 향상을 위한 핵심적인 과제로, 제품 품질 저하나 공정 실패를 조기에 감지하여 생산성을 높이고 비용을 절감하는 데 중요한 역할을 한다. 이상 탐지 알고리즘은 크게 머신러닝 기반 방법, 딥러닝 기반 방법으로 나눌 수 있다. 머신러닝 기반 방법에는 LOF, OC-SVM, IForest 등이 포함되며, 이들은 데이터의 패턴을 학습하여 정상과 이상을 구분한다. 최근에는 오토인코더, LSTM, GAN(Hosseinpour et al., 2022; Xia et al., 2022) 등의 딥러닝 모델을 이용한 이상 탐지 방법이 주목받고 있으며, 이들은 복잡한 비선형 패턴을 학습할 수 있어 시계열 및 이미지 데이터에서 효과적이다. 특히 USAD(unsupervised anomaly detection; Audibert et al., 2020)는 적대적 훈련 개념을 오토인코더에 적용하여 이상 탐지 성능을 향상시킨 모델로, 재구축과 판별의 균형을 통해 효과적인 이상 탐지를 수행한다. 또한 anomaly transformer(Xu et al., 2021)는 트랜스포머 구조를 기반으로 하여 시계열 데이터의 장기 의존성을 포착하고 연관성 기반의 이상 탐지를 수행하는 최신 모델이다. 이러한 다양한 방법론의 발전은 반도체 제조 공정에서 이상 탐지 성능을 지속적으로 개선하고 있으며, 보다 정확하고 효율적인 품질 관리 시스템의 구축을 가능하게 하고 있다. 하지만 본 연구의 목적인 반도체 공정 소재 품질 관리를 위한 이상 탐지를 수행한 연구는 아직 보고된 바가 없다. 또한 그 동안 여러 연구에서 멀티모달 구조를 활용한 이상 탐지 방법론에 대한 연구를 진행하였으나, 시계열 데이터를 이미지 데이터로 변환하여 동시에 멀티모달 입력으로 사용하는 방법론에 대한 연구는 없었다. 따라서 본 연구에서는 멀티모달 데이터를 입력으로 사용함으로써 정보의 다양성을 높이고 성능을 극대화하고자 한다(Radoi, 2022; Rahim et al., 2023).
오토인코더는 비지도 학습 신경망 모델로, 입력 데이터를 압축하고 다시 복원하는 과정을 통해 데이터의 중요한 특징을 학습한다. 오토인코더의 구조는 일반적으로 인코더(encoder), 잠재 공간(latent space), 디코더(decoder)로 구성되며, 인코더는 입력 데이터를 저차원의 잠재 벡터로 압축하고, 디코더는 이 잠재 벡터를 원래의 입력 차원으로 복원한다. 정상 데이터만을 사용하여 학습하며, 이 과정에서 입력과 출력 간의 차이를 최소화하는 방향으로 파라미터를 조정한다. 이렇게 학습된 오토인코더는 정상 데이터의 패턴은 잘 재구축할 수 있지만, 이상 데이터에 대해서는 높은 재구축 오차를 보이게 된다. 따라서 새로운 데이터에 대한 재구축 오차가 특정 임계값을 초과할 경우, 해당 데이터를 이상으로 판단할 수 있다. 이러한 접근 방식은 특히 고차원 데이터나 복잡한 패턴을 가진 데이터에서 효과적이며, 레이블이 없는 데이터에서도 이상을 탐지할 수 있다는 장점이 있다. 따라서 레이블 비용이 높고, 이상치가 적은 현업에서 적합한 방법이 될 수 있다.
마스킹과 셀프 어텐션 메커니즘(self-attention mechanism)은 최근 딥러닝 모델의 성능을 크게 향상시킨 기법들이다. 마스킹은 입력 데이터의 일부를 임의로 가리는 기법으로, 모델의 강건성을 향상시키고 과적합을 방지하는 데 도움을 준다. 이는 모델이 부분적인 정보만으로도 전체 패턴을 학습하도록 유도하며, 특히 시계열 데이터나 이미지 데이터에서 효과적이다. 마스킹은 학습 과정에서 무작위로 적용되며, 이를 통해 모델은 다양한 입력 시나리오에 대해 견고한 성능을 보일 수 있게 된다. 한편, 셀프 어텐션은 데이터의 각 시점이나 특징에 대해 동적으로 가중치를 부여함으로써, 중요한 패턴이나 특징에 더 집중할 수 있게 하는 방법으로, 특히 트랜스포머 모델에서 핵심적인 역할을 한다. 셀프 어텐션은 입력 시퀀스의 모든 요소 간 관계를 고려하여 각 요소의 중요도를 계산하므로, 국소적으로 중요한 특징뿐만 아니라 전역적으로 중요한 패턴도 효과적으로 포착할 수 있다(Li et al., 2020). 본 연구는 이 두 가지 요소를 제안 방법론에 접목시킴으로써 이상 탐지 성능을 향상시키고자 한다.
3. 제안 방법론
3.1 멀티모달 데이터 생성
먼저, 반도체 공정 중 소재 품질 계측 데이터의 이상을 효과적으로 탐지하기 위해 MTF 기반의 이미지 변환 기법을 적용하였다(Garcia et al., 2022). 이 방법은 시계열 데이터를 2차원 이미지로 변환하여, 테이블 형태의 시계열 데이터와 함께 멀티모달 입력으로 활용함으로써 이상 탐지 성능을 향상시키는 것을 목적으로 한다. MTF 변환을 통한 이미지화는 단순히 시각화를 위한 것이 아니라, 데이터의 동적 전이 정보를 얻기 위한 것이다. MTF는 전역적 및 국소적 패턴 포착, 장단기 시간 의존성 표현, 시계열 정보 보존 등의 특성을 가지고 있어서 시계열 데이터를 MTF 이미지로 변환하는 것은 테이블 형태의 데이터만을 사용하는 것보다 더 풍부한 정보를 제공할 수 있다.
멀티모달 데이터 생성 작업은 데이터 전처리, 데이터 이산화, 전이 확률 계산, 마르코프 전이 행렬 생성의 단계로 구성된다. 먼저, 원본 소재 품질 계측 시계열 데이터에 대한 전처리 과정을 수행한다. 이 과정에서는 결측치 처리, 이상치 제거, 통계량 추출을 통해 원본 데이터의 특성을 효과적으로 표현할 수 있도록 테이블 형태의 시계열 데이터 XT로 정규화 한다. 자세한 전처리 과정과 그 효과는 실험 및 결과 섹션에서 상세히 기술한다.
이렇게 전처리 된 시계열 데이터 XT에 대해 MTF 변환을 적용한다. MTF 변환은 시계열 데이터를 이산화 하여 전이 확률을 계산하는 알고리즘이다(Wang et al., 2015). 먼저, 시계열 데이터 의 모든 샘플 에 대해 동등하게 Q개의 구간으로 나누고, 각 나눠진 시계열 데이터 값은 특정 구간 qj(j∈([1,Q]))에 해당된다. 1차 마르코프 체인을 통해 Q×Q크기의 마르코프 행렬 W를 식 (1)과 같이 구성한다.
| (1) |
| (2) |
식 (1)에서 wij=P{xt+1∈qi|xt∈qj}는 현재 t 시간일 때 데이터 xt가 구간 qj에 속해 있을 때, 다음 시간에 구간 qi에 나타날 확률을 의미한다. 확률 값의 범위는 (0,1)이며 각 열의 합은 식 (2)와 같이 1을 만족한다. 그러나, 이 마르코프 행렬 W는 시간에 따른 변화를 포착하지 못하므로, 이를 시간 축에 따라 Q개 구간으로 나눔으로써 식 (3)과 같이 MTF 행렬로 확장한다(Wang et al., 2022).
| (3) |
wij|xn∈qi, xn∈qj는 구간 qi에서 qj로의 전이 확률을 나타내며, 시간 i와 j에 있는 데이터 xn은 각각 구간 qi와 qj에 속한다. 이를 통해 MTF 행렬은 다양한 시간 척도에서의 상태 전이 패턴을 포착하며, 시계열 데이터의 시간적 구조와 동적 특성을 종합적으로 표현한다. 이러한 MTF 변환 방식은 단순한 연속 시간 단계 간의 전이 뿐 아니라 더 긴 시간 간격에 걸친 상태 변화도 효과적으로 분석할 수 있게 해준다. 이렇게 생성된 MTF 행렬은 최종적으로 <Figure 2>와 같이 시계열 데이터를 이미지로 시각화 해준다. 이로써 데이터의 특성을 전이 확률의 강도와 패턴을 통해 시각적으로 표현할 수 있다.
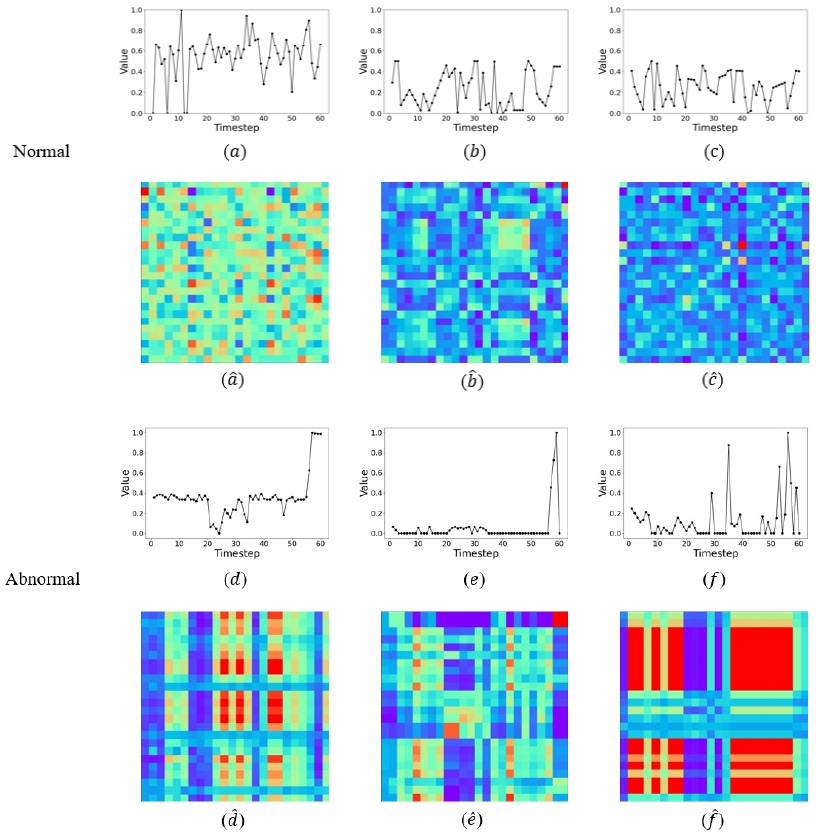
(a), (b), and (c) Represent Normal Time Series Data, and (a^), (b^), and (c^) are the Corresponding MTF-Transformed Images. (d), (e), and (f) Represent Abnormal Time Series Data, and (d^), (e^), and (f^) are the Corresponding MTF-Transformed Images
<Figure 2>는 정상 데이터와 비정상 데이터의 시계열 데이터를 MTF로 변환한 이미지를 비교하여 보여주는 결과이다. (), (), ()는 정상 데이터의 MTF 이미지로, 전반적으로 균일한 색상 분포와 부드러운 전이 패턴을 보여준다. 특히, ()의 경우 밝은 녹색이 지배적이며 다양한 색상의 픽셀들이 고르게 분포되어 있어 다양한 상태 전이가 일어나는 안정적인 상태를 나타낸다. ()와 ()은 파란색과 청록색이 주를 이루며 전반적으로 균일하게 나타나 일관성 있고 안정적인 시계열의 특성을 보여준다. 반면, (), (), ()는 비정상 데이터의 MTF 이미지로 정상 데이터와 뚜렷한 차이를 보인다. ()의 경우 매우 강한 수직 패턴과 뚜렷한 빨간색 영역이 나타나며, 청록색 수평선이 이미지를 가로지르고 있다. 이는 특정 상태로의 강한 전이와 비정상적인 패턴을 나타낸다. ()은 불규칙한 블록 패턴과 산발적으로 분포된 빨간색 픽셀들이 특징적이며, 이는 급격한 상태 변화와 불안정한 상태를 의미한다. ()은 매우 뚜렷한 격자 패턴과 큰 빨간색 및 보라색 영역이 나타나며, 중앙의 청록색 십자 모양 패턴이 특징적이다. 이는 극단적으로 구조화된 패턴으로, 매우 비정상적인 시계열 특성을 나타내고 있다. 이렇게 MTF 이미지 변환 방법은 시계열 데이터의 동적 특성을 효과적으로 포착하고 시각화 할 수 있다. MTF는 전역적 및 국소적 패턴을 동시에 포착하며, 비선형성과 장기 의존성을 2차원 공간에 매핑한다. 또한, 점진적인 변화를 연속적인 색상 변화로 표현하여 감지할 수도 있다. 이러한 특성들로 인해 MTF는 기존의 1차원 시계열 분석 방법으로는 포착하기 어려운 패턴을 드러낼 수 있기 때문에 컨볼루션 신경망(convolutional neural networks)을 통한 이상 탐지 작업의 성능을 향상시킬 수 있다.
3.2 제안 방법론 전체 구조
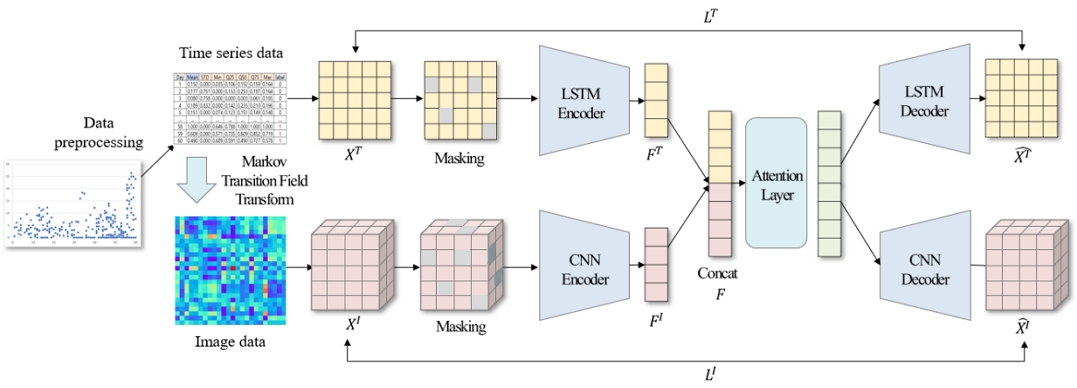
제안 방법론 MTIMA의 전체 구조는 Figure 3에 나타나 있다. MTIMA는 크게 인코더, 셀프 어텐션 레이어, 디코더로 구성된다. Figure 3에서 볼 수 있듯이 제안 방법론은 하나는 시계열 데이터 XT를, 다른 하나는 이미지 데이터 XI인 멀티모달로 입력을 받는다. 인코더 부분은 LSTM 인코더와 CNN 인코더로 나뉘어 각각 시계열 데이터와 이미지 데이터를 처리하고, 각 인코더는 입력 데이터를 특징 벡터 FT와 FI로 변환한 뒤에 두 벡터를 결합하여 F를 생성한다. 그리고 이 결합한 특징 벡터 F를 셀프 어텐션 레이어에 통과시킨다. 이때, F의 어텐션 결과는 식 (4)와 같이 표현할 수 있다(Vaswani, 2017).
| (4) |
여기서 A는 가중치 분포 행렬로 다음 식 (5)와 같이 정의된다.
| (5) |
는 어텐션 스코어 행렬로 다음 식 (6)과 같다.
| (6) |
여기서 WV, WQ, WK는 파라미터 행렬이고, dz는 FWK의 차원을 나타내며 내적 값이 차원에 따라 증가하지 않도록 방지하는 스케일링 값이다. 이 셀프 어텐션 레이어의 역할은 모든 벡터 간 가중치를 계산할 때, 연관성이 높을수록 값이 커지게 되므로 상호작용이 중요한 정보를 더 강하게 학습하게 한다. 디코더 부분은 <Figure 3>의 오른쪽에 표시된 대로 LSTM 디코더와 CNN 디코더로 구성되어 있으며, 셀프 어텐션 레이어의 출력을 받아 LSTM 디코더는 원래의 시계열 데이터 형태로, CNN 디코더는 이미지 데이터 형태로 복원한다.
제안 방법론의 강건성을 향상시키기 위해 입력 데이터에 마스킹 기법을 적용하였다. 이는 일부 입력 값을 임의로 가리는 방식으로, 학습 시에 가려진 부분의 주변 정보를 사용하여 예측하면서 특징을 추출하고 복원하게 함으로써 모델이 더 강건 해진다. 마스킹 된 데이터는 식 (7), (8)과 같이 표현할 수 있다.
| (7) |
| (8) |
여기서 MT와 MI는 각각 시계열 데이터와 이미지 데이터에 대한 마스크이고, ⊙는 요소별 곱셈을 하는 합성곱을 나타낸다. 제안 방법론의 학습을 위해 평균 제곱 오차(mean squared error, MSE)를 기반으로 한 손실 함수를 사용하였다. <Figure 3>에 표시된 LT와 LI가 이에 해당하며 전체 손실 함수는 식 (9)와 같으며, 이는 식 (10), (11)과 같이 표현된 시계열 데이터와 이미지 데이터의 재구축 오차의 합으로 계산된다.
| (9) |
| (10) |
| (11) |
여기서 XT와 XI는 각각 원본의 시계열 데이터와 이미지 데이터를 나타내며, 와 는 각각 재구축된 시계열 데이터와 이미지 데이터이다. n과 m은 각 데이터의 차원을 나타낸다. 학습된 모델을 활용한 이상 탐지는 새로운 데이터 샘플에 대한 재구축 오차를 기반으로 이상 탐지 점수를 계산하는 방식으로 이루어진다. 이때 재구축 오차가 미리 정의된 임계값 θ를 초과하면 해당 샘플을 이상으로 판단한다. 이를 식 (12)와 같이 표현할 수 있다.
| (12) |
여기서 는 입력 데이터 X와 재구축된 데이터 사이의 손실을 나타낸다.
Algorithm 1은 제안된 MTIMA의 순차적인 학습 과정을 의사 코드(pseudo code)로 나타낸 것이다.
4. 실험 및 결과
4.1 데이터 셋 및 평가 지표
본 연구에서는 국내 반도체 기업 12인치 공정 중 소재 품질 계측 데이터를 기반으로 하였다. 수집된 데이터 샘플 수는 12,754개이며 각 샘플은 60개의 시간 단위(timestep)로 이루어져 있다. 이 중 정상 데이터는 12,499개(98%)이고, 이상 데이터는 255개(2%)이며, 훈련용(72%), 검증용(18%), 평가용(10%) 데이터로 분할하여 모델 학습 및 성능 검증에 활용하였다. 원본 데이터는 단일 계측 수치로 구성된 단변량 데이터이며, 레이블, 시간, 샘플 번호의 정보와 함께 제공된다. 특히, 각 시간 단위별로 관측되는 계측 값의 수가 불규칙하여 직접적인 학습 입력으로 사용하기 어려운 특성이 있었다. 이를 멀티모달 학습에 적합한 두 개의 모달리티로 변환하기 위해 다음과 같은 전처리 과정을 수행하였다. 우선 결측치는 앞뒤 값의 선형 보간법을 통해 산출된 데이터로 대체하였고, 데이터의 신뢰성을 확보하기 위해 전체 데이터 중 크기 기준 상위 10%를 이상치로 분류하여 제거하였다. 각 시간 단위별로 관측되는 불규칙한 계측 값들을 균일한 형태로 변환하기 위해, 각 시점에서 평균(mean), 표준편차(std), 최대값(max), 최소값(min), 사분위수(25%, 50%, 75%)의 7개 통계량을 추출하였다. 이는 시간 단위별로 발생하는 다수의 불규칙한 관측치들을 대표할 수 있는 통계적 특성을 포착하면서도, 입력 데이터의 차원을 일정하게 유지할 수 있다. 추출된 통계량들은 최소-최대 스케일링(min-max scaling)을 적용하여 정규화 하였다. 이와 같은 전처리 과정을 거쳐 최종적으로 각 샘플 당 시간 길이 60에 7개의 변수를 가진 시계열 데이터를 생성하였으며, 첫 번째 입력 모달리티로 학습에 사용하였다. 이후 생성된 시계열 데이터를 MTF를 이용하여 이미지로 변환하였으며, 이를 두 번째 입력 모달리티로 이용하였다. 이미지 변환 방식 중에서 MTF 방식을 채택한 이유는 다양한 이미지 변환 방식(gray scale encodings, gramian angular field, recurrence plot, scalogram, Markov transition field)을 실험한 결과 가장 우수한 성능을 보였기 때문이다. <Table 1>은 시계열 데이터를 이미지로 변환하는 데 널리 사용되는 다섯 가지 방법의 실험 결과를 제시하고 있다. 이 실험 결과를 통해 MTF 방식이 다른 방법들에 비해 뛰어난 성능을 나타냄을 확인할 수 있었다.
Average Performance and Standard Deviations (in Parentheses) for Different Encoding Methods, Presented in Terms of Precision, Recall, and F1-Score. The Best Results for Each Performance Metric are Highlighted in Bold
평가 지표로는 정밀도(precision), 재현율(recall), F1 점수(F1-score)를 사용했다. 정밀도는 모델이 ‘true’라고 분류한 것 중 실제로 ‘true’인 데이터의 비율을 나타내며, 식 (13)로 계산된다. 정밀도가 높다는 것은 모델이 false positive를 적게 분류했음을 의미하며, 이는 모델이 정상으로 판단한 데이터가 실제로 정상일 확률이 높음을 뜻한다. 재현율은 실제 ‘true’인 데이터 중에서 모델이 ‘true’로 올바르게 분류한 비율을 나타내며, 식 (14)으로 계산된다. 재현율이 높다는 것은 모델이 false negative를 적게 분류했음을 의미하며, 실제로 비정상인 데이터를 대부분 올바르게 비정상으로 분류할 가능성이 높다는 것을 뜻한다. F1 점수(F1-score)는 정밀도와 재현율의 조화 평균으로, 식 (15)로 계산되며, 점수가 높을수록 모델의 전반적인 성능이 우수하다고 판단할 수 있다. 특히, 클래스 간 불균형이 심한 데이터에서 F1 점수는 모델 성능을 평가하는 데 널리 사용되는 지표이다.
| (13) |
| (14) |
| (15) |
여기서 TP는 모델이 이상 클래스를 올바르게 이상으로 분류한 경우이며, TN은 모델이 정상 클래스를 올바르게 정상으로 분류한 경우를 뜻한다. FP는 모델이 정상 클래스를 이상으로 잘못 분류한 경우이고, FN은 모델이 이상 클래스를 정상으로 잘못 분류한 경우를 의미한다.
4.2 실험 조건
본 연구에서 제안한 방법론과 비교 방법론에 사용된 딥러닝 모델들을 30 에포크(epoch) 동안 학습시켰고, 최적화 알고리즘으로는 Adam(adaptive moment estimation)을 사용했다. 학습률(learning rate)은 0.001로 설정했고, 배치 사이즈(batch size)는 64로 적용했다. 제안 방법론의 성능 평가의 통계적 신뢰성과 일관된 성능을 확보하기 위해 모든 실험을 무작위 시드값으로 5회 반복 수행하였다. 각 실험에서는 전체 데이터 중 20%를 검증 세트로 분할하여, 서로 다른 훈련 / 검증 세트 구성으로 평가를 진행하였으며, 이를 통해 모델 성능 지표의 평균과 표준편차를 산출하였다. 모든 실험은 NVIDIA A100-SXM4-40GB GPU 환경에서 수행되었으며, 데이터 전처리를 제외하고 1회 훈련에 약 300초(30 에포크 기준)가 소요되었다. <Table 2>는 제안 방법론인 MTIMA의 전체 구조를 세부적으로 정리한 것이다. 주요 구성 레이어와 각 레이어의 출력 형태 및 흐름을 포함하여 실험에 사용된 구조를 체계적으로 설명하고 있다.
4.3 결과
<Table 3>은 반도체 공정 중 소재 품질 계측 데이터에 대한 이상 탐지를 위해 다양한 모델을 적용한 실험 결과를 보여주고 있다. 결론적으로 제안 방법론인 MTIMA가 모든 평가 지표(정밀도, 재현율, F1 점수)에서 비교 방법론에 비해 가장 높은 성능을 보였다. 실험 설계는 전처리한 시계열 데이터와 이미지 데이터를 각각 비교 방법론에 대해 적용한 후, 이 두 가지 데이터를 모두 입력으로 사용하는 멀티모달 입력방식의 MTIMA를 평가하는 방식으로 진행하였다. 먼저 시계열 데이터만을 입력 모달리티로 사용한 실험 결과를 살펴보면, 전통적인 머신러닝 기반 이상 탐지 모델인 LOF, OC-SVM, IForest는 모두 F1 점수가 0.7대에 머물렀다. 이는 비교적 낮은 성능으로, 머신러닝 기반 모델들은 복잡한 반도체 공정 데이터의 특성을 충분히 포착하지 못했음을 의미한다. 반면, 딥러닝 기반 모델인 autoencoder, variational autoencoder, LSTM autoencoder는 F1 점수가 0.8대로, 전통적인 모델들보다 우수한 성능을 보였다. 이는 딥러닝 모델이 데이터의 복잡한 패턴을 학습하는 데 더 효과적임을 시사한다. 특히 LSTM autoencoder는 시계열 데이터의 시간적 의존성을 잘 포착하여 가장 높은 성능을 보였다. 또한 최신 모델인 USAD와 anomaly transformer는 시계열 데이터를 입력 모달리티로 사용한 실험에서 가장 높은 F1점수를 기록했다. 특히, anomaly transformer 모델은 F1 점수 0.926을 달성하여, 제안 방법론 MTIMA 다음으로 높은 성능을 보였다.

Average Performance and Standard Deviations (in Parentheses) for Ten Models Based on Input Data Types, Presented in Terms of Precision, Recall, and F1-Score. The Best Results for Each Performance Metric are Highlighted in Bold
시계열 데이터를 MTF 이미지로 변환하여 CNN autoencoder 모델에 입력 데이터로 실험했을 때, F1 점수는 0.870으로 나타났으며, 이는 시계열 데이터에 대한 LSTM autoencoder와 동일한 성능이다. 이를 통해 최신 모델인 USAD와 anomaly transformer보다는 성능이 낮지만, 여전히 충분히 경쟁력 있는 성능을 보임을 확인할 수 있다. 제안방법론인 MTIMA는 시계열 데이터와 이미지 데이터를 동시에 활용한 멀티모달 접근 방식을 통해 F1 점수 0.961을 달성하였다. 이는 모든 비교 방법론 중 가장 높은 성능으로, 두 번째로 높은 성능을 보인 anomaly transformer보다 3.8% 더 우수했으며, 이미지 데이터만을 이용한 CNN autoencoder와 비교했을 때는 무려 10.5%의 성능 향상을 보여준다. MTIMA의 이러한 우수한 성능은 멀티모달 접근 방식의 효과성을 입증하며, 서로 다른 유형의 데이터에서 추출된 정보를 효과적으로 결합하는 것에 대한 효용성을 보여 준다.
5. 논의
제안 방법인 MTIMA의 우수한 성능이 어떤 구성 요소들에 기인하는지 체계적으로 분석하고, 강건성을 정량적으로 평가하기 위한 실험들을 진행하였다.
<Table 4>는 제안 방법론인 MTIMA의 주요 구성 요소인 셀프 어텐션 레이어와 마스킹이 전체 성능에 미치는 영향도를 분석하기 위한 절제 연구 결과를 보여준다. 실험 결과, MTIMA는 0.980의 정밀도, 0.943의 재현율, 0.961의 F1 점수로 모든 성능 지표에서 가장 우수한 성능을 보였다. 셀프 어텐션 레이어를 제거한 모델(MTIMA w/o self-attention layer)의 경우 F1 점수가 0.912로 5.1% 감소했다. 이는 셀프 어텐션 메커니즘이 시계열 데이터와 이미지 데이터 간의 중요한 관계를 포착하고, 각 벡터 간의 중요도를 효과적으로 학습함으로써 제안 방법론의 성능을 크게 향상시킨다는 것을 보여준다. 셀프 어텐션 레이어는 특히 시계열 데이터의 시간적 특징과 이미지 데이터의 공간적 특징을 효과적으로 통합하는 데 중요한 역할을 한 것으로 분석된다. 마스킹을 제거한 모델(MTIMA w/o masking)의 경우 F1 점수가 0.926으로 3.6% 감소했다. 이 결과는 마스킹 기법이 제안 방법론의 강건성을 높이는 데 기여함을 나타낸다. 마스킹은 입력 데이터의 일부를 임의로 가려, 부분적인 정보만으로도 전체 패턴을 학습할 수 있게 하며, 이는 실제 환경에서 발생할 수 있는 결측치에 대한 대응 능력을 향상시킨다. 마지막으로, 셀프 어텐션 레이어와 마스킹을 모두 제거한 모델(MTIMA w/o attention layer, masking)의 F1 점수는 0.892로, 7.2% 감소하여 가장 큰 성능 저하를 보였다. 이 결과는 두 구성 요소가 시너지 효과를 발휘하며, 제안된 방법론의 성능 향상에 중요한 역할을 한다는 것을 입증한다.

Average Performance and Standard Deviations (in Parentheses) from an Ablation Study on the Contribution of Each Component, Presented in Terms of Precision, Recall, and F1-Score. The Best Results for Each Performance Metric are Highlighted in Bold
<Table 5>는 MTIMA에서 사용된 입력 데이터 유형(시계열, 이미지)이 전체 모델 성능에 미치는 영향을 분석한 결과를 보여준다. 이 실험은 시계열 데이터와 이미지 데이터를 개별적으로 하나의 입력으로 사용하는 것에 비해 멀티모달 입력 효과를 검증하기 위해 수행되었다. MTIMA는 시계열 데이터와 이미지 데이터를 모두 사용하여 0.961의 F1 점수를 달성했다. 이미지 데이터를 제외하고 시계열 데이터만 사용한 모델(MTIMA w/o image data)은 F1 점수가 0.922로 4.1% 정도 감소했다. 이는 MTF를 통해 생성된 이미지 데이터가 원본 시계열 데이터에는 없는 추가적인 정보를 제공함을 시사한다. 시계열 데이터를 제외하고 이미지 데이터만 사용한 모델(MTIMA w/o time series data)은 F1 점수가 0.889로 7.5% 정도 크게 감소했다. 이는 시계열 데이터가 이상 탐지에 더 중요한 정보를 포함하고 있음을 나타낸다. 동시에, <Table 3>에서 USAD와 Anomaly Transformer 보다는 성능이 낮지만 하나의 입력 모달리티 만을 사용한 LSTM, CNN autoencoder 모델 실험 결과보다도 각 5.9%, 2.2% 정도 성능이 증가하여 제안 방법론 구조 자체만으로도 상당한 성능을 달성할 수 있다는 점을 보여준다. 결론적으로 <Table 5>는 시계열 데이터와 이미지 데이터가 서로 보완적인 정보를 제공하며, 두 가지 데이터 유형을 결합하는 멀티모달 접근 방식이 이상 탐지 성능을 크게 향상시킬 수 있음을 입증한다.

Average Performance and Standard Deviations (in Parentheses) from an Ablation Study on the Contribution of the Multimodal Approach, Presented in Terms of Precision, Recall, and F1-Score. The Best Results in Each Performance Metric are Highlighted in Bold.
추가적으로, 마스킹 비율을 다르게 해도 제안 방법론이 여전히 강건한 지 알아보고, 다양한 마스킹 비율에 따른 성능 비교 실험을 수행하였다. <Table 6>에서 보여주듯이 마스킹 비율을 10%에서 90%까지 10% 간격으로 변화시키며 성능을 측정한 결과, 20% 마스킹 비율에서 F1 점수 0.961로 최고 성능을 달성하였으며, 따라서 제안 방법론 마스킹 비율은 20%로 진행하였다. 주목할 만한 점은 마스킹 비율이 30%부터 성능이 점진적으로 감소하기 시작하지만, 50% 마스킹에서도 여전히 높은 성능을 유지했으며, 심지어 90%라는 극단적인 정보 손실 상황에서도 0.613의 F1 점수를 기록했다는 것이다. 이러한 결과는 제안된 방법론이 다양한 수준의 정보 손실에도 불구하고 강건한 성능을 유지할 수 있음을 입증하며, 실제 응용 환경에서 발생할 수 있는 다양한 데이터 품질 문제에 대해 효과적으로 대응할 수 있는 잠재력을 보여준다.

Average Performance from an Experimental Study on the Impact of Masking Ratios, Presented in Terms of Precision, Recall, and F1-Score. Masking Ratios Range from 10% to 90% in 10% Increments. The Best Results for Each Performance Metric are Highlighted in Bold
결국, <Table 4>~<Table 6>은 제안된 방법 MTIMA의 우수한 성능을 여러 요인에서 보여주고 있다. 첫째, 멀티모달 접근 방식을 통해 시계열 데이터와 이미지 데이터의 장점을 결합하여 더 풍부한 정보를 활용할 수 있다. 둘째, 셀프 어텐션 레이어를 통해 중요한 특징에 가중치를 부여함으로써 제안 방법론의 성능을 높였다. 셋째, 마스킹 기법을 통해 제안 방법론의 강건성을 향상시키고 과적합을 방지하였다. 이러한 요소들의 결합으로 MTIMA는 F1 점수에서 최고 성능을 보임과 동시에 높은 정밀도와 재현율을 달성하였다. 반도체 현업 전문가와 실험 결과를 검토한 결과, 제안 방법론이 실제 반도체 공정 소재 품질 모니터링에 적용 가능하다는 긍정적인 평가를 받았다.
6. 결 론
본 연구에서는 반도체 공정 중 소재 품질 계측 데이터에 대한 이상 탐지를 위한 새로운 방법론인 MTIMA를 제안하였다. MTIMA는 시계열 데이터와 이를 MTF로 변환한 이미지 데이터를 멀티모달 입력으로 사용하여 이상 탐지 성능을 향상시켰다. 실험 결과, 제안 방법론이 전통적인 머신러닝 방법과 최신 딥러닝 모델들에 비해 가장 높은 성능을 보여주었다. 이는 멀티모달 입력 방식의 효과성을 입증하는 결과로, 절제 연구를 통해 제안 방법론의 주요 구성 요소인 셀프 어텐션 레이어와 마스킹이 모두 성능 향상에 중요한 영향을 미치는 것을 확인하였다. 또한, 멀티모달 효과를 검증하기 위한 추가적인 절제 연구를 통해 단일 유형의 입력 데이터를 사용하는 것보다 멀티모달 입력 방식이 이상 탐지 성능을 크게 향상시킬 수 있음을 입증하였다. 본 연구의 주요 기여점은 반도체 공정 중 소재 품질 불량 계측 데이터에 대해 이상 탐지 방법론을 처음으로 적용하였다는 것이고, 시계열 데이터와 이미지 데이터를 동시에 사용하는 멀티모달 방식을 적용하고 이를 통해 이상 탐지 성능을 크게 향상시킨 점이다. 또한 셀프 어텐션 레이어와 마스킹을 추가한 비지도 학습 모델을 적용함으로써 강건하면서도 중요한 정보를 잘 학습하는 방법론을 개발하였다는 점을 기여점을 꼽을 수 있다. 이러한 결과는 반도체 제조 공정 소재 품질 관리에 유용한 모니터링 방법으로 제공할 수 있을 뿐만 아니라, 다른 제조 산업 분야의 품질 관리 시스템에도 적용될 수 있는 가능성을 보여준다. MTIMA의 높은 정밀도와 재현율은 실제 산업 현장에서 false positive와 false negative를 효과적으로 줄일 수 있음을 시사하며, 이는 생산성 향상과 비용 절감으로 이어질 수 있다.
본 연구의 한계는 제안 방법론에서 입력 데이터 특정 부분의 중요도를 정확히 해석하기 어렵다는 점이다. 일반적으로 어텐션 스코어를 통해 모델이 어떤 부분을 더 중요하게 고려하는지 파악하기 위해서는 인코더 입력 부분에 어텐션 레이어를 추가해야 한다. 이는 데이터가 압축되기 전에 어텐션을 적용함으로써 원본 데이터의 시점과 직접적인 연관성을 파악할 수 있기 때문이다. 그러나 제안 방법론은 이미 인코더로 압축된 특징 벡터에 어텐션 레이어를 추가했기 때문에, 원본 데이터의 어떤 부분이 결과에 더 중요하게 반영되었는지 정확히 도출하기 어렵다. 향후 연구에서는 이러한 한계점을 극복하기 위해 각 인코더에 개별적으로 어텐션 레이어를 추가하는 방식으로 변경하여 제안 방법론의 해석 가능성을 높일 것이다.
References
-
An, K. M., Shin, J. E., and Baek, D. H. (2022), Anomaly Detection Model Based on Semi-Supervised Learning Using LIME: Focusing on Semiconductor Process, Journal of Society of Korea Industrial and Systems Engineering, 45(4), 86-98.
[https://doi.org/10.11627/jksie.2022.45.4.086]

-
Audibert, J., Michiardi, P., Guyard, F., Marti, S., and Zuluaga, M. A. (2020, August), Usad: Unsupervised anomaly detection on multivariate time series, In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 3395-3404.
[https://doi.org/10.1145/3394486.3403392]

-
Baek, M. and Kim, S. B. (2023), Failure detection and primary cause identification of multivariate time series data in semiconductor equipment, IEEE Access, 11, 54363-54372.
[https://doi.org/10.1109/ACCESS.2023.3281407]

-
Chen, Z., Yeo, C. K., Lee, B. S., and Lau, C. T. (2018, April), Autoencoder-based network anomaly detection, In 2018 Wireless telecommunications symposium (WTS), IEEE, 1-5.
[https://doi.org/10.1109/WTS.2018.8363930]

-
Chien, J. C., Wu, M. T., and Lee, J. D. (2020), Inspection and classification of semiconductor wafer surface defects using CNN deep learning networks, Applied Sciences, 10(15), 5340.
[https://doi.org/10.3390/app10155340]

-
Choi, J. and Kim, S. B. (2024), Multi-Stage Process Diagnosis Networks in Semiconductor Manufacturing, IEEE Access.
[https://doi.org/10.1109/ACCESS.2024.3375367]

-
Deen, M. J. and Pascal, F. (2017), Electrical characterization of semiconductor materials and devices, Springer Handbook of Electronic and Photonic Materials, 1-1.
[https://doi.org/10.1007/978-3-319-48933-9_20]

-
Garcia, G. R., Michau, G., Ducoffe, M., Gupta, J. S., and Fink, O. (2022). Temporal signals to images: Monitoring the condition of industrial assets with deep learning image processing algorithms, Proceedings Of The Institution Of Mechanical Engineers, Part O: Journal of Risk and Reliability, 236(4), 617-627.
[https://doi.org/10.1177/1748006X21994446]

-
He, K., Chen, X., Xie, S., Li, Y., Dollár, P., and Girshick, R. (2022), Masked autoencoders are scalable vision learners, In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 16000-16009.
[https://doi.org/10.1109/CVPR52688.2022.01553]

-
Hosseinpour, F., Ahmed, I., Baraldi, P., Behzad, M., Zio, E., and Lewitschnig, H. (2022), An Unsupervised Method for Anomaly Detection in Multi-Stage Production Systems Based on LSTM Autoencoders, In Extended Abstracts, 1346-1352.
[https://doi.org/10.3850/978-981-18-5183-4_R22-19-604-cd]

-
Hwang, R., Park, S., Bin, Y., and Hwang, H. J. (2023), Anomaly Detection in Time Series Data and its Application to Semiconductor Manufacturing, IEEE Access, 11, 130483-130490.
[https://doi.org/10.1109/ACCESS.2023.3333247]

-
Kim, J., Mok, C., Kim, H., Kim, J., Ko, H., Hong, J., and Kim, S. B. (2024), Anomaly Classification and Key Segment Detection in Semiconductor Manufacturing Processes Using Image-Based Siamese Networks, Journal of the Korean Institute of Industrial Engineers, 50(4), 222-232.
[https://doi.org/10.7232/JKIIE.2024.50.4.222]

- Li, K. L., Huang, H. K., Tian, S. F., and Xu, W. (2003, November), Improving one-class SVM for anomaly detection, In Proceedings of the 2003 international conference on machine learning and cybernetics (IEEE Cat. No. 03EX693), IEEE, 5, 3077-3081.
-
Li, W., Qi, F., Tang, M., and Yu, Z. (2020), Bidirectional LSTM with self-attention mechanism and multi-channel features for sentiment classification, Neurocomputing, 387, 63-77.
[https://doi.org/10.1016/j.neucom.2020.01.006]

-
Michau, G., Hu, Y., Palmé, T., and Fink, O. (2020), Feature learning for fault detection in high-dimensional condition monitoring signals, Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 234(1), 104-115.
[https://doi.org/10.1177/1748006X19868335]

-
O’Leary, J., Sawlani, K., and Mesbah, A. (2020), Deep learning for classification of the chemical composition of particle defects on semiconductor wafers, IEEE Transactions on Semiconductor Manufacturing, 33(1), 72-85.
[https://doi.org/10.1109/TSM.2019.2963656]

-
Pang, G., Shen, C., Cao, L., and Hengel, A. V. D. (2021), Deep learning for anomaly detection: A review, ACM Computing Surveys (CSUR), 54(2), 1-38.
[https://doi.org/10.1145/3439950]

- Park, Y. and Lee, H. (2010), Development of Real-Time Fault Monitoring and Detection System for Next Generation Fab, Korea Academia-Industrial cooperation Society, 172-178.
-
Radoi, A. (2022), Multimodal satellite image time series analysis using GAN-based domain translation and matrix profile, Remote Sensing, 14(15), 3734.
[https://doi.org/10.3390/rs14153734]

-
Rahim, N., El-Sappagh, S., Ali, S., Muhammad, K., Del Ser, J., and Abuhmed, T. (2023), Prediction of Alzheimer's progression based on multimodal deep-learning-based fusion and visual explainability of time-series data, Information Fusion, 92, 363-388.
[https://doi.org/10.1016/j.inffus.2022.11.028]

-
Shin, C. K. and Park, S. C. (2000), A machine learning approach to yield management in semiconductor manufacturing, International Journal of Production Research, 38(17), 4261-4271.
[https://doi.org/10.1080/00207540050205073]

-
Shin, W., Kahng, H., and Kim, S. B. (2022), Mixup-based classification of mixed-type defect patterns in wafer bin maps, Computers & Industrial Engineering, 167, 107996.
[https://doi.org/10.1016/j.cie.2022.107996]

-
Susto, G. A., Beghi, A., and McLoone, S. (2017, May), Anomaly detection through on-line isolation forest: An application to plasma etching, In 2017 28th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC), IEEE, 89-94.
[https://doi.org/10.1109/ASMC.2017.7969205]

-
Susto, G. A., Terzi, M., and Beghi, A. (2017), Anomaly detection approaches for semiconductor manufacturing, Procedia Manufacturing, 11, 2018-2024.
[https://doi.org/10.1016/j.promfg.2017.07.353]

- Vaswani, A. (2017), Attention is all you need, arXiv preprint arXiv:1706.03762, .
-
Wang, M., Wang, W., Zhang, X., and Iu, H. H. C. (2022), A new fault diagnosis of rolling bearing based on Markov transition field and CNN, Entropy, 24(6), 751.
[https://doi.org/10.3390/e24060751]

- Wang, Z. and Oates, T. (2015), Imaging time-series to improve classification and imputation, arXiv preprint arXiv:1506.00327, .
-
Xia, X., Pan, X., Li, N., He, X., Ma, L., Zhang, X., and Ding, N. (2022), GAN-based anomaly detection: A review, Neurocomputing, 493, 497-535.
[https://doi.org/10.1016/j.neucom.2021.12.093]

- Xu, J., Wu, H., Wang, J., and Long, M. (2021), Anomaly transformer: Time series anomaly detection with association discrepancy, arXiv preprint arXiv:2110.02642, .
백민지 : 금오공과대학교 신소재공학부에서 2017년 학사학위를 취득하고 고려대학교 산업경영공학과에서 석사과정에 재학 중이다. 연구 분야는 머신러닝, 딥러닝을 적용한 이상 탐지와 제조 분야에 응용하는 연구를 수행하고 있다.
김성범 : 고려대학교 산업경영공학부 교수로 2009년부터 재직하고 있으며, 인공지능공학연구소 소장, 기업산학연협력센터 센터장, 한국데이터마이닝학회 회장을 역임했다. 미국 University of Texas at Arlington 산업공학과에서 교수를 역임하였으며, 한양대학교 산업공학과에서 학사학위를 미국 Georgia Institute of Technology에서 산업시스템공학 석사 및 박사학위를 취득하였다. 인공지능, 머신러닝, 최적화 방법론을 개발하고 이를 다양한 공학, 자연과학, 사회과학 분야에 응용하는 연구를 수행하고 있다.