머신러닝을 이용한 태양광 발전량 예측 모델 비교
© 2021 KIIE
Abstract
The amount of new renewable energy generation is increasing worldwide every year. Among many new renewable energy sources, solar energy generation using solar energy accounts for the highest proportion of new renewable energy generation. There is a variation in power production because solar power generation is more affected by climate conditions compared to power generation using crude oil or oil. In order to accurately predict solar energy generation dependent on climate variables, this study compares the performance of machine learning-based solar power generation prediction models using weather forecast data from the current forecast technology, Numeric Weather Prediction (NWP). In this study, we experimented on two NWP types, and 7 machine learning models depending on 21 photovoltaic(pv) power stations. Based on results, we select the model with the lowest statistical indicators nMAE(%) by region as the optimal model for the region. Finally, experimental results show that the 7-Block ANN model devised in this study is better than conventional machine learning models.
Keywords:
Photovoltaic Generation Forecasting, Predict of solar power generation, Deep Learning, Machine Learning1. 서 론
전 세계적으로 환경 오염과 자원 고갈의 문제가 이슈화되면서 대체 에너지 개발이 대두되고 있다. 많은 대체 에너지 중에서, 재사용이 가능한 신 재생 에너지에 관한 연구가 주목받고 있다. 이는 ‘비고갈성 에너지’라고 불리며 이를 이용한 발전량의 비중은 점차 커지고 있다. 대한민국 전력거래소의 ‘2019년 발전 설비 현황’에 따르면, 신 재생 에너지 발전 비중은 13%를 차지했고 이 중에서 태양광 에너지를 이용한 발전은 67%에 달했다. 정부는 2040년까지 신 재생 에너지 발전량을 30~35%로 높이겠다는 ‘에너지 기본 계획’을 확정했다. 이로써, 신 재생 에너지 발전의 대부분을 차지하는 태양광 에너지 발전은 중요한 연구 대상으로 자리 잡았다.
태양광 에너지를 발전함에 있어 태양광 발전량을 정확히 예측하는 것은 중요하다. 그 이유는 다음과 같다. 첫째, 발전량의 정확한 예측은 전력 가격을 결정하는 중요한 요인이 되기 때문에 적정 가격에 맞는 유동적이고 안정적인 발전 설계가 가능하다. 둘째, 태양광 발전 시스템의 가동 정도를 정할 수 있기 때문에 태양광 발전을 담당하는 사업자의 수익에도 영향을 준다. 이에 따라 국제에너지기구(IEA)는 개별 태양광 발전기의 예측발전량 확보를 권고했으며 해외 주요 국가에서는 이미 에너지 발전량 예측에 대한 제도를 시행 중이다. 2020년 9월, 우리나라 또한 관련 제도를 도입했으며 2021년 상반기부터 이 제도가 시행됐다. 이 제도는 재생 에너지 발전량을 하루 전에 미리 예측하여 제출하고 당일날 일정 오차율 이내일 경우 정산금(인센티브)을 지급하는 것이다. 이는 정부가 태양광 발전량 예측의 중요성을 인지하고 있다는 뜻이며, 발전량 사업에서 다양한 예측모델이 유용하게 사용될 것임을 시사한다.
고전의 태양광 발전량 예측 연구에서는 단일 값들을 이용하여 예측하는 Autoregressive model(AR model), Moving Average model(MA model), 그리고 이 둘을 결합한 ARIMA 등의 고전적인 시계열 모델을 사용하였지만, 최근 선행연구에서는 다중 값들을 Input으로 사용하여 예측하는 머신러닝 기반의 모델을 많이 사용한다. 이런 머신러닝 모델 성능이 고전적인 시계열 모델의 성능보다 높았던 사례가 많았기 때문에, 본 연구에서는 선행 연구에서 사용했던 모델들 중 다양한 머신 러닝 기반 모델의 성능을 비교한다. 최종적으로 국내 발전소의 태양광 발전량을 정확하게 예측하도록 돕는다. 우리나라 총 21곳의 발전소를 대상으로 하였고 각 지역에서 NWP를 통해 예보된 기상 데이터와 발전량 데이터를 활용하여 연구를 진행했다. NWP 모델과 지역에 따라 모델을 구축했고 태양광 발전 분야에서 많이 사용되고 있는 통계 지표를 기반으로 한 평가지표인 nominal Mean Absolute Error(nMAE)로 평가하였다.
본 연구의 구성은 다음과 같다. 2장에서는 과거 태양광 발전량 예측에 대한 연구를 다루고 3장에서는 본 연구에서 사용한 전처리 방법과 평가지표를 소개한다. 4장에서는 사용한 방법론에 대하여 설명하고 5장에서는 구축된 모델의 성능을 비교 및 결과를 분석한다. 마지막으로 6장에서는 본 연구의 결론 및 향후 한계점을 언급한다.
2. 선행 연구
과거의 태양광 발전량 예측 연구에는 단일 태양광 발전량 값만을 사용하여 예측하는 연구가 있었다. Radial Basis Function Networks(RBF Networks)를 발전량 예측에 사용한 연구(Mellit et al., 2005)는 RBF모델과 B.P 알고리즘을 이용하여 Mean Relative Error(MRE)를 측정했다. ARMA를 개조하여 Mean Absolute Error(MAE)를 낮춘 연구(Cheng et al., 2012)는 시계열 통계모형인 ARMA를 개조한 Least Square ARMA(LS-ARMA)로 예측 오차율을 낮췄고 Artificial Neural Network(ANN)의 모델링을 제안하였다.
다음으로 온도나 구름과 같은 외부 기후 변수들이 태양광 발전량에 영향을 준다는 연구가 있었다. 태양광 발전판 모듈의 온도와 태양광 발전량의 의존성을 다룬 연구(Skoplaki and Palyvos, 2009)는 태양광 발전판 모듈의 온도가 태양광 발전량의 출력에 선형적으로 좌우된다는 결과를 냈고 구름 조건을 이용하여 발전량을 예측하는 연구(Nelson et al., 2009)에서는 구름이 존재할 때, 일반적인 모델은 발전량을 과대 예측하는 것을 확인하였다. 습도와 태양광 발전판 셀의 성능을 비교한 연구(Mekhilef et al., 2012)에서는 상대습도가 증가함에 따라 태양광 발전판 셀에 입사하는 태양광 양이 줄어듦을 밝혔다.
최근에는 기후 정보를 독립변수로 사용하는 다양한 머신러닝 모델로 발전량을 예측하는 연구가 활발히 진행되고 있다. ARIMA, K-Nearest Neighbor(KNN), ANN, Genetic Algorithms ANN의 성능을 비교한 연구(Pedro and Coimbra, 2012)는 기본 통계모형인 ARIMA 모형보다 머신러닝 모델의 성능이 좋다는 것을 보였고 Multiple Linear Regression(MLR), Feed-Forward Neural Network(FFNN), Generalized Regression Neural Network(GRNN)를 비교한 연구(Ramsami and Oree, 2015), MLR, Random Forest(RF), Multi Layer Perceptron Artificial Neural Network(MLP-ANN)의 성능을 비교한 연구(Kayri et al., 2017), 그리고 RF, Extremely randomised regression Trees(ET), Support Vector Regression(SVR)의 성능을 비교한 연구(Ahmad et al., 2018) 등에서는 태양광 발전량 예측 분야에서 여러 머신러닝 모델의 성능을 비교하는 내용을 다루었다.
국내에서도 기상정보를 활용한 머신러닝 기반의 태양광 발전량 예측 연구가 진행되었다. 기상자료를 이용한 기계학습모델 기반 태양광 발전량 예측(Seo et al., 2017), Recurrent Neural Network-Long Short-Term Memory(RNN-LSTM)를 이용한 태양광 발전량 단기 예측 모델(Shin and Kim, 2018), 기상 예보를 이용한 머신러닝 알고리즘 기반 태양광 발전량 예측 기법(Kim, 2019), 그리고 기상 예보를 활용한 LSTM 기반 24시간 태양광 발전량 예측모델(Son et al., 2020) 등의 연구는 기상 정보를 활용하여 여러 가지 머신러닝 모델로 발전량을 예측하였다.
앞선 국내 연구는 최대 24시간을 예측하는 것과 적은 개수의 모델들을 비교하는 데에 그쳤지만, 본 연구는 기상 예보 정보를 활용하여 최대 48시간 뒤까지 태양광 발전량 예측을 수행하였다. 또한 본 연구에서는 국내의 다양한 발전소의 발전량을 높은 성능으로 예측하는 7-Block ANN 모델을 제안한다.
3. 데이터 전처리 및 평가 지표
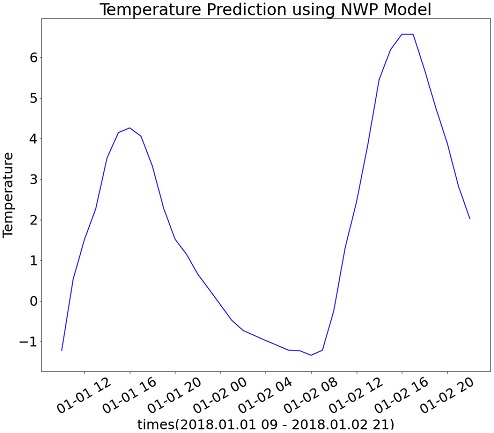
본 연구의 데이터는 한국에너지기술연구원에서 제공받은 데이터이며, 2018년의 데이터를 Train Set로, 2019년의 데이터를 Test Set으로 사용했다. 본 연구의 데이터는 Numeric Weather Prediction(NWP) 기상예보 데이터와 각 발전소의 태양광 발전량 데이터로 구성되었다. NWP란 대기 현상의 역학을 컴퓨터를 활용하여 연속적으로 수치 적분함으로써 미래의 날씨 및 대기 상태를 정량적으로 예측하는 과정이다. NWP는 다양한 상태의 날씨들을 물리적으로 모사하기 때문에, 최근에는 이 기상 예보 데이터를 함께 사용하여 태양광 발전량을 예측한다. <Figure 1>은 본 연구에서 사용한 NWP 모델의 기상 변수 중 온도 변수를 나타낸다. 기준시각(2018년 1월 1일 9시)부터 36시간 뒤까지 NWP 모델(UML_09_KST)을 사용하여 기온을 예측한 그래프를 나타낸다.
Train Set의 NWP 예보 데이터는 최대 36시간 뒤까지의 예보 데이터가 존재했으나, Test Set의 NWP 예보 데이터는 최대 48시간 뒤까지 예보 데이터가 존재했다. 이 경우, 학습 데이터에 없는 Sequence의 샘플에 대해서도 예측을 수행했다.
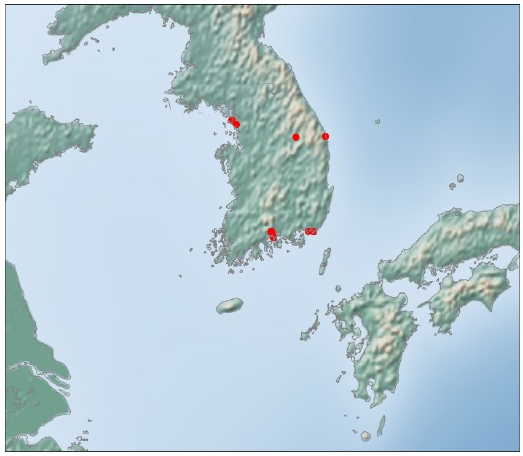
지역별 발전소는 부산 5곳, 삼척 3곳, 인천 3곳, 영월 1곳, 하동 10곳이 존재했고 발전소별로 모델을 구축 후, 지역별로 성능을 비교하였다. <Figure 2>는 각 발전소에 해당하는 위도와 경도를 한반도 위에 표시한 그림이다. 각 지역의 발전소는 서로 밀집되어 있는 것을 확인할 수 있다.
3.1 학습 데이터 전처리 및 테스트 데이터의 평가
NWP 모델의 기상 정보 데이터는 예보 시작 시간을 기준으로 한 시간 마다 36시간 뒤까지 기상을 예측한 값이고 태양천정각, 태양방위각, 수평면 전일사량, 법선면 직달일사량, 기온, 지표 온도, 해면 기압, 풍속, 상대습도, 운량, 시간당 강수량을 포함한다. 기상 데이터와 발전량 데이터는 모두 2018년 1월 1일부터 2019년 12월 31일까지 1시간 단위로 기록되어 있다. NWP 모델 데이터와 발전량 데이터는 기록 시간의 차이가 존재했다. 2019년 1월 1일 0시의 발전량 데이터는 2019년 1월 1일 0시부터 1시까지의 누적 발전량을 의미하는 반면에, NWP 모델의 2019년 1월 1일 0시의 데이터들은 2018년 12월 31일 23시부터 2019년 1월 1일 0시까지의 값들을 의미했다. 이를 보정하기 위하여 NWP 모델의 기록 시각에 한 시간 만큼을 빼주었다.
구름 운량(하층 운량, 중층 운량, 상층 운량)의 세 개의 변수에 대해서는 정상 범위(0에서 1 사이의 값)를 벗어난 -999를 갖는 이상치에 대해서 0(구름 없음)으로 대체하였고, 매우 낮은 음수 값을 가질 수 없는 지표 온도 변수값 중 -1272.15인 지표 온도를 한 시간 뒤의 지표 온도로 대체하였다. 또한, 0보다 작을 수 없는 해면 기압 변수값중 -9.99인 해면 기압을 한 시간 뒤의 해면 기압으로 대체하였다. 한편, 법선면 직달일사량 변수에 대해서는 다른 변수보다 많은 샘플이 이상값이었다. 법선면 직달일사량 값은 대기권 밖의 일사량을 뜻하는 태양상수의 값을 넘을 수 없다. 그렇기 때문에, 머신러닝과 인공신경망 모델의 경우는 해당 변수의 값이 태양 상수인 1367을 초과하거나 음수인 해당 샘플을 삭제하였다. 그러나, 순환신경망 모델의 경우는 샘플을 삭제했을 때, 학습에 들어가는 샘플이 일정한 Sequence 간격으로 유지되지 않는다. 따라서 이 경우는 이상값을 한 시간 전과 한 시간 후의 법선면 직달일사량 값을 평균하여 대체하였다. 또한, 순환신경망 모델에 대해서는 37개의 시퀀스가 채워지지 않는 Subset들을 제거하고 학습하였다.
본 연구의 발전량 데이터는 30%~40%가 0이었고, 대부분은 밤 시각이었다. 태양광 발전기는 밤 시간대에 작동하지 않기 때문에, 본 연구에서는 낮 시간의 발전량에 집중했다. 따라서, 시계열 시퀀스를 고려하지 않는 머신러닝과 인공신경망 모델에 대해서는 태양 천정각의 코사인값이 Cos75° 이상인 샘플을 제거하고 학습했으며, 모델을 평가할 때에도 해가 떠 있지 않은 시간을 제외하였다. 해가 떠 있지 않은 시간은 코사인 태양 천정각이 Cos75° 이상일 때로 계산하였다.
3.2 평가지표
MAE는 실제값과 예측값의 오차에 절대값과 평균을 차례로 취해준 값이며 식 (1)과 같이 구할 수 있다. 이때, yi는 실제값을, 는 예측값을 나타내며 n은 샘플의 개수를 나타낸다.
| (1) |
이 지표는 실제값과 예측값의 오차가 어느 정도인지 판단할 수 있는 지표이다.
RMSE는 실제값과 예측값의 오차에 제곱, 평균 그리고 제곱근을 차례로 취해준 값이며 식 (2)와 같이 구할 수 있다.
| (2) |
이 지표는 MAE와 마찬가지로 실제값과 예측값의 오차가 어느 정도인지 판단할 수 있다.
MBE는 실제값과 예측값의 단순 오차에 평균을 취해준 값이며 식 (3)과 같이 구할 수 있다.
| (3) |
이 지표는 예측값들이 평균적으로 실제값보다 작게 예측되었는지 혹은 크게 예측되어있는지를 판단할 수 있는 지표이다.
본 연구에서는 각 발전소의 최대 발전량이 모두 달랐기 때문에 지역 간에 오차의 크기가 달랐다. 오차를 같은 단위로 비교하기 위하여, 위의 세 가지 지표를 Capacity(각 발전소의 최대 발전량)로 나눈 nominal Mean Absolute Error(nMAE), nominal Root Mean Square Error(nRMSE) 그리고 nominal Mean Bias Error(nMBE)의 지표를 사용했으며, 수치 비교의 편의를 위하여 nMAE, nRMSE, nMBE에 100을 곱한 nMAE(%), nRMSE(%), nMBE(%)를 사용했다. <Table 1>은 각 지역 발전소의 Code 명과 그에 해당하는 최대발전량을 나타낸 표이다.
태양광 발전량 예측 분야에서 대부분의 선행연구는 평가 지표로 MAE를 사용했다. 따라서 본 연구의 평가 지표는 MAE 기반인 nMAE(%)를 사용했다.
4. 태양광 발전량 예측 모델
4.1 K-Nearest Neighbor (KNN) 모델
KNN 모델은 정의한 거리를 기반으로 예측할 Instance와 가장 가까운 K개의 이웃들의 목표값을 평균 내어 예측값으로 사용한다. 본 연구에서는 유클리디안 거리(Euclidean Distance)를 기준으로 Instances 간의 거리를 측정하였다. 두 Instances의 거리는 식 (4)와 같이 구할 수 있다.
| (4) |
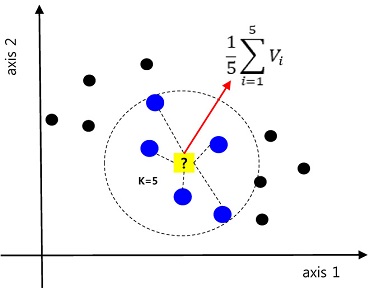
여기서 (x1, x2, ⋯, xp), (y1, y2, ⋯, yp)는 p차원의 서로 다른 Instance를 의미한다. <Figure 3>은 하나의 Test Instance에 대하여 K=5일 때, 예측값을 도출하는 과정이다. 이때, Vi는 예측하고자 하는 샘플과 가장 가까운 5개 샘플의 목표값을 의미한다.
4.2 Support Vector Machine(SVM) 모델
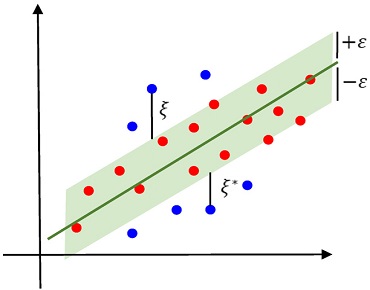
SVM 모델 중에서 회귀 역할을 수행하는 Support Vector Regression(SVR) 모델은 실제값과 예측값의 오차는 작게 하되, 일정 범위 내에서의 오차를 용인한다. <Figure 4>에서 ϵ은 허용하는 잡음 정도를 나타내고 ξ는 허용하는 잡음을 벗어난 정도를 나타낸다.
<Figure 3>의 회귀 직선을 추정하기 위하여, 식(5)의 목적 식을 최소화하는 최적의 파라미터(w, b)를 찾는다. 이때, 추정한 w와 b는 회귀 직선의 모수가 된다. 이 식은 라그랑지안 쌍대문제와 KKT조건을 이용하여 최적해를 구할 수 있다. 이 식에서 하이퍼파라미터 C는 일정 error의 밖에 위치한 점들에 대한 Penalty의 가중치를 뜻한다. 이는 과적합을 방지하는 역할을 하고 회귀선의 평탄도와 편차가 결정된다.
| (5) |
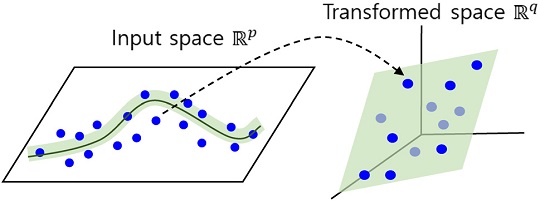
SVM 모델은 일반적으로 선형성을 가진 데이터에 적합하며, 비선형성을 가진 데이터는 Kernel function을 사용하여 선형성을 만족하도록 고차원 공간으로 사상한 뒤, 식 (2)의 목적 식을 최소화한다. 본 연구에서는 가우시안 분포를 기반으로 한 RBF Kernel을 사용하였다. <Figure 5>는 p차원의 공간상의 값들이 Kernel에 의해 q차원으로 매핑되는 과정이다. 이때, p < q이다.
4.3 Random Forest (RF) 모델
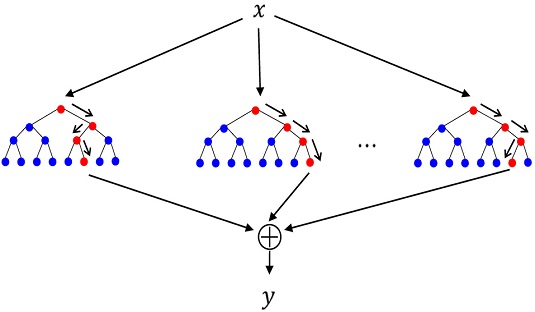
RF Regression 모델은 Bagging 기법을 사용하여 각 트리마다 랜덤하게 데이터를 샘플링한 뒤, 무작위로 Feature를 정하고 Decision Tree를 구성한다. 그리고 모든 Decision Trees의 평균으로 예측값을 구한다. <Figure 6>는 x 값이 input으로 들어왔을 때, output 값 y를 산출하는 그림을 나타낸다. 각 회귀 Tree의 output을 평균하여 종합적으로 모으는 앙상블 기법으로 모델이 과적합 될 확률을 줄인다.
4.4 XG boost (XGB) 모델
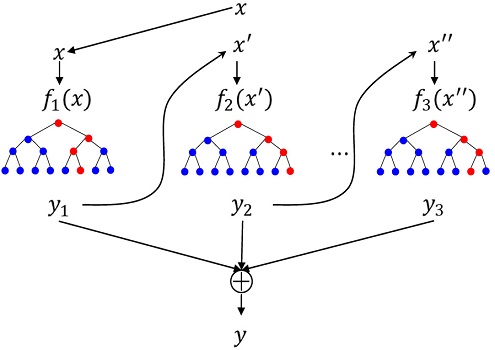
Gradient Boost (GB) 모델은 연속적인 weak model들을 구축한 뒤, residual을 줄이는 방향으로 결합하여 object function의 loss를 줄여나가는 모델이다. <Figure 7>과 같이, 원래의 데이터 x를 학습한 weak Model f1(x)를 통해 residual xʹ를 구하고 xʹ를 학습한 f2(x)를 통해 xʹʹ를 구한다. 이러한 과정들을 조건이 만족할 때까지 반복한 후, 모든 식을 합하여 예측한다.
XGB 모델은 위의 GB 모델의 단점을 보완한 모델이다. GB의 weak model들이 train data의 residual을 계속해서 줄이는 과정에서 Overfitting이 쉽게 되는 문제점을 Regularization term을 추가해 이를 해결한 알고리즘이다. XGB 모델의 loss function은 식 (6)과 같다.
| (6) |
여기서 T는 tree의 최종 node의 개수, w는 최종 node의 score로 loss function에 의해 학습되는 값이다.
4.5 7-Block Artificial Neural Network (7-Block ANN) 모델
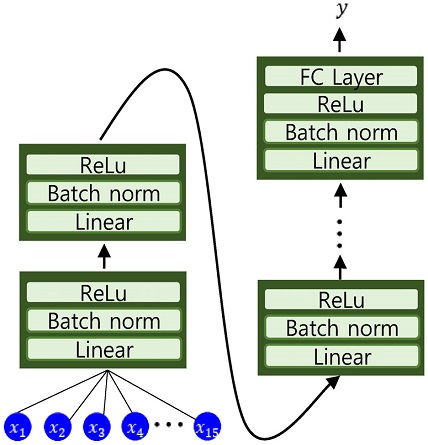
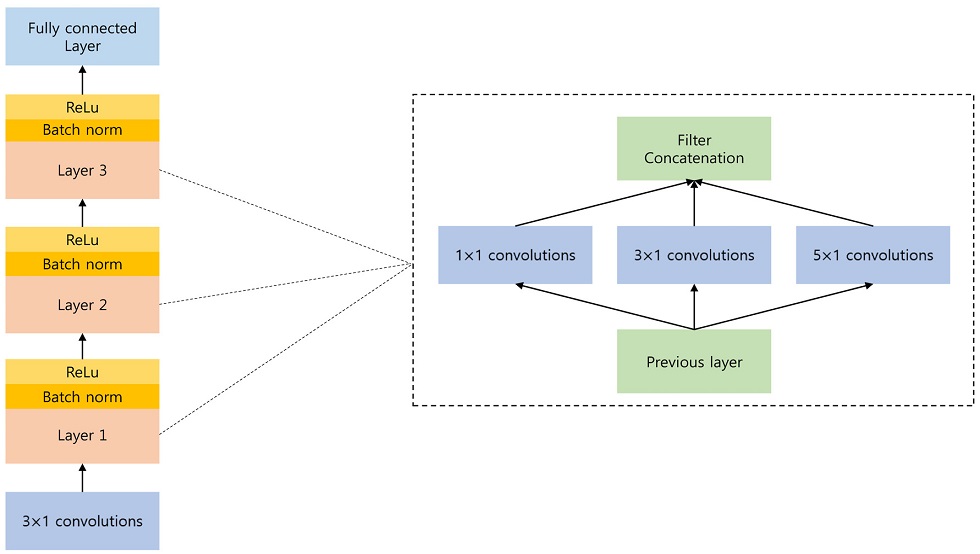
ANN 모델은 하나 이상의 Perceptron이 여러 개의 층을 이룸으로써 고차원의 데이터를 표현하는 방향으로 학습하여 예측을 수행한다. 입력층에서 출력층으로 선형 변환과 비선형 변환을 거치며, 정의한 로스에 따라 실제값과 근접하게 가중치를 업데이트하는 방식으로 학습이 진행된다. <Figure 8>은 본 연구에서 제안한 7-Block ANN 구조를 도식화하여 나타냈다. Input 값을 받는 Block을 포함한 6개의 Block과 1개의 Output Block에서는 각각 차례로 Linear, Batch norm, ReLu Layer를 포함하며, Output Block은 Fully Connected Layer를 추가로 포함한다.
본 연구에서 ANN의 구조를 <Figure 8>과 같이 구성한 이유는 다음과 같다. 먼저 Linear Layer에서는 NWP 모델로 예측한 기상변수를 Input으로 받는 역할을 담당한다. 이때, Linear Layer에서 나온 Output 값들은 이전 Layer의 파라미터 변화로 인해 기후 변수들의 분포가 바뀌는 Covariate Shift 문제가 나타난다. 따라서 이후에 Batch Normalization Layer를 사용한다. Batch Normalization Layer는 신경망 자체에서 평균과 분산을 조정하기 때문에 Covariate Shift 문제를 해결할 수 있다. 마지막으로 활성화 함수를 쓰는 이유는 다음과 같다. 딥러닝의 층을 깊이 쌓았을 때, 비선형 함수를 사용하지 않는다면, 층을 깊게 하는 의미가 없어진다. 따라서 비선형 함수인 활성화 함수를 사용한다. 특히, 본 연구에서는 ReLu 함수를 활성화 함수로 사용하였다. ReLu 함수는 출력과 멀리 있는 Layer까지 Gradient가 전달되며, 다른 활성화 함수보다 계산 복잡도가 낮다는 장점이 있다. 따라서 딥러닝이 학습되는 속도가 빠르며, Gradient가 소실되는 문제인 Gradient Vanishing 문제가 적게 일어난다.
따라서 이 세 가지의 Layer를 사용하여 하나의 블록을 형성했고 실험적으로 총 7개의 Block을 이어붙인 7-Block ANN을 본 연구의 모델로 정했다.
4.6 Convolution Neural Network (CNN) 모델
CNN 모델은 이미지 데이터를 처리하는 데에 많이 사용되지만, 1D-Convolution을 이용한 태양광발전량을 예측한 연구(Huang and Kuo, 2019)에서는 이미지뿐만 아니라 시계열 예측 문제에서도 좋은 성능을 낼 수 있음을 밝혔다. 본 연구에서는 각 Layer에 Google Net(Szegedy et al., 2015)의 Inception Module의 구조를 변형하여 사용하였다. <Figure 9>는 본 연구에서 사용한 CNN 모델의 구조와 내부의 Inception Module 그림이다.
4.7 Sequence to Sequence (S2S) 모델
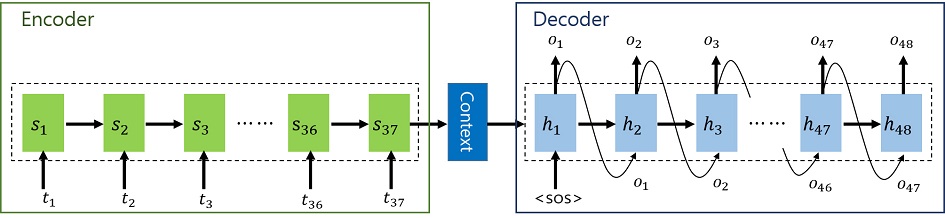
Input 문장을 받아 output 문 생성하는 연구(Sutskever et al., 2014)에서는 하나의 문장을 생성할 때, 단어를 연속적으로 생성하여 이어 붙이는 것보다 문장 자체를 생성하는 것이 더 좋은 성능을 갖는다는 것을 보였다. 요즘에는 Text 문제뿐만 아니라, 시계열 문제에서도 많이 사용되는 딥러닝 기반의 생성 모델이다. 이 모델은 Encoder와 Decoder Block으로 구성되어 있다. Encoder에서는 시계열 순으로 들어오는 정보를 축약하여 Decoder에 보내주는 역할을 하고 Decoder에서는 Encoder에서 받은 축약 정보를 바탕으로 시계열 데이터를 생성하는 역할을 담당한다. 본 연구에서는 S2S 모델의 Encoder, Decoder Cell로 LSTM과 GRU를 사용하였으며 <Figure 10>은 S2S 모델의 구조를 나타낸다.
5. 하이퍼파라미터 탐색 및 실험 결과
5.1 하이퍼파라미터 탐색
인공신경망과 순환신경망을 제외한 머신러닝 모델은 파이썬의 scikit-learn 패키지를 이용하여 구현하였으며, 인공신경망과 순환신경망 모델은 pytorch 패키지를 사용했다. 머신러닝 모델은 Default 하이퍼파라미터를 기준으로 다음과 같은 범위에서 Grid Search 방법을 통해 탐색하였다. KNN 모델은 이웃 샘플 수(n_neighbors)를 5부터 20 사이의 범위에서 5씩 증가시키며 실험하였다. RF 모델은 Feature의 수를 고르는 방법(max_features)이 [auto, sqrt]인 두 가지, 생성할 Tree 개수(n_estimators)가 [70, 100, 150]인 세 가지에 대하여 실험하였다. SVM 모델은 Smooth Decision Boundary Factor(C)가 [0.1, 1, 10, 100]인 네 가지, Training Point Reaches Factor(Gamma)가 [scale, auto]인 두 가지, 그리고 Kernel Function이 [rbf, sigmoid]인 두 가지 경우에 대해서 실험하였다. XGB 모델은 Learning Rate가 [0.03, 0.05, 0.07]인 세 가지, 가중치에 대한 L1 정규화 항(reg_alpha)이 [1e-5, 0.01, 0.1, 1, 100]인 다섯 가지, 그리고 가중치에 대한 L2 정규화 항(reg_lambda)이 [1e-5, 0.01, 0.1, 1, 100]인 다섯 가지에 대하여 실험하였다. 인공신경망과 순환신경망 모델은 200 Epochs를 넘어갔을 때의 성능향상이 뚜렷하지 않았기 때문에 200 Epochs로 고정하여 실험했고 L1 Loss를 사용하여 Gradient Descent 방법으로 최적의 가중치를 구했다. ReduceLROnPlateau Scheduler를 사용하여 인공신경망은 40 Patience마다, 순환신경망은 30 Patience마다 Learning Rate를 0.2배만큼 줄여가며 학습했다. 또, 은닉 노드의 수(hidden size)는 인공신경망은 [[32, 16, 8, 8, 4, 4, 2], [64, 32, 16, 16, 8, 8, 4], [256, 128, 64, 64, 32, 32, 16]]인 세 가지 경우에 대해서, 순환신경망은 [[1024, 512], [512, 256], [256, 128]]인 세 가지 경우에 대해서 실험했다. Optimizer 방법으로 인공신경망 모델은 AdamW를 사용했고 순환신경망 모델은 Adam을 사용하였다. NWP 모델에 따른 지역별 최고의 성능을 가진 모델의 하이퍼파라미터는 NWP 모델별로 각각 <Table 2>와 <Table 3>에 표기하였다.
5.2 실험 결과
각 발전소의 모델 성능을 NWP 모델의 예측 시작 시각별, 지역별에 따라 표로 나타냈으며, 지역별로 가장 우수한 모델에 대해서는 시간대별 평균 오차와 발전소별 평균 오차를 시각화하여 나타냈다. 본 연구의 평가 지표는 선행연구에서 흔히 쓰이는 MAE 기반인 nMAE(%)를 사용했으며, nMAE를 기준으로 가장 우수한 모델에 대해서는 nRMSE와 nMBE의 발전소별 그래프를 살펴보았다. 이때, nMBE는 오차를 평균할 때, 부호를 없애주는 과정이 없어서 예측값이 대체로 과대예측을 하였는지 혹은 과소예측을 하였는지 보여줄 수 있다. 평가 지표의 결과는 소수점 5자리에서 반올림하였다.
NWP 모델이 UML_03_KST인 경우의 결과는 <Table 4>와 같으며, 각 지역마다 nMAE가 가장 낮은 모델의 성능에 진한색으로 표시하였다. 부산, 영월 지역을 제외한 삼척, 인천, 그리고 하동 지역은 본 연구에서 제안한 7-Block ANN 모델 성능이 가장 우수했다. 또한 각 모델별로 오차를 평균하여 모델의 전반적인 성능을 비교했을 때에도 본 논문에서 제안한 7-Block ANN 모델의 성능이 가장 우수했다. 그다음으로 RF 모델, XGB 모델, KNN 모델, SVR 모델, GRU 모델, LSTM 모델, CNN 모델 차례 순으로 성능이 좋았다.
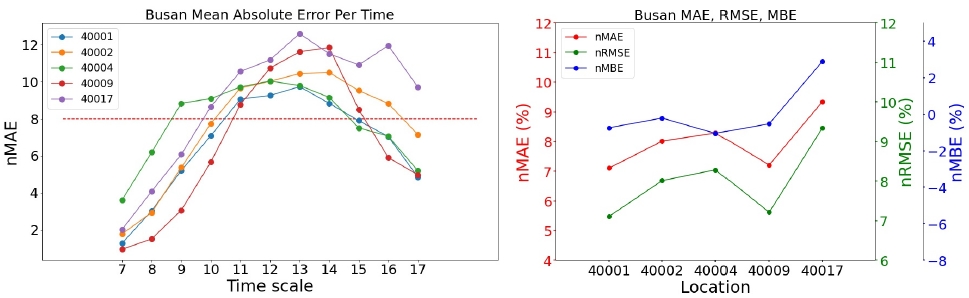
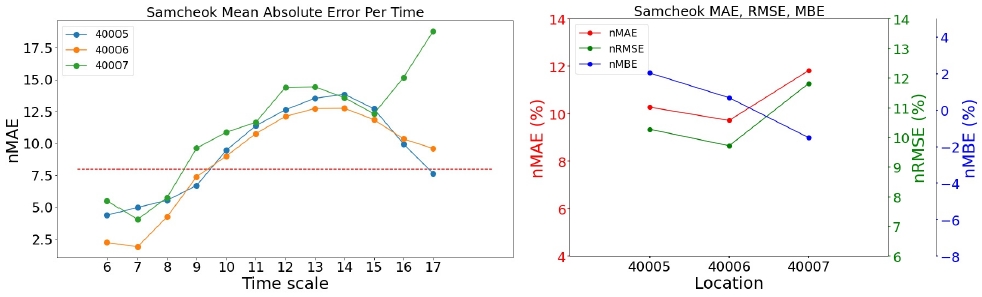
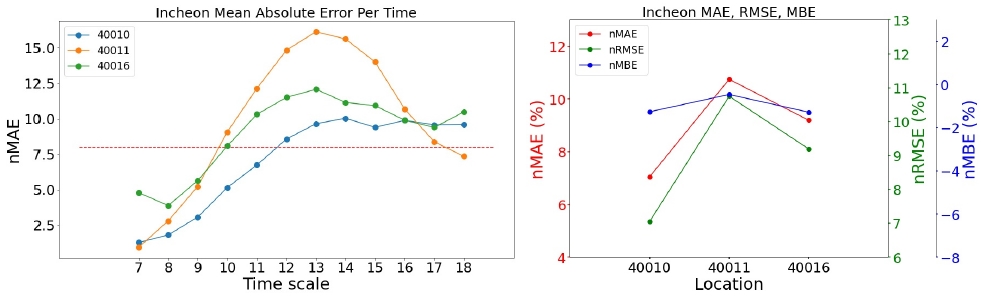
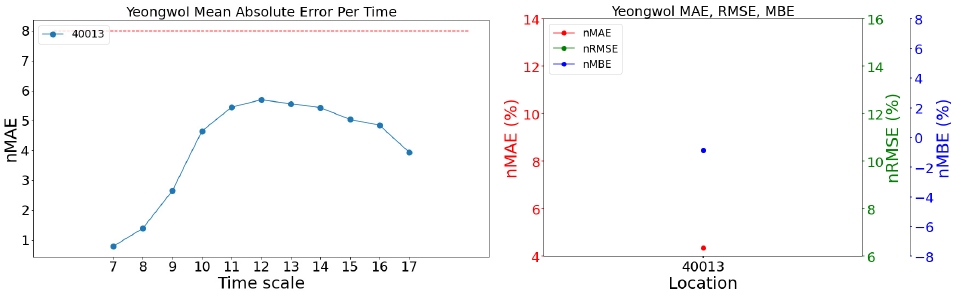
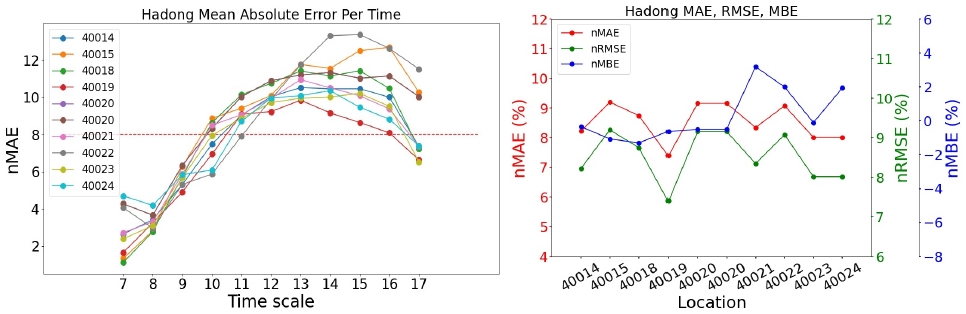
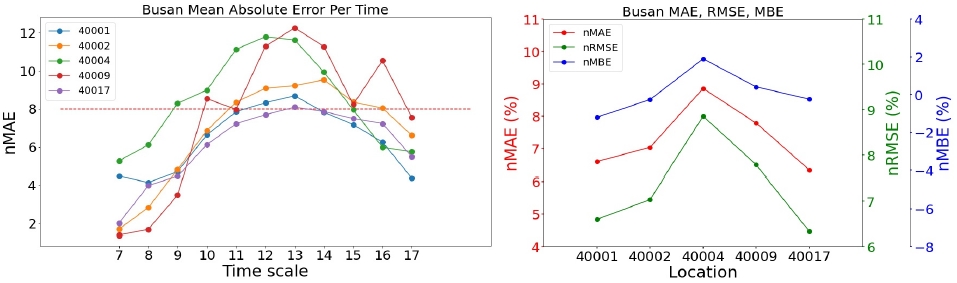
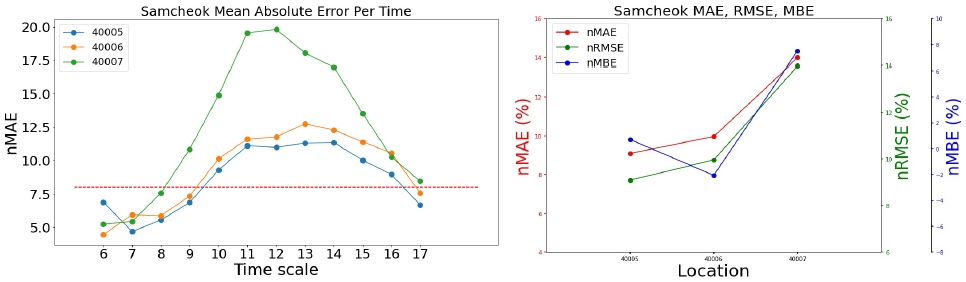
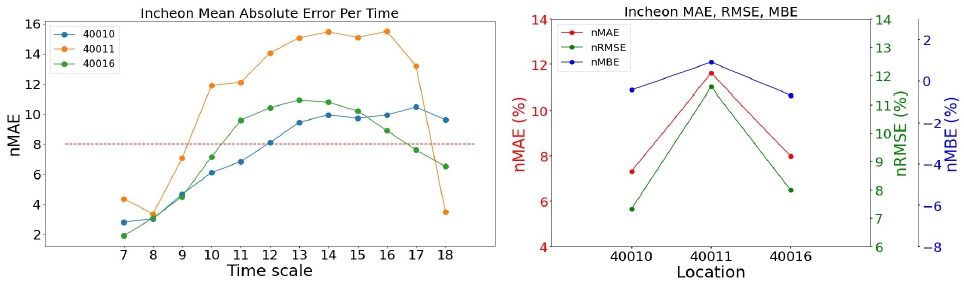
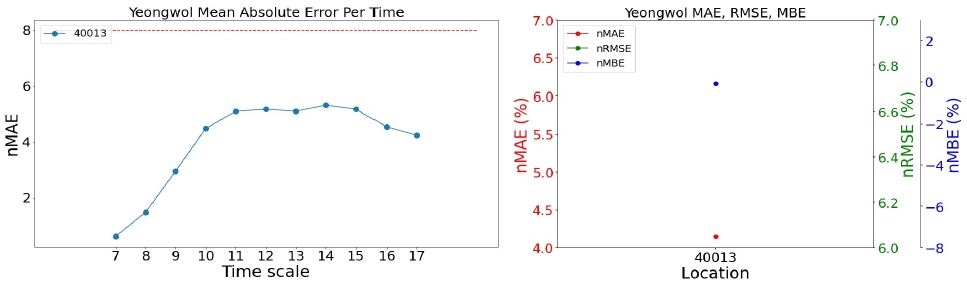
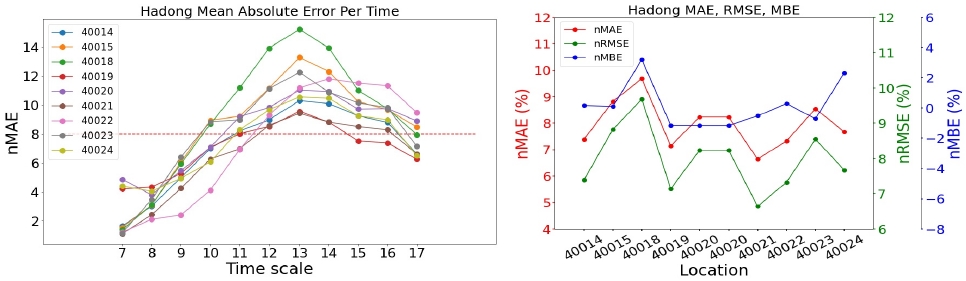
<Figure 11> ~ <Figure 15>와 <Figure 16> ~ <Figure 20>의 우측 그래프는 발전소별로 가장 우수한 모델의 세 가지의 성능 지표(nMAE, nRMSE, nMBE)를 나타낸 그래프이다. 모든 지역의 발전소에 대해서 nMAE와 nRMSE의 패턴은 매우 유사하여, 순위가 바뀌는 등의 결과는 발생하지 않는 것을 볼 수 있다. 이는 오차의 평균을 구하는 과정에 있어 nMAE는 오차의 절대값으로, nRMSE는 오차의 제곱으로 처리한다는 방법만 다르기 때문이다.
<Figure 11> ~ <Figure 15>의 좌측 그래프는 각 지역에서 가장 우수한 모델의 시간대별, 발전소별 평균 오차를 그린 그래프이다. 모든 모델에 대하여 아침과 초저녁 시간에는 모델의 예측이 잘 이루어졌지만, 한낮의 예측값에 대해 오차가 커지는 것을 확인할 수 있다. <Figure 12>에서 40005 발전소(삼척 소내; 삼척 1단계)의 nMBE는 약 2 정도로 예측값이 실제값보다 평균적으로 과대예측하고 있다고 해석할 수 있는 반면에, 40007 발전소(삼척 소내; 삼척 3단계)의 nMBE는 약 -2 정도로 예측값이 실제값보다 평균적으로 과소예측하고 있다. 이 두 발전소와 다르게, 40006 발전소(삼척 소내; 삼척 2단계)는 nMBE가 0에 가깝지만 nMAE와 nMBE가 각각 약 10을 나타내기 때문에 과대예측과 과소예측이 모두 일어나고 있음을 시사한다.
NWP 모델이 UML_09_KST인 경우의 결과는 <Table 5>와 같으며, 각 지역마다 nMAE가 가장 낮은 모델의 성능에 진한색으로 표시했다. UML_09_KST인 경우, 삼척 지역을 제외한 부산, 인천, 영월 하동 지역은 본 연구에서 제안한 7-Block ANN 모델의 성능이 가장 우수했고, ¡각 모델별로 오차를 평균하여 전반적인 성능을 비교했을 때에도 7-Block ANN 모델의 성능이 가장 좋았다. 그다음으로 KNN 모델, XGB 모델, SVR 모델, RF 모델, GRU 모델, LSTM 모델, 그리고 CNN 모델 차례 순으로 성능이 좋았다.
<Figure 16> ~ <Figure 20>의 좌측 그래프는 NWP 모델이 UML_09_KST인 경우의 각 시간대별, 발전소별 평균 오차이고 우측 그래프는 발전소별 성능 지표(nMAE, nRMSE, nMBE)를 나타낸 그래프이다. UML_03_KST의 결과와 같이 UML_09_KST에서도 모든 지역의 발전소에 대해서 nMAE와 nRMSE의 패턴은 유사한 것을 알 수 있다. 특히, <Figure 17>의 40007 발전소(삼척 소내; 삼척 3단계)의 nMBE는 약 7.5 정도로 예측값이 실제값보다 평균적으로 과대예측하고 있다.
NWP 모델이 UML_03_KST인 경우, 본 연구에서 제안한 7-Block ANN 모델이 5개중 3개의 지역에서 최고의 성능을 보였고, NWP 모델이 UML_09_KST인 경우에는 5개 중 4개의 지역에서 최고의 성능을 보였다. 한편, UML_03_KST이고 부산 지역일 때는 XGB 모델이, 영월 지역일 때는 RF 모델이 가장 좋은 성능을 보였고, UML_09_KST이고 삼척지역일 때는 SVR 모델이 가장 좋은 성능을 보였다.
본 연구에서 제안한 7-Block ANN 모델이 위의 세 경우에 대해서도 잘 예측함을 보이기 위해 다음과 같은 과정을 실시한다. 먼저 7-Block ANN 모델이 실제 발전량 값의 분포를 유사하게 따라가는지 살펴보기 위해, 모델의 예측값과 실제값의 차이를 시각적으로 살펴본다. 또한, 이를 수치적, 통계적으로도 유의미한 결과를 가져오는지를 검증하기 위해 정규성 검정 및 비모수 검정을 한다. 정규성 검정은 샘플 수가 2000개 이상일 때 사용되는 Kolmogorov-Smirnov Test를, 비모수 검정은 집단 간의 차이를 중위수를 이용하여 검정하는 Wilcoxon Rank Sum Test를 한다. 정규성 검정과 Wilcoxon Rank Sum Test의 유의수준은 모두 0.05로 설정하여 검정하였고 Kolmogorov-Smirnov Test와 Wilcoxon Rank Sum Test의 귀무가설 및 대립가설은 <Table 6>에 나타냈다. Kolmogorov-Smirnov Test의 K는 [UML_03_KST인 부산 지역의 실제값, UML_03_KST인 부산 지역의 XGB 모델 예측값, UML_03_KST인 영월 지역의 실제값, UML_03_KST인 영월 지역의 RF 모델 예측값, UML_09_KST인 삼척 지역의 실제값, UML_09_KST인 삼척 지역의 SVR 모델 예측값]인 총 6개의 집단을 각각 검정했으며, Wilcoxon Rank Sum Test는 해당 NWP 모델과 지역에 따른 세 경우의 실제값 집단과 예측값 집단을 검정했다. 이때, MedianGT는 실제값의 중위수를 나타내고 Medianprediction은 7-Block ANN 모델 예측값의 중위수를 나타낸다.
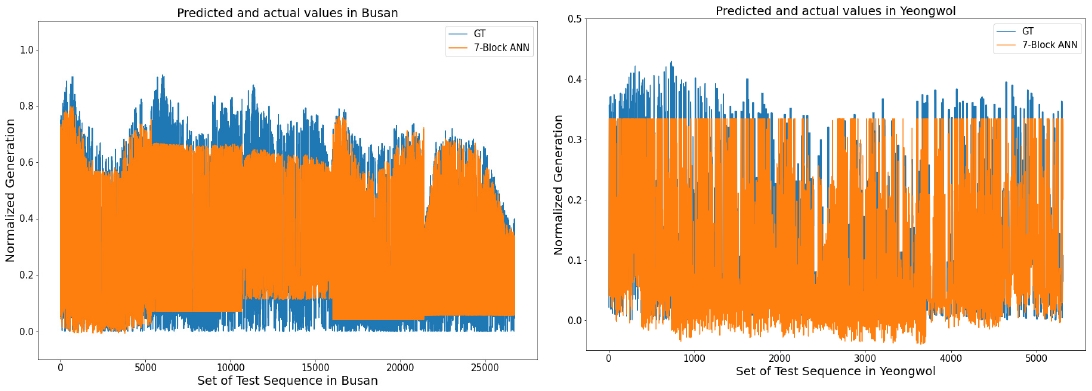
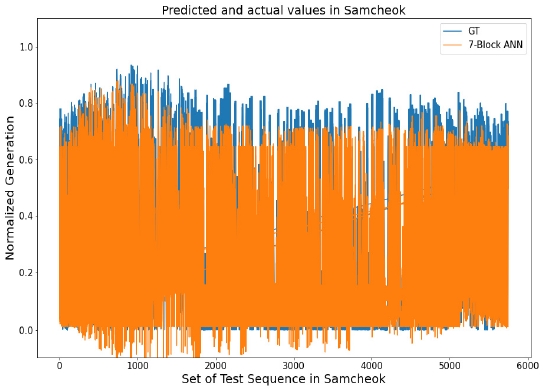
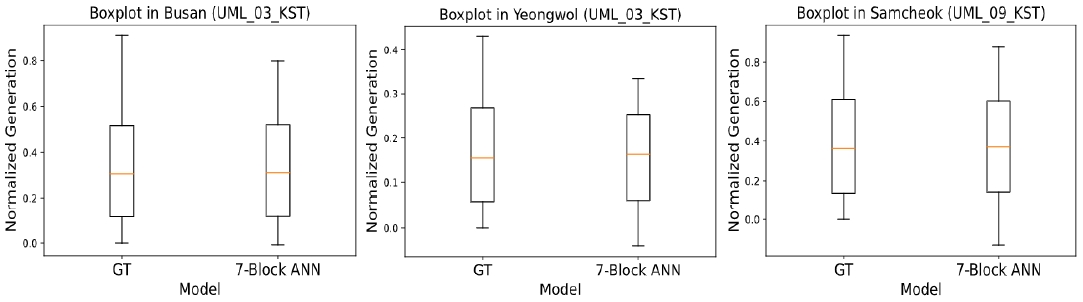
<Figure 21>의 좌측 그래프는 UML_03_KST이고 부산 지역일 때의 실제값(Ground Truth; GT)과 7-Block ANN 모델의 예측값 Plot을 나타내고, 우측 그래프는 UML_03_KST이고 영월 지역일 때의 실제값과 7-Block ANN 모델의 예측값 Plot을 나타낸다. <Figure 22>는 UML_09_KST이고 삼척 지역일 때의 실제값과 7-Block ANN 모델의 예측값 Plot을 나타낸다. <Figure 23>은 해당 NWP 모델과 지역의 실제값 분포와 7-Block ANN 모델의 예측값 분포를 나타낸다. <Table 7>은 해당 NWP 모델과 지역에 따른 실제값과 예측값 각각을 Kolmogorov- Smirnov Test한 결과이고 <Table 8>은 UML_03_KST인 부산, 영월 지역과 UML_09_KST인 삼척 지역의 실제값 집단과 7-Block ANN 모델의 예측값 집단 차이를 Wilcoxon Rank Sum Test한 결과이다.
<Figure 21>과 <Figure 22>를 보았을 때, 7-Block ANN 모델의 예측값이 해당 NWP 모델과 지역에서 실제값을 잘 예측하고 있음을 확인할 수 있다. 또한, <Figure 23>의 Box plot 그래프에서도 해당 NWP 모델과 지역의 실제값 분포와 7-Block ANN 모델의 예측값 분포가 유사함을 알 수 있다. 또한, 실제값 집단과 7-Block ANN 모델의 예측값 집단 간에 차이가 없음을 검정하기 이전에 정규성 검정을 하였다. 해당 NWP 모델과 지역에 해당하는 실제값, 예측값의 총 6개의 집단에 대해 Kolmogorov- Smirnov Test를 했다. <Table 7>을 보면, 각각의 집단에 대해 모두 P-value가 0.05보다 작았기 때문에 귀무가설을 기각했다. 유의수준 하에서 모든 집단은 정규분포를 따르지 않는다고 할 수 있으며, 집단 간의 차이를 검정하기 위해 분포의 가정이 필요하지 않은 Wilcoxon Rank Sum Test를 하였다. <Table 8>은 해당 NWP 모델과 지역의 Wilcoxon Rank Sum Test의 검정 통계량과 P-value를 나타낸다. 각각의 경우에 대해 P-value가 유의수준 0.05보다 컸기 때문에, 귀무가설을 기각하지 못했다. 따라서, 각각의 NWP 모델과 지역에서 실제값 집단과 예측값 집단 간에 유의미한 차이가 없다고 할 수 있다.
본 연구에서 제안한 7-Block ANN 모델은 NWP 모델에 관계없이 부산, 삼척, 인천, 영월, 하동 5개의 지역의 발전량을 전반적으로 잘 예측했으며, 개별 지역에 대한 성능 또한 대부분 지역에서 높았다. 7-Block ANN의 성능이 가장 높지 않았던 지역이 3곳 있었으나, 이에 대해서도 시각적, 통계적으로 잘 예측함을 보였다. 이러한 결과를 종합했을 때, 본 연구에서 제안한 7-Block ANN 모델은 대한민국 5개 지역의 발전소에서 충분히 사용될 수 있는 모델이라고 할 수 있다.
6. 결론 및 향후 과제
대한민국 5개 지역의 21곳 발전소에 대해 7가지 머신러닝 기반의 모델의 성능을 비교하였다. 특히, 본 연구에서는 과거 선행연구에서 제안된 머신러닝 기반의 모델들을 구조적으로 변형하여 실험했으며, 7가지의 다양한 모델의 성능을 비교하였다. 최종적으로 본 연구에서 제안한 7-Block ANN 모델이 대부분 지역에서 최고의 성능을 가졌으며, 최고의 성능을 내지 못한 지역에 대해서도 시각적, 통계적으로 실제값을 잘 예측하고 있음을 보였다. 이를 통해, 국내의 태양광 발전량 사업에서 7-Block ANN 모델이 유용하게 사용될 수 있다.
향후 과제 및 연구 방향은 다음과 같다. 본 연구의 데이터는 Time Series Data임에도 불구하고 Time Series 딥러닝 모델인 S2S 모델의 성능이 저조하였다. 본 연구의 평가는 태양광 발전이 종료되는 밤 시간을 제외하였다. 따라서 머신러닝 모델과 인공신경망 모델은 밤 시간의 샘플들을 제거하여 학습했다. 그러나 S2S 모델은 샘플이 일정한 Sequence 간격으로 유지되어야만 한다. 따라서 밤 시간의 데이터를 제거하지 않았고 이상값이 있는 경우에는 이를 대체값으로 채워 넣어 학습했다. S2S 모델은 학습한 Train Set과 평가한 Test Set 간에 이질성 문제가 발생했기 때문에 낮은 성능을 보였다. S2S 모델을 학습시키는 과정에서 이를 고려하여 학습한다면, 다른 모델에 비해 더 높은 성능 향상을 기대할 수 있을 것이다.
Acknowledgments
본 연구는 4단계 두뇌한국21에 의해 지원되었습니다. 이 논문은 2021년도 고려대학교의 지원을 받아 수행되었습니다.(No.K2107521, 제조 산업 데이터를 활용한 딥러닝 기반 이상 분할 탐지 기법 개발). 이 논문은 제1저자 이용택의 석사학위논문 내용을 포함하며 논문의 저작권은 대한산업공학회지에 있음.
References
-
Ahmad, M. W., Reynolds, J., and Rezgui, Y. (2018), Predictive Modelling for Solar Thermal Energy Systems: A Comparison of Support Vector Regression, Random Forest, Extra Trees and Regression Trees, Journal of Cleaner Production, 203, 810-821.
[https://doi.org/10.1016/j.jclepro.2018.08.207]

-
Cheng, H., Cao, W., and Ge, P. (2012), Forecasting Research of Long-term Solar Irradiance and Output Power for Photovoltaic Generation System, IEEE., 2012 Fourth International Conference on Computational and Information Sciences, pp. 1224-1227.
[https://doi.org/10.1109/ICCIS.2012.157]

-
Huang, C. J. and Kuo, P. H. (2019), Multiple-input Deep Convolutional Neural Network Model for Short-term Photovoltaic Power Forecasting, IEEE Access, 7, 74822-74834.
[https://doi.org/10.1109/ACCESS.2019.2921238]

-
Kayri, M., Kayri, I., and Gencoglu, M. T. (2017), The Performance Comparison of Multiple Linear Regression, Random Forest and Artificial Neural Network by using Photovoltaic and Atmospheric Data, International Conference on Engineering of Modern Electric Systems (EMES), IEEE, 1-4.
[https://doi.org/10.1109/EMES.2017.7980368]

-
Kim, J. W. (2019), A Solar Power Prediction Scheme Based on Machine Learning Algorithm from Weather Forecasts, The Journal of Korean Institute of Information Technology, 17(9), 83-89.
[https://doi.org/10.14801/jkiit.2019.17.9.83]

-
Mekhilef, S., Saidur, R., and Kamalisarvestani, M. (2012), Effect of Dust, Humidity and Air Velocity on Efficiency of Photovoltaic Cells, Renewable and Sustainable Energy Reviews, 16(5), 2920-2925.
[https://doi.org/10.1016/j.rser.2012.02.012]

- Mellit, A., Menghanem, M., and Bendekhis, M. (2005), Artificial Neural Network Model for Prediction Solar Radiation Data: Application for Sizing Stand-alone Photovoltaic Power System, IEEE, Power Engineering Society General Meeting, 40-44.
-
Pedro, H. T. C. and Coimbra, F. M. C. (2012), Assessment of Forecasting Techniques for Solar Power Production with no Exogenous Inputs, Solar Energy, 86(7), 2017-2028.
[https://doi.org/10.1016/j.solener.2012.04.004]

-
Ramsami, P. and Oree, V. (2015), A Hybrid Method for Forecasting the Energy Output of Photovoltaic Systems, Energy Conversion and Management, 95, 406-413.
[https://doi.org/10.1016/j.enconman.2015.02.052]

- Seo, Y., Lee, B., and Choi, Y. (2017), Machine Learing Model-based Photovoltaic Power Generation Forecasting Using Meteorological Data, Journal of the Korean Society for Environmental Technology, 18(3), 242-251.
- Shin, D. H. and Kim, C. B. (2018), Short Term Forecast Model for Solar Power Generation using RNN-LSTM, The Journal of Korea Navigation Institute, 22(3), 233-239.
-
Skoplaki, E. and Palyvos, J. A. (2009), On the Temperature Dependence of Photovoltaic Module Electrical Performance: A Review of Efficiency/Power Correlations, Solar Energy, 83(5), 614-624.
[https://doi.org/10.1016/j.solener.2008.10.008]

-
Son, H., Kim, S., and Jang, Y. (2020), LSTM-based 24-Hour Solar Power Forecasting Model using Weather Forecast Data, KIISE Transactions on Computing Pratice, The Korean Institute of Computing Practice, 26(10) 435-441.
[https://doi.org/10.5626/KTCP.2020.26.10.435]

- Sutskever, I., Vinyals, O., and Le, Q. V. (2014), Sequence to Sequence Learning with Neural Networks, arXiv preprint arXiv:1409.3215, .
-
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., and Rabinovich, A. (2015), Going Deeper with Convolutions, IEEE Conference on Computer Vision and Pattern Recognition, 1-9.
[https://doi.org/10.1109/CVPR.2015.7298594]

이용택 : 동국대학교 통계학과에서 2020년 학사학위를 취득하고 고려대학교에서 산업경영공학부 석사과정에 재학 중이다. 연구 분야는 Deep Learning, Sequence Data Modeling, Computer Vision이다.
한성원 : 고려대학교 산업 시스템 정보 공학과에서 2003년 학사학위를 취득하였다. Georgia Institute of Technology에서 2006년 Operation Research 석사학위, 2007년 Statistics 석사학위, 2010년 Mathematics 석사학위를 취득하고 2010년 Industrial Engineering과 Statistics 박사학위를 취득하였다. University of Pennsylvania, Department of Biostatistics and Epidemiology에서 Post-doctoral Researcher(2010.07-2012.06), Hoffmann-La Roche Inc., Department of Non-clinical Safety에서 Post-doctoral Fellow(2012.07~2013.08), New York University, Department of Population Health에서 Research Scientist(2013.08-2015.12), New York University, Department of Population Health에서 Senior Research Scientist(2016.01~2016.02)을 역임하고, 2016년부터 고려대학교 산업경영공학부 교수로 재직하고 있다. 연구분야 중 방법론 분야는 probabilistic graphical model, network analysis, deep learning 등이 있으며, 응용 분야로는 바이오 의료, 소재 정보학, 품질 모니터링, 텍스트 마이닝이 있다.