기계 학습을 이용한 셀 문턱 전압 분포 기반의 Soft Decision 센싱 레벨 예측
© 2021 KIIE
Abstract
Along with the rapid growth of the NAND flash memory market, the phenomenon of stacking 3D NAND flash memory is also steadily increasing. As the number of stacks increases, NAND flash memory will inherit different cell threshold voltage distributions for different physical characteristics. Furthermore, this phenomenon intensifies as the deterioration of data neglect is added. Considering the threshold voltage of these various cells, it becomes difficult to derive the sensing level during the operation of embedded memory products. In this paper, we propose a Sensing Level (SL) prediction method for making Soft Decision (SD) using machine learning. The proposed method experimentally confirmed the possibility of constructing a model that reflects the threshold voltage distributions of various cells. The prediction accuracy of the model confirmed an excellent performance of 94 to 99%, improving 36 to 52%p compared to that of the probability-based prediction method.
Keywords:
Distribution of Cell Threshold Voltage, Machine Learning, NAND Flash, Soft Decision, Sensing Level Prediction1. 서 론
낸드 플래시 메모리는 대용량, 빠른 접근 속도로 인해 스마트폰과 같은 모바일(mobile) 장치와 개인용 컴퓨터 및 엔터프이즈(enterprise) 서버(server)용 Solid-State Drive(SSD)에 널리 사용된다. 낸드 플래시 메모리의 적층 방식은 더 많은 데이터(data)를 저장하고 비트(bit) 비용을 줄이기 위해 평면에서 3D(Dimension)로 변경되고, 이와 더불어 단위 셀(cell) 당 저장하는 비트 수도 증가하고 있다. 단위 셀 당 최대로 저장할 수 있는 비트 수는 3-비트 레벨 셀(Three-bits Level Cell, TLC) 에서 4-비트 레벨 셀(Quad-bits Level Cell, QLC) 로 증가하고 있다. 낸드 플래시 제조 공정의 미세화와 셀 당 저장 가능한 최대 비트 수의 증가는 데이터 에러(error) 발생률 증가로 이어지고, 저장 장치에서 중요한 신뢰성 저하를 유발한다. 따라서 메모리 저장 장치를 안정적으로 유지하기 위해서는 강한 오류 정정 코드(Error Correction Code, ECC) 적용이 필요하다(Zhao et al., 2013).
메모리 읽기 동작의 결과인 데이터에서 한 비트의 에러도 존재하지 않는 무결성(integrity)의 보장은 제품의 수명 신뢰성(reliability) 관점에서 중요하다. 지난 10여 년간 낸드 플래시 메모리에 사용된 대표적인 오류 정정 코드인 Low-Density Parity-Check(LDPC) 는 데이터 무결성 보장에 있어서 뛰어난 성능을 보여주었다. Bose-Chaudhuri-Hocquenghem(BCH) 코드가 Hard Decision(HD) 체계로만 디코딩(decoding)을 수행하는 반면, Soft Decision(SD) 체계를 사용하는 LDPC의 오류 정정 능력은 HD 정보와 더불어, 비트 값에 대한 확률 정보인 Log-Likelihood Ratio(LLR) 을 추가하여 디코딩을 수행하기 때문에 가능하다. 에러 비트 유형은 센싱 레벨(Sensing Level, SL) 에 의해 강한(strong) 에러와 약한(weak) 에러로 결정되는데, 전체 에러 비트들 중에 강한 에러의 비율을 Strong Error Ratio(SER)라고 한다. SD 체계에서 중요한 LLR 정보는 SER과 높은 관련성이 있다(Wang et al., 2011). 따라서 SD 디코딩을 통한 메모리 저장 장치를 안정적으로 유지하기 위해서는 SER을 고려한 SL 예측 모델이 필수적이고 중요하다(Park et al., 2020).
셀 동작과 열화에 대해 보장되는 조건 범위 내의 사전 실험으로 확보된 다양한 셀 문턱 전압 분포를 통해 SL을 산출한다. 균등 분할 모델은 SL의 전체 범위를 균등 분할하여 구간별 대표 SL을 설정하여 구축할 수 있다. 균등 분할 모델의 성능은 셀 문턱 전압 분포의 가능 범위를 분할하는 SL의 개수에 의해 결정된다. 무수히 많은 구간으로 분할하여 SL을 확보한다면 정확도가 높아지고 오차는 줄어든다. 하지만, 읽기 동작에 대한 응답 시간의 제한이 있는 임베디드 메모리 제품에서 분할 구간의 수는 제한적일 수밖에 없다. SL 예측 가능 횟수가 3회 이하로 구축된 균등 분할 모델의 SL 정확도는 낮고 큰 오차를 보이는 문제가 있다.
SL 예측 가능 횟수가 제한적인 상황에서 균등 분할 모델의 낮은 정확도는 확률 개념 도입을 통해 일부 개선이 가능하다. 확률 개념의 도입은 사전에 확보된 SL의 분포로부터 SL들은 후보군으로 선정하는 방법을 의미한다. 확률 기반 모델은 빈도가 높은 SL들로 후보군을 선정하기 때문에 균등 분할 모델 보다 높은 정확도와 낮은 오차를 갖는다. 그러나 낸드 플래시 제조 공정 미세화가 지속되고 적층 수가 증가하면 물리적 특성 차이가 발생할 뿐만 아니라 데이터가 방치되는 등의 열화 현상이 생긴다. 이러한 환경에서 쓰여진(programed) 셀에서 전하(charge) 유실(leakage)이 더해지면서 SL 분포의 분산이 커지는 결과를 초래했다(Mizoguchi et al., 2017). SL 분포의 분산이 커짐에 따라 확률 기반 모델의 예측 SL 값의 정확도는 감소하는 추세이다. 또한, 균등 분할과 확률 기반 모델은 임베디드 메모리 제품 특성상 SL 예측 가능 횟수의 제한으로 인해 정확도 향상의 한계가 있다.
본 논문에서는 다양한 셀 특성으로 인한 분포의 분산이 커지는 상황에서 SD 체계의 성능에 결정적 역할을 주는 SER을 고려하여 SL을 예측하는 문제를 다룬다. 전통적인 SL 예측 방법 대비, 다음 3가지 목표를 달성하였다.
- ∙ 셀 개수 산정 기반의 목표 SER별 SL 확보 방법을 제안함.
- ∙ 목표 SER에 대해 SL을 예측하는 머신 러닝(Machine Learning, ML) 기반의 모델링 절차를 제안함.
- ∙ 확률 기반 모델 대비 제안된 ML 기반 모델의 정확도 향상 수준을 실험을 통해 확인함.
본 논문의 구성은 다음과 같다. 제2장에서는 배경 지식 및 관련 연구에 대해 소개한다. 제3장에서 SL 예측 모델을 학습하는 절차를 설명한다. 제4장에서는 제안하는 ML 기반의 SL 예측 모델의 가능성을 확인하기 위하여 확률 기반 모델의 정확도 대비 성능 향상 정도를 실험을 통해 확인한다. 제5장에서 결론을 도출하고 추후 연구방향을 제시한다.
2. 배경 지식 및 관련 연구
2.1 다양한 셀 문턱 전압 분포
낸드 플래시 메모리 셀의 플로팅 게이트(Floating Gate, FG) 에 전하(charge)를 트래핑(trapping)하여 데이터를 저장하는 동작을 쓰기(program)라고 한다. 반대로 FG에 주입된 전하를 빼내는 동작을 지우기(erase)라고 한다. 쓰기와 지우기의 반복적인 동작을 P/E(program/erase) 사이클링(cycling)이라고 하며, 해당 P/E 사이클링으로 인해 FG의 건강 상태는 점점 악화되어 간다(Cai et al., 2013). 데이터 방치(retention)는 셀이 쓰여진(programed) 상태로 방치 시간이 증가함에 따라 데이터의 에러가 증가하는 열화를 의미한다. P/E 사이클링과 데이터 방치는 플래시 메모리의 대표적인 열화들이다.
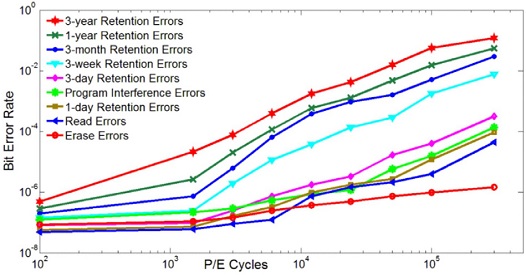
<Figure 1>은 P/E 사이클링과 방치 시간이 길어질수록 비트 오류율(Bit Error Rate, BER) 증가를 나타낸다. 그리고 FG에 트래핑 된 전하량이 많을수록 전하의 누출(leakage)은 더욱 빨라진다. 즉, 더 많은 전하량으로 쓰여진 셀은 방치 열화에 의해 더 많은 스트레스(stress)를 받는다는 의미이다(Kim, 2005).
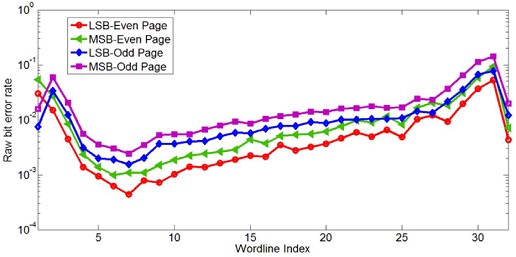
<Figure 2>는 낸드 플래시 메모리의 물리적 위치인 워드 라인(Word Line, WL)과 BER의 관계를 나타낸다. x축은 블록(block)의 WL 번호를 나타내고 y축은 해당 WL에서 페이지(page)의 BER을 나타낸다. 각 WL은 LSB-even, LSB-odd, MSB-even, MSB-odd를 포함하여 4 페이지로 구성된다. 4가지 페이지의 BER은 낸드 플래시 메모리의 물리적 위치인 WL 번호에 대해 동일한 경향을 보인다. WL 번호에 대해 BER의 경향이 동일한 이유는 공정 변동 효과 때문이다. 따라서 페이지의 BER은 WL 번호와 관계가 있다.
2.2 Flash Memory에서 LDPC의 기초
낸드 플래시 메모리는 페이지(page) 단위로 읽기(read)와 쓰기(program)를 동작한다. 최초 낸드 플래시 메모리 셀을 읽기 동작만 수행하면 셀 당 저장 가능한 최대 비트 수 증가로 인해 비트 오류율(BER)이 높아지기 때문에 데이터는 무결성은 보장되지 않는다. 데이터 무결성을 보장하기 위해서 오류 정정 코드(ECC)를 사용한다. 쓰기 과정에서의 ECC는 부가적인 페리티(parity) 데이터를 생성하여 페이지의 스페어(spare) 영역에 저장하는 방식으로 동작한다. 또한 낸드 플래시 메모리 컨트롤러(controller)에는 ECC 생성 모듈을 포함하고 있다.
LDPC ECC의 데이터 디코딩은 HD 방식과 SD 방식이 있다. HD 방식의 데이터 디코딩 과정은 인접한 셀 상태 간에 단일 센싱 레벨을 통해 비트 값을 결정한다. SD 방식의 데이터를 디코딩 과정은 HD 방식보다 훨씬 많은 센싱 레벨을 사용하여 비트 값의 확률 정보를 추가하여 비트 값을 결정한다. 많은 센싱 레벨을 사용하는 SD 방식은 항상 HD 보다 데이터 디코딩 속도가 느리지만 훨씬 높은 오류 정정 능력을 가지고 있다.
데이터 디코딩 과정에서는 오류 정정 능력은 낮지만 속도가 빠른 HD를 먼저 수행한다. 해당 데이터 디코딩 결과가 실패(fail)시, 속도는 느리지만 HD 보다 강력한 오류 정정 능력을 발휘할 수 있는 SD 방식을 추가로 수행하게 된다.
2.3 Sensing Level과 SER의 관계
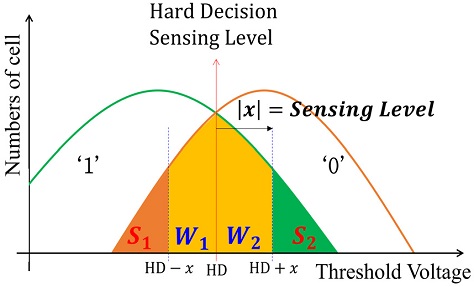
<Figure 3>은 센싱 레벨과 SER의 관계를 나타낸다. 가운데 빨간 선은 HD 방식의 센싱 레벨이다. 해당 센싱 레벨을 기준보다 낮은 문턱 전압을 가지는 셀들은 ‘1’로 판단하고, 높은 문턱 전압을 가지는 셀들은 ‘0’으로 판단한다. 녹색 분포를 기준으로 빨간 선보다 오른쪽에 위치하고 있는 면적이 존재한다. 면적 W2, S2의 해당하는 문턱 전압을 가지는 셀들은 에러 비트라고 판단된다. 하지만 W2와 S2는 HD 센싱 레벨인 빨간 전압을 기준으로 SD SL인 x만큼 더해지는 센싱 레벨을 통하여 에러의 종류는 Weak와 Strong으로 구분된다. Weak 에러는 HD 센싱 레벨과 SL 사이의 주황색 영역에 존재하는 에러를 의미하고, Strong 에러는 SL 영역을 벗어난 초록색 영역에 존재하는 에러를 의미한다. 분포에서 S1, W1, W2, S2 각 영역에 존재하는 에러 셀의 개수를 의미한다. SL이 좌/우로 이동하더라도 에러 셀의 전체 개수는 변하지 않으며, 단지 에러 종류의 변동만 발생한다. 즉, Weak 에러와 Strong 에러의 종류는 SL에 의해가 결정되고, SL의 변화에 따라 Weak 에러와 Strong 에러의 비율은 서로 반비례 관계이다.
높은 정정 능력을 갖는 LDPC ECC도 탑재되는 제품의 요구 스펙(spec)에 따라 정정 특성은 다르게 설계된다. Weak 에러에는 취약하지만 일정 수준 이하의 Strong 에러에 대해 강한 정정 능력 발휘하게 설계된 LDPC ECC의 경우, 설계 시 기대한 정정 능력 수준을 발휘하기 위해서는 Weak 에러의 개수는 감소시키고, Strong 에러의 개수는 증가시키는 방향으로 SL을 선택해야 한다. Strong 에러에 대해 높은 정정 능력을 보이도록 설계된 LDPC ECC라고 할지라도 일정 수준을 넘어선 Strong 에러 개수에 대해서는 디코딩 실패로 이어진다. 반대로 Strong 에러에는 취약하지만 일정 수준 이하의 Weak 에러에 대해 강한 정정 능력을 발휘하게 설계된 LDPC ECC의 경우, Strong 에러의 개수는 감소시키고, Weak 에러의 개수는 증가시키는 방향으로 SL을 선택해야 한다. 이 경우에도 일정 수준을 넘어선 Weak 에러 개수에 대한 디코딩은 실패하게 된다. 이러한 LDPC ECC 특성으로 인해 SL을 한쪽 방향으로만 증가 또는 감소시킬 수 없고, 일정 수준의 에러 종류의 개수를 넘어서지 않는 SL을 선택해야만 한다. 에러 종류에 대한 일정 수준의 에러 개수는 설계시에 다양하게 결정될 수 있으므로, 본 논문에서는 대표적으로 SER 30%, 40%, 50%에 대해 실험을 진행한다.
식 (1)은 전체 에러 비트들 중에 Strong 에러의 비율을 의미하고 이는 SER이라고 한다. S1과 S2의 차이는 원본 데이터 ‘1’이 읽기 동작에 의해 ‘0’으로 잘못 판단되고, 원본 데이터 ‘0’이 읽기 동작에 의해 ‘1’로 잘못 판단된 데이터의 상태를 나타낸다.
| (1) |
<Figure 3>에서 x값은 SL을 의미한다. SL의 증가는 식 (1)의 분자 부분인 S1+S2을 감소시키고, 이는 SER의 감소하게 된다. 반대로 SL의 감소는 S1+S2를 증가시키고, 이는 SER 값의 증가로 이어진다. 따라서 분포에서 셀 개수를 반영한 SL을 선택한다면, LDPC ECC 설계할 때 기대한 정정 능력 수준을 유지할 수 있게 된다.
2.4 균등 분할 모델과 확률 기반 모델
낸드 플래시 메모리의 쓰여진 셀의 문턱 전압은 방치 열화 정도에 따라 다양한 분포를 보이게 된다. 다양한 분포에 대해 SD 디코딩을 수행하기 위해서는 SL의 선택이 필요하다. 간단히 SL 예측 모델을 구축하는 방법은 SL의 가능 영역에 대해, n개의 영역으로 균등하게 나누어 n개의 SL 후보군으로 사용하는 것이다. 본 논문에서는 이러한 방식으로 구축한 모델을 균등 분할 모델이라 명명한다. 균등 분할 모델은 SL의 가능 영역의 개수 n을 크게 할수록 높은 정확도 보인다. 하지만 n개의 SL 후보군을 순차적 시도하다가 최악의 경우, n번째 시도만에 가장 적합한 SL로 디코딩을 수행하게 된다면 이는 메모리 읽기 동작의 엄청난 지연을 초래할 수 있다.
해당 한계를 극복하기 위한 방법으로 확률 분포와 통계의 개념을 도입하여 빈도가 높은 SL들을 분할하는 방식으로 균등 분할 방법보다 메모리 읽기 동작이 지연되는 위험을 줄일 수 있다. 뿐만 아니라, SL의 예측 정확도 향상도 기대할 수 있다. 하지만 여전히 확률 기반의 모델은 SL 예측 가능 횟수가 제한적이고, 셀 문턱 전압의 분포가 더욱 다양해지는 상황에서 높은 정확도를 보이기에는 한계가 존재한다.
3. 센싱 레벨(SL) 예측 모델
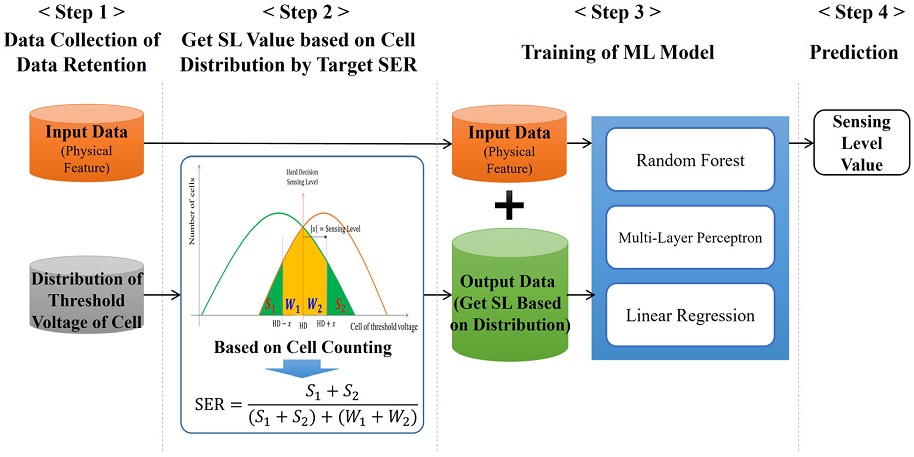
셀 문턱 전압 분포를 반영한 SL 예측을 위해 <Figure 4>와 같이 4단계로 구성된 모델을 제안한다. Step 1에서는 방치 열화 실험 데이터 수집 과정으로 장시간 데이터 방치 열화에 의해 변화하는 셀 문턱 전압 분포 데이터를 수집한다. Step 2에서는 목표 SER 별 셀 분포 기반의 SL을 셀 개수 산정을 통해 도출한다. Step 3은 ML 기반의 모델인 랜덤 포레스트(Random Forest, RF), 다층 퍼셉트론(Multi-Layer Perceptron, MLP), 선형 회귀(Linear Regression, LR) 에 대한 학습 과정을 진행한다. 마지막으로 Step 4에서는 학습된 ML 기반의 모델을 이용해 SL 예측을 수행한다.
3.1 방치 열화 실험 데이터 수집
본 논문에 사용된 데이터는 실제 3D TLC 낸드 플래시 메모리의 데이터로 총 331,190개이다. 강건한 예측 모델 구축을 위해서는 다양한 분포와 분산이 큰 데이터셋(data set) 구성이 필요하다. 따라서 데이터 방치 열화에 대해 다양한 셀 문턱 전압 분포와 큰 분산을 갖는 7번째와 8번째 상태(state) 사이의 RP7의 데이터로 실험을 진행하였다(Mizoguchi et al. 2017). 다양한 분포 변화에 대한 데이터 수집을 위해, 다양한 PE Cycle별로 0 ~ 1,000시간의 고온 데이터 방치 열화에 대해 24시간 주기로 물리적 특성 값과 셀 문턱 전압 분포 데이터를 수집하였다. 셀 문턱 전압 분포 데이터는 3.2절 SER별 셀 분포 기반의 SL 확보에 사용한다.
3.2 SER별 셀 문턱 전압 분포 기반의 SL 확보
<Figure 4>의 Step 2와 같이 셀 개수 산정 기반으로 목표 SER에 대한 SL을 도출한다. 셀 문턱 전압 분포에서 S1, W1, W2, S2의 셀 개수를 모두 합치면 전체 에러의 개수이다. S는 Strong 에러를 의미하고, W는 Weak 에러를 의미한다. S1, W1와 W2, S2의 구분은 HD 레벨을 기준으로 좌측을 S1, W1으로 우측을 W2, S2으로 구분한다. S1와 W1의 구분은 SL에 의해 결정한다. SER은 전체 에러 중에 Strong 에러의 비율을 의미한다. 셀 문턱 전압 분포 데이터를 수집하였기에 개수 산정 기반으로 목표 SER 수식이 만족하기 위한 S1, S2의 개수를 결정하는 SL의 도출이 가능하다. 모든 SER에 대해 모델 설계 가능함을 실험을 통해서 확인하기 위해 SER을 30%, 40%, 50%으로 나누어 결과 변수를 도출한다.
3.3 ML 기반의 모델 학습 및 예측
3.1절에서 확보한 독립 변수는 연속형 데이터이고 각 독립 변수의 크기(scale)의 차이가 심한 경우 ML 기반 모델의 예측 정확도 저하를 유발할 수 있다. 따라서 min-max 정규화를 통해 독립 변수를 0 ~ 1 사이로 정규화 하는 데이터 전처리를 수행한다. RF 모델에서 변수 중요도와 도메인 지식을 통해 중요 변수를 선택하여 동일하게 ML 기반 모델들의 훈련셋과 테스트셋으로 사용하였다. 다양한 방법을 통한 변수 선택 최적화는 추후 연구 과제로 남긴다. 3.1절에서 확보한 셀 문턱 전압 분포 데이터를 기반으로 3.2절의 목표 SER에 대해 확보한 결과 변수 SL은 연속형 데이터이다. 결과 변수 SL은 예측 오차에 대한 직관적인 설명력을 확보하기 위해 정규화를 수행하지 않았다.
<Table 1>은 중요 변수로 선택된 입력 변수 4종(Hard Decision Sensing Level, Word Line 값, Program/Erase 수행 횟수, Window 이내 셀 개수)과 출력 변수 1종(SL)으로 구성 되어있다. 셀 당 3bits을 저장하는 TLC에서는 셀 분포 8개와 각 분포의 교차 지점은 총 7개가 존재한다. Hard Decision Sensing Level은 인접한 두 셀 분포가 교차하는 지점의 Level 값이다. Word Line 값은 낸드 플래시 블록 내의 셀의 병렬 동작을 제어하기 위한 배선이다. 또한 위치에 따라 물리적 특성 차이가 존재하는 적층 구조인 낸드 플래시 메모리에서 적층 위치 정보를 의미한다. Program/Erase 동작 횟수는 현재까지 낸드 플래시 메모리 셀의 누적된 쓰기와 지우기 동작의 수를 의미한다. 셀 개수는 Hard Decision Sensing Level을 중심에서 좌/우로 특정 폭을 가진 창(window) 이내에 존재하는 셀의 개수를 의미한다. 이는 셀 열화가 진행됨에 따라 셀 분포의 변동이 발생하고, 이는 창 이내의 셀 개수와 관계가 있다. 출력 변수 SL은 3.2절에 기술된 방법으로 목표 SER에 대해 도출한 Sensing Level 값이다.
일반적으로 원시 데이터로부터 데이터 패턴을 학습하기 위해 학습셋(training set), 모델이 실제 시나리오에 따른 동작을 통한 모델 성능 확인을 테스트셋(test set)으로 구성하고, 튜닝 및 평가를 위한 단계로 검증셋(validation set)으로 구성한다. 하지만, 본 예측 모델은 ML 기반 알고리즘 학습에 적합성이 높다고 판단되었고, 낸드 플래시 메모리에서 ML 기반의 모델을 통해 셀 분포가 반영된 SL 예측이라는 새로운 응용 분야에 대한 시도이기에 학습셋(70%)과 테스트셋(30%)만으로 구성하여 예측 모델을 도출했다.
지도 학습은 입력 데이터와 그에 대한 출력 데이터를 포함하는 레이블(label)이 있는 데이터를 사용하여 학습을 진행하는 방법으로, 학습 데이터의 입력 데이터와 출력 데이터로 해당 시스템의 함수를 추론하여 새로운 입력이 들어왔을 때 해당 함수를 이용하여 대응하는 출력을 예측한다. 본 논문의 SL 예측은 연속적인 입력 데이터에 대해 연속적인 출력 데이터를 추론하는 회귀모델에 적합하다 할 수 있다. 딥러닝(Deep Learning)을 포함한 다양한 ML 기반의 회귀모델이 존재한다. SL 예측을 위한 모델에 대한 학습은 오프라인(off line)상에서 진행할 수 있다. 하지만 훈련셋을 이용하여 개발된 학습모델을 임베디드 메모리상에 탑재한 온라인(on line) 상에서 메모리 읽기 성능 저하를 최소화하여 SL 예측 수행이 가능하기 위해서는 계산량의 최소가 필요가 있다. 따라서 SL 예측 수행에 필요한 계산량을 최소화함과 동시에 우수한 예측 성능을 확보하기 위해서 RF, MLP, LR을 선정하였다. 데이터의 엔트로피(entropy) 기반의 의사 결정 나무(Decision Tree, DT) 의 앙상블(ensemble) 모델인 RF는 최대의 예측 성능 확인하기 위해 사용하였다. 또한 계산량 최소화를 위해 RF를 구성하는 DT의 수는 10으로, 트리의 최대 깊이는 5로, 최대 리프 노드(leaf node)의 개수는 10으로 제한하고 모델 학습을 진행한다. MLP는 활성화 함수로 tanh를 사용하고, 최적화 방법으로 adam을 사용하였다. 또한 계산량 최소화를 위해 은닉층의 개수는 2개, 은닉 노드 수는 5개로 제한하여 구성하였다. 이는 대표적인 퍼셉트론 모델의 예측 성능 확인을 위함이다. 최소 제곱 방식을 사용하는 LR 모델은 최소 연산으로 확보 가능한 예측 성능 수준을 파악하기 위해 사용하였다.
본 논문은 ML 기반 SL 예측 모델의 1회 예측의 정확도가 전통적인 예측 모델을 대체하여 사용 가능 여부를 확인하기 위해 진행하였다. 모델 별 계산량과 정확도의 관계 및 최적화된 모델의 학습/예측 소요 시간에 대한 확인은 추후 연구 과제로 남긴다.
3.4 평가 지표
일반적으로 수치를 예측하는 회귀 모델의 대표 평가 지표는 Mean of Absolute Error(MAE)와 Mean of Squared Error(MSE)이다. 추가로 정확도(accuracy) 확인을 위해 예측 값과 실제 값의 차이인 오차를 허용 구간으로 나누어 정확도 지표도 사용한다.
∙ MAE & MSE
식 (2)는 MAE의 수식이다. y는 실제 값이고 은 예측 값을 그리고 n은 전체 개수를 의미한다. 따라서 이 수식은 실제 값과 예측 값의 차이의 절댓값을 취하여 다 더한 값에 대해 전체 개수로 나눈 값으로 이는 오차 크기의 평균을 의미한다. 오차에 대해서 절대값을 취하기 때문에 가장 직관적으로 알 수 있는 평가 지표이다. 하지만 오차에 절대값을 취하기 때문에 예측 모델이 미달 추정이나 초과 추정 여부의 확인이 어렵다는 한계점이 있다.
| (2) |
식 (3)은 MSE의 수식이다. y는 실제 값이고 은 예측 값을 그리고 n은 전체 개수를 의미한다. 따라서 이 수식은 실제 값과 예측 값의 차이의 제곱을 취하여 다 더한 값에 대해 전체 개수로 나눈 값으로 이는 오차 제곱의 평균을 의미한다. 오차에 제곱을 취하기 때문에 크기를 산정할 수 있는 평가 지표이다. 하지만 오차의 크기 변화를 가져오므로 직관적인 오차 파악이 어렵다는 한계점이 있다.
| (3) |
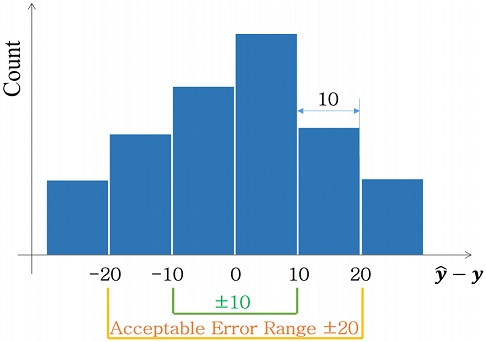
∙ 허용 구간에 대한 정확도
<Figure 5>는 직관적인 성능 파악을 위해 정확도를 산출하는 방법을 설명하는 그림이다. 예측 값에서 실제 값을 뺀 오차를 구간별로 나누어서, 0을 중심으로 전체 개수 중에 허용 구간 안에 비율을 계산하여 정확도로 산출하였다. 예를 들어 본 논문 실험에서 허용 구간 ±10은 예측 값과 실제 값의 차이가 -10 ~ +10 사이라는 것을 의미한다. 정확도는 허용 구간 안의 예측 오차의 개수를 전체 테스트 데이터 개수로 나눈 것이다.
4. 학습 모델 성능 평가
훈련셋을 이용하여 개발된 학습모델에 대해 테스트셋을 이용하여 3.4절의 평가지표(MAE, MSE, 정확도)로 성능을 평가를 진행하였다.
4.1 예측 모델 간 성능 비교
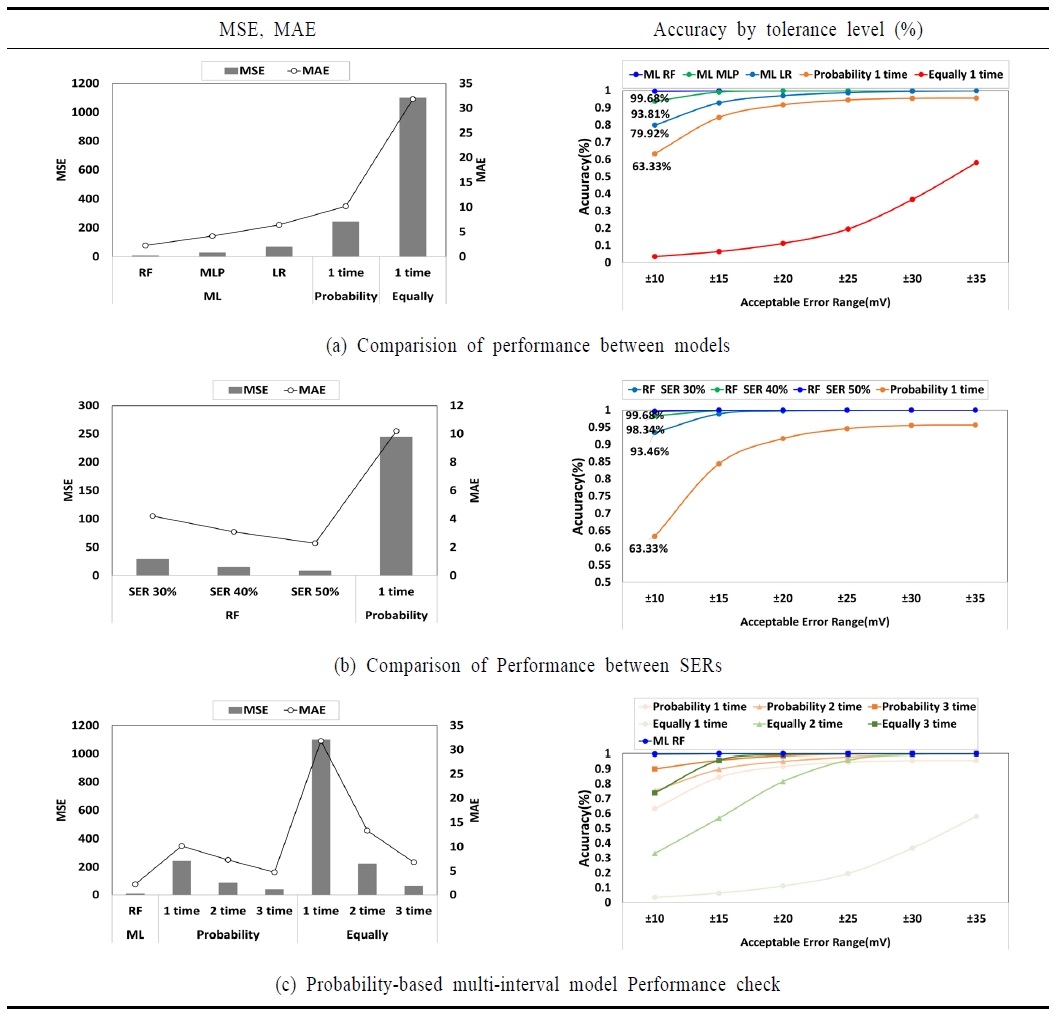
<Figure 6>은 SL 예측 모델 간 성능 비교 결과를 나타낸다. (a)는 모델 간의 성능 비교를 위해 SER 조건은 50%로 고정한 성능 결과이다. 또한 한번의 예측 기회에서의 ML 기반 모델의 성능의 수준을 동등 조건에서 비교하기 위하여 확률 기반 모델과 균등 분할 모델을 SL 예측 가능 횟수를 1회로 제한하고 실험을 진행하였다.
<Figure 6>의 (a) 왼쪽 그래프는 모델 성능 비교의 대표적인 평가 지표인 MSE와 MAE에 대한 결과이다. 평가 지표 MSE와 MAE가 작은 값을 갖는다는 것은 예측된 SL과 실제 SL의 차이가 작다는 것을 의미하며 RF 모델의 예측 성능이 가장 우수한 것으로 확인된다. 또한 모든 ML 기반 모델의 평가 지표는 확률 기반 모델이나 균등 분할 모델보다 낮은 것으로 확인된다. 이는 SL의 분포를 단순히 2등분하여 대표 SL 한 개를 사용하는 확률에 기반보다 ML 기반 모델의 예측 성능이 우수함을 보여준다.
<Figure 6>의 (a) 오른쪽 그래프는 실제 SL과 예측 SL 차이에 대해 ± 구간을 허용하고 확인한 정확도 결과이다. 오차에 대한 허용 구간의 크기가 커질수록 모든 모델의 예측 정확도의 향상된다. 하지만 균등 분할 모델은 ±35까지 오차를 허용하여도 정확도는 60% 수준이다. 이는 균등 분할 모델로 예측한 SL 오차 분포의 폭이 70 이상일 가능성이 높다고 추정할 수 있다. 반대로 RF 모델은 ±10 오차를 허용할 경우의 정확도 99%는 RF 모델의 예측 오차 분포의 폭이 20 이내에 들어올 가능성이 99%라는 의미를 갖는다.
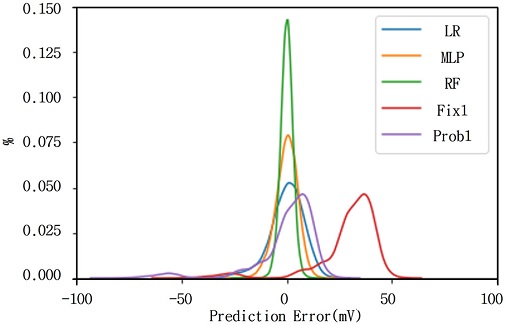
<Figure 7>의 RF 모델에 대한 예측 오차 분포를 보면 다른 모델에 비해 분산이 작고 평균이 0에 근사한 것을 시각적으로도 확인 가능하다. 하지만 균등 분할 모델은 하나의 고정된 SL을 사용하기에 오차의 분산이 크고 중심치가 0이 아닌 값에 집중되어 큰 오차가 다수 존재한다는 것을 알 수 있다.
임베디드 제품 특성으로 인해 SL의 개수에 제한되는 상황에서의 확률 기반 모델과 균등 분할 모델의 한계점이 실험을 통해 확인되었다. 그에 비해 ML 기반의 RF, MLP, LR 모델들의 1회 예측 성능은 우수하였고, 그 중 RF 모델의 예측 성능은 모든 평가 지표에서 가장 우수하였다. 특히 앙상블(Ensemble) 모델인 RF는 배깅(Bagging) 방식의 대표적인 알고리즘(Algorithm)이기 때문에 높은 예측 성능 달성이 가능하였다고 추정할 수 있다. 이는 셀 개수 산정 방법을 이용하여 목표 SER에 대한 ML 기반의 SL 예측 모델 구축이 가능하다는 것을 실험을 통해 확인할 수 있었다.
4.2 목표 SER별 ML 기반의 모델 간 성능 비교
<Figure 6>의 (b)는 4.1절에서 가장 우수한 예측 성능을 보인 RF 모델에 대해서 SER별 평가 지표 MAE, MSE와 정확도 비교 그래프이다. 동등 조건에서의 성능을 비교를 위해 확률 기반 모델의 SL 예측 가능 횟수를 1회로 제한하고 실험을 진행하였다.
<Figure 6>의 (b) 왼쪽 그래프에서 SER별로 평가 지표 MSE와 MAE는 유사한 수준이지만 미세하게 SER 30%보다 SER 50%에서 높게 확인된다. <Figure 3>에서 셀 분포가 정규분포의 형태를 띄는 것을 확인할 수 있고, 이로 인해 목표 SER이 감소함에 따라 SL은 Hard Decision Sensing Level을 기준으로 멀어지게 된다. 이는 정규 분포의 양쪽 끝 부분의 셀 개수는 중심부에 비해 적다. 적은 셀 개수로 인해 SL의 작은 변동에도 식 (1)의 분자 부분인 S1+S2의 변화폭은 커지게 되어 생기는 차이라고 추정된다. 미세한 성능 차이가 존재함에도 SER 30%에 대한 RF 모델의 성능은 확률 기반의 SL 예측 가능 횟수 1회인 모델 보다 압도적으로 우수한 수준으로 확인된다. 목표 SER의 감소에도 동등 수준의 예측 성능을 확보하는 방법은 추후 연구 과제로 남긴다.
<Figure 6>의 (b) 그래프에서는 오차 허용 구간 ±10에서 SER별 RF 모델은 SER 30%에서 93.46%가 가장 낮은 정확도로 확인된다. 이는 확률 기반의 모델 정확도인 63.33% 보다 월등히 높은 정확도이다.
모든 SER에 대해 RF 모델이 RF는 경우에 여전히 가장 낮은 MAE, MSE 평가 지표 수치와 93.46 ~ 99.68%의 높은 정확도 수준을 보이고 있다. 이는 ML 기반의 RF 모델은 목표 SER별 모델 구축이 가능하다는 것을 실험적으로 확인하였다.
4.3 다구간 확률 기반 모델 성능 확인
<Figure 6>의 (c)는 ML 기반의 모델들 중 성능이 가장 우수한 RF 모델의 성능 수준을 확인하기 위해 균등 분할과 확률 기반에 대해 SL 예측 가능 횟수를 최대 3개까지 확장시킨 성능을 비교하였다.
<Figure 6>의 (c) 왼쪽 그래프에서는 MSE, MAE 평가 지표 결과에서 균등 분할 모델이나 확률 기반의 모델도 SL 예측 기회가 3회까지 확장되면 성능이 향상됨을 확인할 수 있다. 이는 SL 분포에 대해 예측 가능 횟수가 늘어남으로써, 한 번의 예측으로 부담해야할 SL의 범위가 줄어들어 오차를 의미하는 평가 지표가 감소한 것으로 추정된다. 그럼에도 RF 모델은 확률 기반의 SL 예측 가능 횟수 3회인 모델 보다 우수한 성능으로 확인된다.
<Figure 6>의 (c) 오른쪽 그래프에서 균등 분할 모델은 SL 예측 가능 횟수를 3회로 확장한 정확도는 73.9%로 다소 저조한 성능 수준을 보인다. 하지만 확률 기반 모델의 SL 예측 가능 횟수가 3회까지 확장됨에 따라 정확도는 90.1% 수준까지 향상되는 것으로 확인된다. 균등 분할 모델에 비해 확률 기반 모델은 빈도에 근거하여 SL을 3회 시도함에 따라 SL 예측 성능이 우수한 것으로 추정된다. ML 기반의 RF 모델은 예측 가능 횟수가 1회임에도 불구하고 정확도 99.7%로 월등한 성능을 보인다.
ML 기반의 RF 모델의 정확도 수준은 균등 분할 모델과 확률 기반 모델의 예측 가능 횟수 3회를 능가하는 성능을 가지고 있음을 실험을 통해 확인하였다.
<Table 2>는 SER별(30, 40, 50%) 각 모델(ML, 확률, 균등분할)에 대해 테스트셋을 이용하여 평가지표(MAE, MSE, 정확도)로 성능을 정리한 표이다. 균등 분할 모델은 분할하는 구간이 확장됨에 성능이 향상되는 것으로 확인된다. 이는 분할 구간이 증가함에 따라 구간을 대표하는 SL의 담당 영역이 줄어들기 때문에 성능 개선 효과가 나타난다고 추정된다. 확률 기반 모델도 예측 가능 횟수의 증가에 따라, 성능이 향상되는 것으로 확인된다. 이는 균등 분할 모델의 성능 향상과 동일한 이유로써, 확률 기반으로 선정된 각 SL의 담당 영역이 줄어들었기 때문에 생기는 성능 개선 효과라고 추정된다. ML 기반 모델 중에서는 RF 모델의 성능이 가장 우수한 것으로 확인된다. 이는 의사 결정 나무의 앙상블로 구성된 RF 모델은 SL 예측에 대해 높은 정확도가 확보 가능할 수 있었다고 추정된다.
전체 모델 중, ML 기반의 RF 모델이 가장 우수한 성능을 보였다. 확률 기반 모델과 균등 분할 모델에 대해 RF 모델과 동일하게 예측 가능 횟수를 1회로 본다면 압도적으로 우수한 성능이 확인되고, 성능 향상 수준은 전통적인 모델들의 예측 가능 횟수를 3회로 확장시킨 성능보다 우세한 것으로 확인된다. 또한 허용 구간 ±15에서의 정확도는 99%로 확인되며, ML 기반 RF 모델의 우수한 예측 성능을 확인할 수 있다.
5. 결 론
본 논문은 머신 러닝을 이용하여 셀 문턱 전압 분포 기반으로 SD 동작 수행에 필요한 SL 예측 방법을 제시하였다. 데이터 방치 열화를 통해 다양한 셀 문턱 전압 분포에 대해 수집하고, 셀 문턱 전압 분포 데이터에서 셀 개수 산정을 통해 목표 SER에 대해 가장 적합한 SL을 확보하였다. 그리고 물리적 특성을 가진 인자를 입력 변수로 사용하고 목표 SER에 대해 적합한 SL을 결과변수로 도출하여 ML 기반 모델을 학습시켰다. 본 논문의 제안 방법을 통해 구축한 예측 모델의 성능은 전통적인 방법의 모델들 보다 우수한 성능을 보이는 것을 실험을 통해 확인하였다.
낸드 플래시 제조 공정의 미세화와 셀 당 저장 비트 수의 증가가 지속됨에 따른 신뢰성 특성 저하와 임베디드 제품에 대해 고성능이 요구되는 어려운 상황 속에서, 제안된 방법은 SL 1회 예측을 통해 반복 예측하는 전통적인 방법론들 보다 응답 속도와 정확도 측면에서 우수한 성능을 보인다. 또한 다양한 SER에 대해 모델링이 가능하기에 실용적이고 제품에 적용 가능할 것으로 기대된다.
본 논문에서는 ML 기반 모델들의 학습/예측에 사용된 데이터셋의 독립 변수는 RF 모델을 통해 선택한 중요 변수로 제한되었다. 향후에는 변수 선택에 대해 최적화 진행이 추가적으로 요구된다. 또한 학습된 ML 기반 모델의 예측은 한정된 제원을 가진 임베디드 메모리 상에서 수행되게 된다. 따라서 향후에는 각 ML 기반 모델의 하이퍼파라미터(hyperparameter)의 변화에 따른 예측에 필요한 계산량과 예측 정확도 사이의 관계, 그리고 학습/예측에 소요되는 시간에 대한 후속 연구가 필요하다. 마지막으로 2.3절에서 제안한 방법으로 SL 확보 시, 목표 SER의 감소에 따라 SL의 변동이 발생한다는 한계가 존재한다. 향후에는 목표 SER의 감소에도 동등 수준의 예측 성능을 확보할 수 있는 방법에 대한 연구가 필요하다.
Acknowledgments
이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원으로 수행된 연구(NRF-2019R1A2C2005949)이며, 4단계 두뇌한국21사업과 삼성전자(Samsung Electronics)의 지원을 통하여 수행되었음.
References
- Cai, Y., Haratsch, E. F., Mutlu, O., and Mai, K. (2012), Error Patterns in MLC NAND Flash Memory: Measurement, Characterization, and Analysis, In 2012 Design, Automation & Test in Europe Conference & Exhibition, 521-526
-
Cai, Y., Haratsch, E. F., Mutlu, O., and Mai, K. (2013), Threshold Voltage Distribution in MLC NAND Flash Memory: Characterization, Analysis, and Modeling, In 2013 Design, Automation & Test in Europe Conference & Exhibition, 1285-1290.
[https://doi.org/10.7873/DATE.2013.266]

- Kim, K. (2005), Technology for sub-50nm DRAM and NAND Flash Manufacturing, In IEEE International Electron Devices Meeting, 2005, IEDM Technical Digest, 323-326.
-
Mizoguchi, K., Takahashi, T., Aritome, S., and Takeuchi, K. (2017), Data-retention Characteristics Comparison of 2D and 3D TLC NAND Flash Memories, In 2017 IEEE International Memory Workshop, 1-4.
[https://doi.org/10.1109/IMW.2017.7939077]

-
Park, J., Lee, J. K., and Shin, H. (2020), Machine Learning Method to Predict Threshold Voltage Distribution by Read Disturbance in 3D NAND Flash Memories, Japanese Journal of Applied Physics, 59(8), 081003.
[https://doi.org/10.35848/1347-4065/aba5e0]

- Wang, J., Courtade, T., Shankar, H., and Wesel, R. D. (2011), Soft Information for LDPC Decoding in Flash: Mutual-information Optimized Quantization, In 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, 1-6.
- Zhao, K., Zhao, W., Sun, H., Zhang, X., Zheng, N., and Zhang, T. (2013), LDPC-in-SSD: Making Advanced Error Correction Codes Work Effectively in Solid State Drives, In Presented as part of the 11th {USENIX} Conference on File and Storage Technologies ({FAST} 13), 243-256.
노해동 : 한국항공대학교 정보통신공학과에서 2013년 학사학위를 취득하고 고려대학교에서 산업경영공학과 석사과정에 재학 중이다. 연구 분야는 Machine Learning Algorithms in Memory Products이다.
백준걸 : 고려대학교 산업경영공학과에서 1993년 학사, 1995년 석사, 2001년 박사학위를 취득하였다. 인덕대학교와 광운대학교에서 교수를 역임하였으며, 2008년부터는 고려대학교 산업경영공학과 교수로 재직하고 있다. 연구 분야는 Intelligent Diagnosis and Prognosis, Data Science for Manufacturing이다.