생산 라인 가용성 기반 반도체 생산 계획 최적화 모형
© 2025 KIIE
Abstract
Semiconductor manufacturing processes are characterized by high complexity and long lead times, making efficient production planning crucial. Existing methods using fixed and proportional lead times fail to adequately reflect production line variability. This study proposes an optimization model for semiconductor production planning that considers production line availability. The proposed model addresses this issue by distinguishing between available and non-available work-in-process (WIP). The suggested model was tested using a simulation method, which verified that it significantly reduces the discrepancy between planned and actual throughput, enhancing the feasibility of production plans while demonstrating superior performance in achieving high order fulfillment rates. Additionally, it maintained short lead times while reducing the variance in WIP and achieving high production volumes. This facilitates the company in managing its production line efficiently, thereby promoting improvements in productivity and profitability.
Keywords:
Semiconductor, Production Planning, Optimization, Simulation1. 서 론
반도체 산업은 현대 경제와 기술 발전에서 핵심적인 역할을 담당하고 있다. 반도체는 스마트폰, 컴퓨터, 자동차, 가전제품 등 다양한 전자 기기의 필수 부품으로, 이에 대한 수요는 지속적으로 증가하고 있다. 특히 인공지능, 사물인터넷, 5G 통신 등 첨단 기술의 발전에 따라 반도체 산업의 중요성이 더욱 부각되고 있다.
반도체 제조 과정은 FAB(Fabrication), EDS(Electrical Die Sorting), PKG(Packaging) 라인으로 구성되어 있다(Lee et al., 2005). 특히 FAB 공정은 그 복잡성과 긴 제조 공기로 인해 관리의 중요성이 더욱 강조된다. 따라서 각 공정 단계를 효율적으로 관리하기 위한 다양한 전략이 필요하다. FAB 공정은 200~300개의 다양한 공정을 거쳐 수백 대의 설비를 사용하며, 동일한 공정을 여러 번 반복하여 방문하는 특징을 가진 re-entrant 공정으로, 이로 인한 공정의 복잡성이 매우 높다(Choi et al., 2010). 각 레이어는 확산, 증착, 사진, 박막, 에칭 등의 다양한 세부 공정으로 구성되어 있으며, 이들 공정은 반도체의 특성을 결정하는 데 필수적이다(Kim, 2016). 이 공정들은 일반적으로 30일 이상 소요되는 긴 제조 공기를 필요로 하며(Seong, 2009), 이는 다른 공정에 비해 상대적으로 매우 긴 편이다. 이러한 복잡성 때문에 반도체 생산 계획은 일반적으로 12주에서 60주 사이의 기간 동안 주간 단위로 수립되며, 이 계획은 MPS(Master Production Schedule) 단계에서 세부적으로 분해되어 일일 스케줄로 구체화된다(Choi and Kim, 2015).
효율적인 생산 계획을 통해 기업은 자원을 최적으로 활용하고, 생산 비용을 최소화할 수 있으며, 이는 납기 준수, 고객 만족도 향상, 경쟁력 강화에 기여한다. 또한, 예측 가능성과 반응성을 향상시켜 시장 변화에 신속하게 대응한다. 특히, 긴 제조 공기와 높은 기술적 요구사항이 요구되는 반도체 산업에서는 생산 계획이 자원 배분, 재고 관리, 비용 효율성 등에서 중추적인 역할을 하며 전반적인 생산 효율성과 기업 수익성에 결정적인 영향을 미친다. 이러한 맥락에서 생산 계획의 정확성이 중요하다. 생산 계획은 전략적으로 회사의 운영을 가능하게 하며, 정확한 재공 수준을 예측하여 생산 계획의 실현 가능성을 높임으로써 생산성과 수익성 향상을 도모할 수 있다. 따라서, 반도체 제조 산업의 생산 계획은 이를 실행하는 제조 현장의 일정 계획 상의 차이를 최소화할 수 있는 운영이 매우 중요하며(Jeon, 2012), 이는 전체적인 생산 체계의 효율성을 극대화하는데 중요한 역할을 한다.
기존의 반도체 생산 계획 관련 연구에서는 널리 사용되는 방식으로 고정 제조 공기와 비율 제조 공기 두 가지 접근 방식이 있다. 고정 제조 공기 방식은 제조 공정 간의 이동 시간을 고정된 제조 공기로 간주하여 생산 계획을 모델링한다. Billington et al.(1983)은 제조 공기를 전 공정에서 다음 공정으로 넘어가는 고정된 시간으로 설정하고 이를 정수계획법을 통해 반영하는 생산 계획 모형을 제안하였다. 이 연구에서는 제조 공기를 주어진 기간의 최소 공배수로 가정하였다.
비율 제조 공기 방식은 제조 공기를 재공의 크기와 생산량의 비율로 계산하여 좀 더 유연성을 제공한다. 여기서 재공의 크기는 생산 공정에서 진행 중인 작업의 물량을 나타내며, 이는 생산 라인의 흐름과 작업 속도에 직접적인 영향을 준다. Graves(1986)는 초기 계획단계에서 설정한 제조 공기와 생산 라인의 재공 크기에 따라 생산량이 결정되는 방식을 통해 제조 공기를 반영하였다. Lee and Kim(2002)은 비 병목 공정에서 병목 공정으로 이동하는 비율을 제조 공기의 크기에 따라 결정하는 방식을 제안하였다.
위에서 제시한 두 가지 방식은 생산 라인의 변동성을 충분히 반영하지 못한다는 문제점이 있다. 따라서, 본 연구에서는 이를 해결하기 위해 생산 라인의 가용성을 반영한 모델을 제안하고자 한다. 제안하는 모델은 생산 계획 수립 시 생산 라인의 재공을 영업 요청량에 따라 가용성과 비가용성으로 구분하는 선도적인 접근 방식으로 생산 계획을 도출한다. 이를 통해 생산 계획의 실현 가능성을 높이고, 계획된 생산량과 실제 생산량 간의 차이를 줄임으로써, 생산량 예측의 오차가 감소함에 따라 재고 비용과 불필요한 생산 조정을 최소화할 수 있어 전체적인 운영 효율성을 높일 수 있다. 제안하는 모델은 시뮬레이션을 통해 기존 모델과 비교 평가한다.
본 논문의 구성은 다음과 같다. 제2장에서는 반도체 제조 생산 계획에 대한 기존 연구를 분석하고 본 연구의 목적을 명확히 한다. 제3장에서는 제안하는 모델을 상세히 설명하며, 제4장에서는 이 모델의 실험적 검증을 통해 기존 모델과의 성능 비교를 제시한다. 마지막으로 제5장에서는 본 연구의 결론과 향후 연구 방향에 대해 논의한다.
2. 선행연구
반도체 제조 공정에서 제조 공기의 관리는 생산 효율성에 직결되므로, 이를 최적화하기 위한 다양한 모델과 전략이 개발되고 있다. 제조 공기는 생산 계획과 스케줄링의 중요한 입력값으로 사용되며, 결과적으로 생산 계획의 실현 가능성을 평가하는 중요한 지표로 작용한다(Kim and Lee, 2009).
반도체 생산 계획에 있어서 제조 공기는 생산 계획의 실현 가능성에 영향을 주는 중요한 요소이다. 그러나 제조 공기를 정확하게 반영하는 데는 어려움이 존재한다. 제조 공기를 반영하기 위한 다양한 연구가 진행되었고, 기존 연구들은 고정 제조 공기, 비율 제조 공기 두 가지로 분류된다.
고정 제조 공기를 사용한 연구들을 살펴보면, Kim et al.(2002)은 쉬프트 기간 동안 각 병목 설비에서 생산할 제품의 양을 결정하는 최적화 모형을 제안하였다. 이 모형은 병목 설비에 도착할 예정인 재공의 양을 예측하며, 이 과정에서 재공이 표준 제조 공기를 따라 이동한다고 가정하였다. Habla et al.(2007)은 각 로트별 스케줄링을 만들어 병목 설비에 할당하는 최적화 모형을 제안했다. 이 모형은 병목 설비 간 이동에 필요한 최소 제조 공기를 정의하여 제조 공기를 입력값으로 사용하였다.
Billington et al.(1983)은 제조 공기를 앞 단계에서 다음 단계로 넘어가는 고정된 시간으로 설정하고 이를 정수계획법을 통해 반영하는 방식을 제안하였다. 이 연구에서는 제조 공기를 주어진 기간들의 최소 공배수로 가정한 모델을 제안하였다. 하지만 고정 제조 공기 방식은 생산 라인 전체에 재공이 균일하게 분포되었다는 가정이 존재하는데 이는 실제 생산 라인과 차이가 있다. 또한, 실제 생산 라인에서 제조 공기는 라인의 가동률과 라인의 재공 크기와 같은 요소에 의해 영향을 받게 되는데 제조 공기를 고정된 값으로 반영하는 경우 이러한 관계를 수리 모형에 반영할 수 없다는 문제점이 있다(Pahl et al., 2007).
제조 공기가 다양한 요소들에 의해 변동하기 때문에 제조 공기를 고정된 값으로 최적화 모형에 반영하지 않고 재공과 생산량을 통해 추정하는 방식으로 생산 계획에 반영하는 방법들이 제안되었다. 그중 비율 제조 공기 방식은 재공의 크기를 생산량으로 나눈 값으로 제조 공기를 반영하였고, 이를 통해 제조 공기의 변동성을 수리 모형에 반영한 연구들이 진행되고 있다.
Graves(1986)는 초기 계획단계에서 설정한 제조 공기와 생산 라인의 재공의 크기에 따라 생산량이 결정되는 방식을 통해 제조 공기를 반영하였고, Lee and Kim(2002)은 비 병목 공정에서 병목 공정으로 이동하는 비율을 제조 공기의 크기에 따라 결정되는 방식을 제안하였다. Kim and Lee(2009)는 생산량에 따라 제조 공기를 유지하기 위한 적정 재공의 양을 조정하여 제조 공기를 고려하는 방식을 제안하였다.
최근에는 인공지능을 활용하여 제조 공기를 보다 정확하게 예측하고 생산 계획에 반영하는 연구들이 진행되고 있다. Kramer et al.(2020)은 머신 러닝 모델을 사용하여 Job Shop 환경에서 리드타임을 예측하고, 이를 통해 생산 계획을 세워 정확성을 향상시켰다. 또한, Zhang(2024)은 머신 러닝 모델을 활용하여 반도체 부품의 리드타임과 표준편차를 예측하고, 이를 기반으로 안전 재고 모델을 개발하여 재고 부족 위험을 줄이고 대기 시간을 단축하였다. 그러나 이러한 인공지능 기반 방법은 리드타임의 변동성을 보다 정확하게 예측할 수 있지만, 초기 단계에서는 데이터 부족으로 인한 학습의 불완전성과 파라미터 설정의 어려움으로 인해 예측 정확도가 낮을 수 있다.
이와 달리 본 연구에서는 재공을 가용성과 비가용성으로 나눠 재공의 움직임을 생산 계획에 반영함으로써 생산 라인의 변동성을 고려하였다.
3. 문제 정의
반도체 생산 과정은 수백 개의 공정으로 이루어져 있으며, FAB 공정의 경우 긴 제조 공기로 인해 효율적인 생산 계획 수립이 필수적이다. 기존 연구들에서 제시한 모델에서는 제조 공기를 고정 또는 비율로 적용하였으며 이로 인한 문제점이 존재한다.
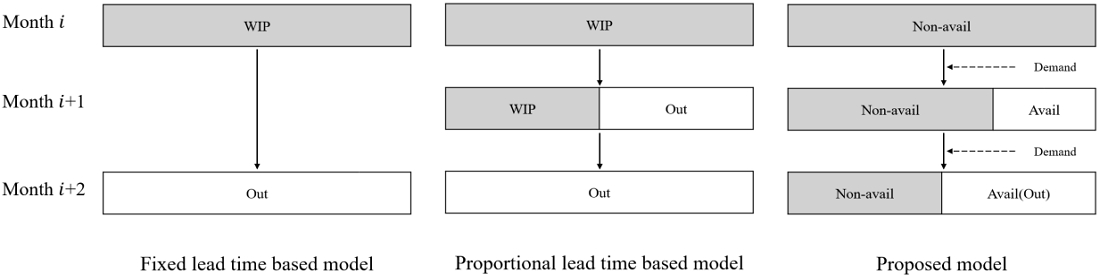
고정 제조 공기 기반 모델의 경우 제조 공정을 고정된 제조 공기로 간주하여 생산 계획을 수립하므로, 실제 생산 라인에서 발생하는 변동성을 충분히 반영하지 못한다. 실제로는 생산량과 재공의 크기 등 여러 요소에 의해 제조 공기가 변동되지만, 고정 제조 공기 기반 모델은 항상 일정한 기간이 지난 후에만 투입량이 출고 가능하다고 가정하였기 때문이다. 또 다른 방식인 비율 제조 공기 기반 모델의 경우 제조 공기를 재공 크기와 생산량의 비율로 계산하여 변동성을 일정 부분 반영하지만, 재공이 생산 라인 전체에 균일하게 분포되어 있다는 가정을 가지고 있어 실제 생산 라인과 차이가 있으며, 생산량에 비례하여 재공을 유지해야 하기 때문에 영업 요청량의 변동성이 커질수록 재공과 제조 공기의 변동성이 커지는 문제점이 있다.
본 연구에서는 이러한 문제점들을 해결하기 위해 라인의 재공을 가용 재공과 비가용 재공으로 나눈다. 제안하는 모델은 가용 재공과 비가용 재공으로 나눔으로써 가용 재공과 비가용 재공의 크기가 투입량과 출고량에 따라 변동된다. 또한, 출고량이 가용 재공의 크기에만 영향을 받기 때문에 더 적은 재공을 유지하면서도 출고량을 늘릴 수 있다.
<Figure 1>에서는 각 모델에서 반영한 재공 흐름을 나타내었다. 언급한 바와 같이 고정 제조 공기 기반 모델은 항상 일정한 기간이 지나면 투입된 재공이 출고되며, 비율 제조 공기 기반 모델은 항상 투입량에 비례하여 재공이 출고된다. 반면에 제안하는 모델은 수요 정보에 따라 비가용 재공을 가용 재공으로 변환하는 양을 조정함으로써 생산 라인의 변동성을 고려하였다.
3.1 반도체 생산 계획 최적화 모형
본 절에서는 본 논문에서 제안하는 선형 계획 기반의 반도체 생산 계획 모형을 제시한다.
- 인덱스 정보
- i: FAB
- j: Wafer
- t: 기간
- 데이터
- LCi: i번째 FAB 공정의 설비 생산 용량
- Djt : i번째 Wafer 종류, t번째 기간의 수요량
- 의사결정 변수
- : i번째 FAB, j번째 Wafer 종류, t번째 기간의 입고량
- : i번째 FAB, j번째 Wafer 종류, t번째 기간의 출고량
- availijt : i번째 FAB, j번째 Wafer 종류, t번째 기간의 가용 재공
- nonavailijt: i번째 FAB, j번째 Wafer 종류, t번째 기간의 비가용 재공
- kijt : i번째 FAB, j번째 Wafer 종류, t번째 기간에서 비가용 재공에서 가용 재공으로 처리되는 양
- : j번째 Wafer 종류, t번째 기간의 수요 부족량
- : j번째 Wafer 종류, t번째 기간의 초과 생산량
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
목적 함수 (1)은 영업 요청 대비 미충족량을 최소화하는 것이다. 제약식 (2)는 FAB 공정으로의 입고량이 포토 설비의 생산 용량을 초과하지 않음을 나타낸다. 제약식 (3)은 FAB 공정의 출고량이 가용 재공의 크기보다 작거나 같음을 나타낸다. 이는 출고량이 출고 가능량보다 작거나 같음을 의미한다. 제약식 (4)는 비가용 재공에서 가용 재공으로 전환되는 양이 포토 설비의 생산 용량을 초과하지 않음을 나타낸다. 제약식 (5)는 비가용 재공에서 가용 재공으로 전환되는 양이 비가용 재공의 양보다 작거나 같음을 나타낸다. 이는 출고 불가능량에서 출고 가능량으로 변환되는 양이 출고 불가능량보다 작거나 같음을 의미한다. 제약식 (6)은 FAB 공정에서 가용 재공의 크기를 계산하는 제약식으로, 전 기간의 가용 재공에 전 기간에 비가용 재공에서 가용 재공으로 이동한 양을 더한 후 이전 기간의 출고량을 뺀 양을 나타낸다. 제약식 (7)은 비가용 재공의 크기를 계산하는 제약식으로, 이전 기간의 비가용 재공에 전 기간에 FAB 공정으로 투입된 양을 더한 후 비가용 재공에서 가용 재공으로 전환된 양을 뺀 양을 나타낸다. 제약식 (8)은 목표 생산량 대비 최종 출고량의 편차를 계산하는 내용을 담고 있다. 제약식 (9)는 의사결정 변수가 비음 조건을 만족해야 함을 나타낸다.
4. 실험 및 결과분석
본 연구에서 제안하는 생산 계획 모델의 성능을 기존의 고정 제조 공기 기반 생산 계획 모델 및 비율 제조 공기 기반 생산 계획 모델과 시뮬레이션을 통해 비교하였다. 시뮬레이션의 환경은 Kim and Lee(2016)에서 사용된 반도체 제조 환경을 사용하였다.
실험에 사용된 FAB 생산 라인은 60대의 포토 설비로 구성되어 있으며, 10종의 웨이퍼 종류와 20개의 레이어를 가정하였다. 앞서 언급한 바와 같이 웨이퍼가 동일한 설비를 20번 방문하는 re-entrant 특성을 가지고 있다. 각 웨이퍼 종류와 레이어는 지정된 설비에서 처리된다. 각 설비가 웨이퍼를 처리하는 데 소요되는 시간은 웨이퍼 종류와 레이어에 따라 달라지며, [1–2.6] 시간 범위에서 유니폼 분포를 따른다. 또한, 각 레이어의 제조 공기는 [63–84] 시간 범위에서 유니폼 분포를 따르며, 평균은 약 3.07일이다. 각 설비는 각 레이어의 리드타임 동안 하나의 재공만을 처리하도록 설정되어, 각 레이어의 공정이 완료될 때까지 다른 작업을 수행하지 않는다.
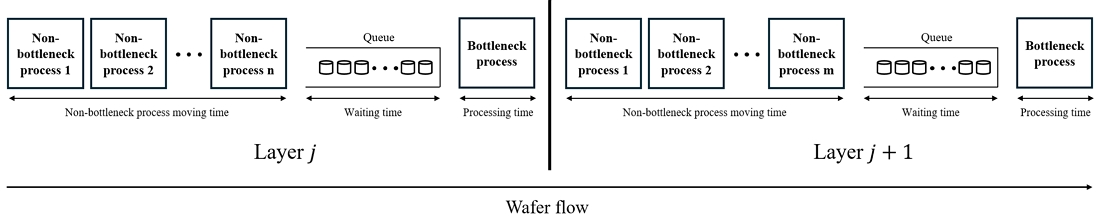
본 연구에서의 반도체 생산 환경은 <Figure 2>와 같이 주로 병목과 비 병목 두 가지 유형의 공정으로 나누어 각 공정의 특성을 반영한다. 병목 공정에서는 설비 사용량이 일정하지 않아, 비 병목 공정에서 웨이퍼 작업이 완료되는 시점을 정확하게 예측하는 것이 어렵다. 이는 병목 공정의 처리 속도 변화가 전체 생산 라인의 효율성에 영향을 미치기 때문이다. 포토 공정은 일반적으로 반도체 제조의 병목 공정으로 알려져 있으며, 여기서 발생하는 처리 속도의 변화는 다른 후속 공정에 영향을 미친다. 따라서 비 병목 작업의 제조 공기와 이동 시간은 σij·μ + exp((1−σij )·μ)로 가정되며, 여기서 σ는 처리 시간 비율(0 ≤ σij ≤ 1)이고 μ는 평균 처리 시간으로 정의한다. 이동 시간은 표준 처리 시간과 추가 시간으로 구성되며, 표준 처리 시간은 일정한 값으로 가정되고 과거 데이터를 이용해 산출된다. 비 병목 공정에서 웨이퍼가 작업을 기다리는 동안, 무기억성 특성으로 인해 예상 추가 시간은 시작 시간과 동일하게 유지된다.
제안하는 생산 계획 모델의 성능을 비교하기 위해 총 27개의 Case가 사용되었으며, 각 Case는 50개의 인스턴스를 사용하여 반복 실험을 수행하였다. 영업 요청량의 경우, 웨이퍼의 월평균 수요는 9가지(100, 150, 200, 250, 300, 350, 400, 450, 500)로 나뉘며, 각 평균 수요에 대해 3가지 변동성(10%, 20%, 30%)을 고려하였다. 60대의 포토 설비는 월 최대 웨이퍼 처리량을 600개로 설정하였다. 각 Case별로 기존의 고정 제조 공기 기반 방식 모델, 비율 제조 공기 기반 방식 모델, 그리고 제안한 방식의 모델을 통해 총 12개월에 대한 생산 계획을 생성하고, 이를 시뮬레이션을 통해 도출된 실제 생산량과 비교 평가하였다. 본 연구의 선형계획 모형은 Gurobi Solver 11.0.0 버전을 사용하였으며, Python 3.9.18 버전, AMD Ryzen 7 7700 프로세서가 장착된 시스템에서 수행되었다.
<Table 1>에서는 본 논문에서 제안하는 모델과 기존 모델의 각 Case별 계획된 생산량과 시뮬레이션을 통한 실제 생산량을 나타낸다. Demand는 웨이퍼의 월평균 수요량을 의미하며, Variability는 수요 변동성을 백분율로 나타낸 값이다. Optimization은 모델이 목적 함수를 만족하기 위해 계산된 이상적인 생산량을 의미하며, Simulation은 이를 실제 생산 환경에서 운영 조건과 변동성을 반영하여 도출된 실제 생산량을 나타낸다. Difference는 Optimization과 Simulation 간의 평균 생산량 차이를 절댓값으로 계산한 후 백분율로 나타낸 값이다.
비율 제조 공기 기반 모델의 경우, 평균 생산량의 차이가 13.5%로 나타나 계획 생산량과 실제 생산량 간의 차이가 상당히 크며, 고정 제조 공기 기반 모델은 7.3%, 제안하는 모델의 경우 5.0%의 차이를 보였다. 이는 제안하는 모델이 실현 가능성 측면에서 가장 효과적임을 보여준다.
추가적으로, 수요량이 낮을 때는 Optimization의 생산량보다 Simulation의 생산량이 더 크게 나타났으나, 수요량이 높아질수록 그 반대의 경향을 보였다. 이는 수요가 낮을 경우 재공량이 적어 생산이 원활하게 이루어지지만, 수요가 증가하면 투입량이 늘어남에 따라 재공량의 증가와 함께 변동성 및 대기 시간이 함께 증가하기 때문이다. 또한 수요가 포토 설비 생산 용량의 80% 수준일 때, 생산량 차이가 적음을 확인할 수 있다.
<Table 2>에서는 각 Case별로 영업 요청량 충족률, 평균 제조 공기, 재공량을 나타낸다. 먼저, 영업 요청량 충족률을 보면 고정 제조 공기 기반 모델은 평균 99.0%, 비율 제조 공기 기반 모델은 99.3%, 제안하는 모델은 99.6%로, 제안하는 모델의 영업 충족률이 가장 우수한 것을 확인할 수 있다.
평균 제조 공기는 웨이퍼의 입고부터 투입까지 소요된 시간을 총 생산량으로 나눈 후, 이를 일 단위로 환산하여 계산하였다. 평균 제조 공기를 비교해보면, 제안하는 모델이 비율 제조 공기 기반 모델보다 평균 14.4% 더 짧다. 그러나 실제 생산량을 보면 제안하는 모델이 비율 제조 공기 기반 모델보다 평균 2.7% 더 적게 생산하였다. 따라서, 제안하는 모델이 실제 생산량의 차이를 고려할 때, 이러한 제조 공기 단축 효과는 유의미하다고 할 수 있다.
마지막으로 평균 재공량을 살펴보면, 고정 제조 공기 기반 모델의 월평균 재공량이 483.9개, 비율 제조 공기 기반 모델이 583.0개, 제안하는 모델이 328.3개로, 제안하는 모델이 기존 모델들보다 더 작은 재공량을 유지함을 확인할 수 있다.
고정 제조 공기 기반 모델의 표준편차는 460.6, 비율 제조 공기 기반 모델의 표준편차는 414.4, 제안한 모델의 표준편차는 262.9로 제안한 모델의 재공량이 가장 일정함을 확인할 수 있다. 따라서 제안하는 모델은 평균 재공량이 적을 뿐만 아니라 재공의 분산과 범위도 작아 전반적으로 더 안정적인 모델임을 알 수 있다.
5. 결 론
본 논문에서는 재공과 생산용량의 관계를 반영하여 제조 공기의 변동성을 수리 모형에 통합하는 새로운 모델을 제안하였다. 시뮬레이션 실험 결과, 제안하는 모델은 다음과 같은 장점을 보였다. 첫째, 생산 계획의 실현 가능성 측면에서 해당 모델은 계획 단계와 실행 단계 간의 생산량 차이가 가장 적어 생산 계획의 실현 가능성이 높음을 확인할 수 있었다. 둘째, 영업 요청 충족률 측면에서도 해당 모델은 가장 높은 충족률을 보였다. 또한, 제안된 모델은 비교적 짧은 제조 공기를 가지면서도 재공량의 분산을 줄이며, 높은 생산량을 보였다.
그러나 제안하는 모델을 실제 현장에서 효과적으로 적용하기 위해 더 다양한 실제 생산 데이터를 반영할 필요가 있다. 실제 반도체 생산 라인을 단순화하여 시뮬레이션을 진행하였기 때문에, 시뮬레이션과 실제 생산 라인 간의 편차를 줄이면 제안하는 모델의 성능이 더욱 향상될 것이다. 따라서 시뮬레이션의 정밀도를 높이기 위해 더 다양한 실제 생산 데이터를 반영하고, 이를 통해 제안하는 모델의 성능을 더욱 정확하게 검증할 필요가 있다.
Acknowledgments
이 논문은 2023년도부터 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(No.2023-0-00076, SW중심대학(동아대학교)).
References
-
Billington, P. J., McClain, J. O., and Thomas, L. J. (1983), Mathematical programming approaches to capacity-constrained MRP systems: Review, formulation and problem reduction, Management Science, 29(10), 1126-1141.
[https://doi.org/10.1287/mnsc.29.10.1126]

-
Choi, B. K. and Kim, B. H. (2015), Simulation-based ‘Smart’ operation management system for semiconductor manufacturing. In Advances in Production Management Systems: Innovative Production Management Towards Sustainable Growth: IFIP WG 5.7 International Conference, APMS 2015, Tokyo, Japan, September 7-9, 2015, Proceedings, Part II (pp. 82-89), Springer International Publishing.
[https://doi.org/10.1007/978-3-319-22759-7_10]

- Choi, J., Sung, J., Noh, G., and Jeong, B. (2010), Optimal batch sizing for parallel machines in semiconductor wafer fabrication. In Spring Conference of Korean Institute of Industrial Engineers, 1515-1521.
-
Graves, S. C. (1986), A tactical planning model for a job shop, Operations Research, 34(4), 522-533.
[https://doi.org/10.1287/opre.34.4.522]

-
Habla, C., Monch, L., and Driebel, R. (2007, September), A finite capacity production planning approach for semiconductor manufacturing, In 2007 IEEE International Conference on Automation Science and Engineering, IEEE, 82-87.
[https://doi.org/10.1109/COASE.2007.4341734]

- Jeon, G. (2012), A study on simulation-based optimal production planning model of semiconductor through iterative parameter adjustment.
-
Kramer, K. J., Wagner, C., and Schmidt, M. (2020), Machine learning-supported planning of lead times in job shop manufacturing. In Advances in Production Management Systems, The Path to Digital Transformation and Innovation of Production Management Systems: IFIP WG 5.7 International Conference, APMS 2020, Novi Sad, Serbia, August 30–September 3, 2020, Proceedings, Part I, Springer International Publishing, 363-370.
[https://doi.org/10.1007/978-3-030-57993-7_41]

-
Kim, J. (2016), A study on equipment allocation scheduling rules for enhancing the efficiency of semiconductor equipment, Journal of Korean Society of Industrial and Systems Engineering, 39(1), 153-161.
[https://doi.org/10.11627/jkise.2016.39.1.153]

- Kim, S. and Lee, Y. (2009), An optimization model for production planning considering manufacturing lead time linked with production capacity, In Spring Conference of Korean Institute of Industrial Engineers, 1169-1176.
-
Kim, S., Yea, S. H., and Kim, B. (2002), Shift scheduling for steppers in the semiconductor wafer fabrication process, IIE Transactions, 34(2), 167-177.
[https://doi.org/10.1080/07408170208928859]

-
Kim, S. H. and Lee, Y. H. (2016), Synchronized production planning and scheduling in semiconductor fabrication, Computers & Industrial Engineering, 96, 72-85.
[https://doi.org/10.1016/j.cie.2016.03.019]

- Lee, D., Koh, H., and Kim, S. (2005), A study of strategy for planning of rework in semiconductor monitoring burn-in test process, Journal of Industrial Engineering (IE Interfaces), 18(3), 350-360.
-
Lee, Y. H. and Kim, T. (2002), Manufacturing cycle time reduction using balance control in the semiconductor fabrication line, Production Planning & Control, 13(6), 529-540.
[https://doi.org/10.1080/0953728021000014954]

-
Pahl, J., Voß, S., and Woodruff, D. L. (2007), Production planning with load dependent lead times: An update of research, Annals of Operations Research, 153, 297-345.
[https://doi.org/10.1007/s10479-007-0173-5]

- Sung, K. (2009), A study on capacity filtering algorithm based step plan generation method of semiconductor FAB.
- Zhang, C. (2024), Predicting semiconductor component lead-time for an oil and gas company: A dynamic safety stock model with machine learning (Doctoral dissertation, Massachusetts Institute of Technology).
Appendix
Appendix
- 데이터
- TAT: 웨이퍼의 제조공기
- 의사결정 변수
- eohijt : i번째 FAB, j번째 Wafer 종류, t번째 기간의 기말 재고량
- Fixed lead time-based model
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
- Proportional lead time-based model
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
고동우 : 동아대학교 산업경영공학과에서 2024년 학사학위를 취득하고 동아대학교 산업경영공학과에서 석사과정에 재학 중이다. 연구 분야는 최적화 및 인공지능이다.
이승훈 : 연세대학교 산업공학과에서 2021년 박사학위를 취득하고 현재는 동아대학교 산업경영공학과에서 조교수로 근무 중이다. 연구 분야는 제조, 서비스, 헬스케어, 국방 시스템 최적화이다.