[ Article ]

Journal of the Korean Institute of Industrial Engineers - Vol. 51, No. 2, pp.127-141

ISSN: 1225-0988 (Print) 2234-6457 (Online)

Print publication date 15 Apr 2025

Received 14 Sep 2024 Revised 17 Dec 2024 Accepted 05 Feb 2025

DOI: https://doi.org/10.7232/JKIIE.2025.51.2.127

누적 재구축 오차 기반 차량 노후화 지표

윤지현¹ ; 추창욱¹ ; 허종국¹ ; 임새린¹ ; 정현빈² ; 김성범¹^{, †}

1고려대학교 산업경영공학과
2현대 모비스 크리에이티브 UX셀

Vehicle Health Indicator Based on Cumulative Reconstructed Errors

Jihyun Yun¹ ; Changwook Chu¹ ; Jongkook Heo¹ ; Saerin Lim¹ ; Hyeon bin Jeong² ; Seoung Bum Kim¹^{, †}

1Department of Industrial and Management Engineering, Korea University
2Creative UX Cell Hyundai Mobis Co., Ltd.

Correspondence to: ^†김성범 교수, 02841 서울특별시 성북구 안암로 145 고려대학교 산업경영공학부, Tel: 02-3290-3397, Fax: 02-929-5888, E-mail : sbkim1@korea.ac.kr

Abstract

Constructing a health indicator for vehicles is becoming important for enhancing reliability and stability of operation systems. Typically, health indicator construction relies on supervised learning using each device’s end-of-life data. However, obtaining complete lifecycle data for automotive vehicles is challenging because of their long operational lifespans. This study proposes an unsupervised learning approach using a long-short term memory-based variational autoencoder (LSTM-VAE) to construct health indicators for vehicles using only early-life driving data. The VAE model learns the distribution of input data through reconstruction, allowing the detection of changes in data distribution due to aging by monitoring reconstruction errors. However, because VAE models may struggle to capture subtle data variations, this study integrates the concept of cumulative sum (CUSUM) control chart, which effectively detects minor changes of data distribution over time. Experimental results show that the CUSUM-based health indicator outperform the reconstruction error-based indicator in both quantitative and qualitative assessments. Notably, the health indicator demonstrates a clear response to specific component repairs or replacements, validating the practical effectiveness of the proposed approach in real-world vehicle operations. By enabling early detection of potential failures, this comprehensive vehicle health indicator can help reduce unexpected downtime and maintenance costs, ultimately improving the reliability and safety of automotive vehicles. This study is the first to develop a comprehensive vehicle health indicator using early-life data, verified with actual vehicle data, highlighting the practical applicability of PHM technology in the automotive industry.

Keywords:

Health Indicator Construction, Prognostic and Health Management, Integrated Vehicle Health Management, LSTM-VAE, Unsupervised Learning

1. 서 론

기계 시스템에서 수집되는 여러 센서 데이터를 실시간으로 모니터링하여 고장 및 이상 징후를 탐지하고 진단하거나, 잔여 유효 수명을 예측하는 건전성 예측 및 관리(prognostics and health management, PHM)는 항공 우주, 스마트 제조, 발전소, 운송 등 다양한 산업에서 기계 시스템의 신뢰성과 안정성을 높이고 운용 비용을 절감할 수 있는 핵심 기술로 주목받고 있다(Rezaeianjouybari and Shang, 2020; Zhang et al., 2019). 자동차 산업에서도 차량의 안전성과 신뢰성을 확보하고 운전자의 안전을 보장하기 위해서 다양한 관리 시스템들이 개발되었다. 특히, 1992년 미국 항공우주국에서 우주선 관리를 위해 제안한 통합 차량 건전성 관리(integrated vehicle health management) 개념이 일반 차량 관리에 도입되었다(Bhatti et al., 2021; Ranasinghe et al., 2022). 이를 통해 기존에 문제가 발생했을 때 작동하는 고장 진단(fault diagnosis) 기반 차량 관리 시스템은 차량 상태를 실시간으로 모니터링하여 고장 진단 뿐만 아니라 문제가 발생하기 전 미리 고장을 예측하고 차량을 관리하는 PHM 기반으로 차량 관리 시스템으로 패러다임이 변화하였다.

PHM 기반 차량 관리 시스템을 효과적으로 운영하기 위해서는 차량에서 수집되는 데이터로부터 현재 차량 상태를 정량화 할 수 있는 건전성 지표(health indicator, HI)를 구축하는 것이 중요하다. 과거에는 몇몇 센서 데이터에서 도메인 지식을 기반으로 직접 특징을 추출하거나 통계량을 활용하였지만, 센서 기술의 발달로 데이터가 복잡해지면서 이를 효과적으로 처리하기 위해 딥러닝(deep learning) 기술을 결합하는 건전성 지표 구축 연구가 진행되고 있다(Bajarunas et al., 2024; de Pater and Mitici, 2023; Li et al., 2018; Lövberg, 2021; Malhotra et al., 2016; Qin et al., 2021; Roman et al., 2021; Seitz et al., 2023; Ye and Yu, 2021). 하지만 현재까지 제안된 건전성 지표 구축 방법론들은 기계 시스템의 생애 전반에 대한 모니터링 데이터(생애 데이터)를 필요로 하기 때문에 자동차와 같이 수명이 길어 생애 데이터를 수집하기 어려운 분야에는 적용하기 어렵다는 문제가 있다. 실제로, 현재 자동차 분야에서는 이러한 문제로 인해 건전성 지표의 중요성에도 불구하고 배터리와 같은 특정 부품에 대해서만 연구가 이루어지고 있다(Alamelu Manghai and Jegadeeshwaran, 2019; Hu et al., 2020; Li et al., 2022).

본 연구에서는 이 문제를 해결하기 위해 long-short term memory-based variational autoencoder(LSTM-VAE)(Bowman et al., 2015)를 활용하여 차량의 초기 생애 데이터 만으로도 건전성 지표를 구축할 수 있는 비지도 학습 기반 방법론을 제안한다. 먼저, 노후화가 진행됨에 따라서 차량에서 수집되는 데이터 분포가 변화할 것이라 가정하고, 차량의 초기 생애 데이터만을 활용하여 LSTM-VAE를 학습시킨다. 이때 초기 생애 데이터는 노후화가 거의 일어나지 않은 데이터 분포로 볼 수 있다. 이후 노후화가 일어난 데이터를 학습이 완료된 모델에 입력하면, 노후화로 인해 데이터 분포가 변화하여 재구축이 제대로 이루어지지 않게 되고, 높은 재구축 오차(reconstruction error)를 반환하게 된다. 본 연구에서는 일차적으로 이 재구축 오차를 건전성 지표로 활용한다.

하지만 LSTM-VAE와 같은 재구축 모델은 미세한 데이터 분포 변동을 잡아내기 어렵다는 문제가 있다(Tang et al., 2020; Xu et al., 2022). 즉, 차량의 노후화로 인한 분포 변화가 매우 점진적으로 일어나는 특성을 반영하기 어려우며, 실제 실험에서도 이러한 경향을 확인할 수 있었다. 이를 해결하기 위해 본 연구에서는 통계적 공정 관리에서 많이 활용되는 누적합 관리도(cumulative sum chart, CUSUM)(Koshti, 2011) 개념을 활용하였다. 누적합 관리도는 단순히 현재 표본값을 통해 공정을 관리하는 슈하르트 관리도(shewhart chart)(Montgomery, 2019) 와 달리, 표본값과 목표값의 차이를 지속적으로 더해 나가는 누적 형식의 관리도이다. 이 방법은 시간에 따라 현재 공정의 변화 정도를 누적하므로, 슈하르트 관리도에서는 탐지하기 어려운 미세한 공정 변화도 쉽게 탐지할 수 있다는 장점이 있다. 본 연구에서는 누적합 관리도의 개념을 재구축 오차 기반 건전성 지표에 결합하여, 누적합 기반 건전성 지표를 제안하였다. 초기 차량 데이터 분포가 입력되었을 때 재구축 모델이 반환하는 평균적인 재구축 오차를 목표값으로 설정하고, 이 목표값을 기준으로 시간에 따라 재구축 모델이 반환하는 재구축 오차와의 차이를 지속적으로 더하며 이를 건전성 지표로 활용한다.

본 연구에서는 약 13,000km가량 운행한 실제 차량의 주행 데이터를 활용하여 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표를 평가하였다. 이 과정에서 차량의 여러 부품들이 각기 다른 생애 주기를 가진다는 점을 고려하여, 부품들을 크게 제동 시스템, 가속 시스템, 조향 시스템, 타이어 시스템으로 분류하고, 각 시스템별 건전성 지표를 구축하고 평가하였다. 실험 결과, 누적합 기반 건전성 지표가 단순 재구축 오차 기반 건전성 지표보다 정량적, 정성적 평가에서 모두 우수한 성능을 보였다. 특히, 누적합 기반 건전성 지표는 데이터의 가동 횟수에 따라 우상향하는 것을 확인함으로써 제안하는 건전성 지표에 대한 효용성을 입증하였다. 본 연구에서 정의하는 건전성 지표는 장비의 노후화 정도를 나타내는 수치로, 이 지표는 장비의 가동 횟수가 늘어남에 따라 점진적으로 상승하는 것이 타당하다. 즉, 가동 횟수가 증가함에 따라 노후화가 진행되므로, 건정성 지표는 이에 비례하여 우상향 곡선을 그리며 커지는 것이 합리적이다.

본 연구에서 제안하는 차량 건전성 지표는 단순히 차량 상태 파악을 넘어, 유지보수 시점을 사전에 예측하고 부품 교체 및 수리 계획을 효율적으로 수립할 수 있도록 함으로써 자동차 산업을 포함하여 생애 주기가 길어 총 생애 데이터를 구하기 어려운 다양한 산업 분야에서의 PHM 기술 활용을 더욱 촉진할 수 있을 것으로 기대된다.

본 논문의 기여점은 다음과 같이 요약할 수 있다.

∙ LSTM-VAE의 재구축 오차 특성을 활용하여, 차량과 같이 생애 주기가 긴 기계 시스템에 적합한 재구축 오차 기반 건전성 지표 구축 방법론을 제안하였다. 기존 방법론들이 전체 생애 데이터를 필요로 하는 것과 달리, 본 연구에서 제안한 방법론은 초기 생애 데이터만으로도 건전성 지표를 구축할 수 있다는 장점을 가지고 있다.
∙노후화로 인한 미세한 데이터 분포 변화를 탐지하기 위해 누적합 관리도 개념을 활용하여 단순 재구축 오차 기반 건전성 지표의 한계를 보완할 수 있는 누적합 기반 건전성 지표를 제안하였다. 제안한 누적합 기반 건전성 지표가 가동 횟수에 따라 점진적으로 우상향 하는 것을 확인함으로써, 제안 건전성 지표가 차량 시스템의 노후화를 측정하는데 효과적임을 입증하였다.

본 논문의 구성은 다음과 같다. 제2장에서는 자동차 산업을 포함하여 여러 산업 분야에서 제안된 PHM 시스템과 건전성 지표 구축 연구를 소개한다. 제3장에서는 본 연구에서 활용된 차량 주행 데이터 설명, 재구축 모델링, 누적합 프로세스 등 제안 건전성 지표 구축 과정을 설명한다. 제4장에서는 실험 결과를 통해 제안한 건전성 지표의 효용성을 정량적, 정성적으로 보여주고, 마지막으로 제5장에서는 결론을 서술한다.

2. 관련 연구

2.1 건전성 예측 및 관리(Prognostics and Health Management)

PHM은 기계 시스템에서 수집된 다양한 데이터를 모니터링하고, 이를 바탕으로 고장 및 이상 징후를 탐지하고 진단하며, 잔여 유효 수명을 예측하는 기술로, 다양한 산업 분야에서 활발히 연구되고 있다. 초기 PHM연구는 주로 도메인 지식이나 전문가의 경험을 활용하여 기계 시스템의 상태를 평가하고 진단하는 도메인 기반 방법론이 주를 이루었다. 그러나 도메인 기반 방법론은 전문가의 지식과 경험에 대한 의존성이 크고, 확장성이 부족하다는 단점이 있다(Gao et al., 2015).

이후 센싱 기술의 발달로 기계 시스템에 대한 다양한 데이터를 수집할 수 있게 되면서, 이러한 데이터를 바탕으로 기계 시스템의 열화 과정을 물리적, 수학적으로 모델링하여 상태를 평가하고 진단하는 모델 기반 방법론이 주요 연구 방향으로 자리잡았다(Jia et al., 2018). Byington et al.(2004)은 액추에이터(actuator) 고장 감지 및 예측을 위해 모델 기반 접근 방식을 개발하였다. 해당 연구는 물리적 모델링과 고급 매개변수 식별, 고장 감지 및 예측 알고리즘을 활용하며, 비행 제어 명령/응답 데이터만으로 초기 고장 감지를 신뢰성 있게 수행한다는 장점을 보였다. 또한 Daigle and Goebel(2013)은 원심 펌프의 상세한 물리 기반 모델을 구성하고, 모델 기반 예지 알고리즘을 적용하여 여러 손상 메커니즘이 활성화된 경우에도 효과적으로 잔여 유효 수명(remaining useful life)을 예측할 수 있는 모델 기반 PHM을 제안하였다. 이 접근법은 입자 필터(particle filter)를 사용하여 공동 상태-매개변수(state-parameter estimation) 추정을 수행하고, 불확실성 관리를 지원하는 확률적 프레임워크를 통해 기계 장비의 수명 종료(end of life)나 잔여 유효 수명을 예측할 수 있다는 장점이 있다. 하지만 이러한 모델 기반 방법론은 기계 시스템의 상태를 물리적 및 수학적으로 모델링 하기 위해 깊은 도메인 지식이 요구되며, 다양한 작동 조건을 모두 반영해야 효과적인 모델을 구축할 수 있어 기계 시스템이 복잡해질수록 적용하기 어렵다는 한계가 있다(Gao et al., 2015).

최근에는 앞서 언급한 한계점을 극복하기 위해 데이터를 분석하고 패턴을 찾아 기계 시스템의 상태를 평가 및 진단하는 데이터 기반 방법론이 연구되고 있다. 특히 수많은 데이터를 기반으로 스스로 학습하는 기계 학습(machine learning) 기법을 적용하려는 시도가 증가하고 있다(Ahmadzadeh and Lundberg, 2014). Wang et al.(2010)은 자동차 엔진의 진동 결함을 효과적으로 탐지하기 위해 단순한 구조를 가진 extension neural networks를 활용하였다. Luo et al.(2010)은 잠김 방지 제동 시스템 (antilock braking system)의 결함을 감지하기 위해 SVM을 사용하였고, Sankavaram et al.(2012)은 회생 제동 장치(regenerative braking)의 결함을 관리하기 위해 SVM과 k-nearest neighbor을 활용한 결함 탐지 모델을 개발하였다. 또한, Ghimire et al. (2011)은 전동 파워 스티어링 시스템(electric power steering system)의 고장 진단을 위해 SVM 모델을 사용하여 결함의 심각도를 효과적으로 추정할 수 있는 PHM 방법론을 제안하였다.

Xu et al.(2013)은 복잡한 항공기 엔진 시스템에서 잔여 유효 수명을 추정하기 위해 도메인 및 데이터 기반 PHM을 융합한 프레임워크를 제안하였다. 이 연구에서는 먼저 도메인 지식으로 항공 엔진 센서 데이터에서 모니터링할 매개변수를 선정하고, 고장 기준을 정의하여 학습 데이터를 구축하였다. 그런 다음, 구축된 데이터셋을 통해 support vector machine(SVM)이나 recurrent neural networks(RNN)와 같은 기계 학습 기법들을 활용해 효과적인 PHM 모델을 구축하였다. Li et al.(2018)은 스마트 그리드(smart grid)의 변압기 시스템에 대한 고장 진단을 수행하는 PHM 모델을 구축하기 위해 기계 학습 기반 방법을 제안하였다. 이 연구에서는 모델 학습 과정에서 역전파 신경망을 최적화하기 위해 cuckoo search 알고리즘을 적용하여 높은 성능의 고장 진단 모델을 개발하였다. Jalayer et al.(2021)은 회전 기계의 고장 탐지와 진단을 예측하기 위해 convolutional neural networks(CNN)과 long-short term memory(LSTM)을 결합하여 모델이 시간적 특징과 공간적 특징을 효과적으로 함께 학습할 수 있도록 설계하였다. 이 연구에서는 회전 기계의 진동 신호를 주파수 및 시간-주파수 도메인으로 변환함으로써, 기계 고장 특성의 복잡한 패턴을 더 정확하게 학습할 수 있도록 하였다. Qian et al.(2022)은 PHM에서 autoencoder 기반 접근법의 방향성을 제시하며, 이를 통해 산업에서의 고장 탐지 및 진단에 autoencoder 모델이 어떻게 활용될 수 있는지를 논의하였다. 특히 해당 접근법은 데이터의 비선형적 특성을 효과적으로 학습할 수 있으며, 이상 데이터 탐지를 위한 재구축 오차의 활용 가능성을 강조하였다. Oh et al.(2024)은 variational autoencoder(VAE) 모델과 누적합 관리도의 개념을 결합하여 선박 자동 식별 시스템(automatic identification system, AIS) 데이터의 이상 탐지 방법론을 제안하였다. 해당 연구는 누적합 관리도를 활용하여 이상 발생 시점을 실시간으로 감지하는 데 중점을 두었으며, VAE 기반 재구축 오차의 강건성을 다양한 상황에서 평가함으로써 데이터의 동적 특성을 효과적으로 반영할 수 있는 방법론을 제시하였다. 반면, 본 연구는 초기 주행 데이터만을 활용하여 차량 시스템의 노후화 정도를 정량적으로 반영할 수 있는 누적합 기반 건전성 지표를 제안한다. 제안하는 방법론은 VAE에 누적합 관리도의 개념을 적용하여, 노후화가 거의 진행되지 않은 초기 주행 데이터를 통해 시스템의 초기 상태를 학습한 후, 노후화로 인한 데이터 분포 변화와 이를 반영한 재구축 오차를 기반으로 건전성을 평가한다. 이 지표는 단순히 이상 데이터를 탐지하는 데 그치지 않고, 차량 시스템의 전반적인 상태와 노후화 진행 상황을 정량적으로 평가할 수 있도록 설계되었다. 이는 특정 시점의 단기적인 이상 탐지를 넘어, 차량 시스템의 상태를 지속적으로 모니터링함으로써 장기적인 건전성 평가와 노후화 예측을 가능하게 한다. 이러한 접근은 차량과 같이 생애 데이터 수집이 어려운 기계 장치에서도 활용이 가능하다는 점에서 중요한 기여를 한다.

2.2 건전성 지표 구축(Health Indicator Construction)

앞서 언급했던 것처럼 PHM은 수집된 데이터를 통해 기계 시스템의 상태를 평가하고, 이를 바탕으로 고장 진단, 잔여 유효 수명 추정 등 다양한 과업을 수행한다. 이러한 과업들이 효과적으로 작동하기 위해서는 기계 시스템의 상태를 정량화 하는 건전성 지표가 제대로 구축되어야 하며(Yu et al., 2019), 그 중요성 때문에 건전성 지표 구축 자체가 하나의 연구 분야로써 다뤄지고 있다. 최근에는 PHM과 마찬가지로 수집된 모니터링 데이터에서 현재 기계 시스템의 상태를 표현하는 특징을 추출하고 정량화 하는 데이터 기반 방법론들이 활발히 연구되고 있다. 예를 들어, Gebraeel et al.(2005)은 베어링(bearing)의 잔여 수명 분포를 추정하기 위해 베어링의 열화 과정을 지수 함수로 가정하고, 베이지안 기법(Bayesian approach)을 통해 건전성 지표 모델을 구축하는 통계적 모델링 방법을 제안하였다. Orchard and Vachtsevanos(2009)은 기계 시스템의 동적인 상태를 대변하는 상태 공간 모델(state-space model)을 정의하고, 이를 입자 필터 방식으로 학습하는 방법론을 제안하였다. 그러나 이러한 통계적 기법은 특정 통계적 가정에 대한 의존성이 크며, 많은 모니터링 데이터에서 도메인 지식을 기반으로 중요한 변수를 선택 및 추출해야 한다는 한계점이 있다.

이러한 문제를 해결하기 위해 최근에는 딥러닝을 통해 자동으로 중요한 특징을 추출하고 모델을 학습하는 방법론이 제안되고 있다. 이러한 접근법들은 데이터로부터 HI를 추정하는데 있어, 대부분 지도 학습 모델을 활용한다(Roman et al., 2021). 예를 들어, Li et al.(2018)은 CNN을 사용하여 시스템의 잔여 수명을 추정하는 방법을 제안하였다. 이 방법은 복잡한 패턴을 학습하고 예측하는 데 뛰어난 성능을 보였다. 또 다른 HI 추정 접근법으로는 잔차 기반 접근법이 있다. 이 방법은 모델이 HI 레이블을 사용하여 시스템의 정상 동작을 인식하도록 학습한 후 재구성 오류를 분석하여 HI를 식별한다(de Pater and Mitici, 2023; Lövberg, 2021; Ye and Yu, 2021). 그러나 복잡한 기계 시스템의 경우, 레이블 데이터를 획득하기 위한 비용이 많이 들거나 산업적 특성으로 수집 자체가 불가능할 수 있다.

이러한 한계를 극복하기 위해 레이블이 없어도 학습이 가능한 비지도 학습 방법에 대한 관심이 점차 높아지고 있다(Bajarunas et al., 2024). 예를 들어, Malhotra et al.(2016)은 다중 센서 시계열 데이터를 사용하여 시스템의 건전성 지표를 얻기 위해 비지도 학습 기반의 long short term memory-based encoder-decoder 접근 방식을 제안하였다. 해당 방법론은 특정 열화 패턴을 가정하지 않아 다양한 기계와 상황에 적용 가능하다는 장점이 있다. Qin et al.(2021)은 VAE를 활용하여 비지도 학습 기반의 새로운 열화 추세 제약 방법을 제안하였으며, 이를 통해 보다 정확한 상태 예측이 가능함을 보여주었다. VAE를 통해 데이터의 숨겨진 구조를 학습하여 시스템의 상태를 평가하는 데 유용함을 보여주었다. Seitz et al.(2023)은 CNN 기반 비지도 autoencoder를 사용하여 초기 결함을 탐지하고, 측정 샘플에 자율적으로 레이블을 부여할 수 있는 학습 기법을 제안하였다.

위와 같은 비지도 학습 기반 방법론은 시스템 상태에 대한 레이블 없이 모니터링 데이터만을 통해 건전성 지표를 구축하기 때문에, 레이블 수집이 어려운 여러 산업 분야에 유용하다. 하지만 이러한 비지도 학습 방법론들도 기계 시스템이 처음 운용될 때부터 고장이 날 때까지의 생애 데이터를 필요로 하기 때문에 자동차와 같이 생애 주기가 긴 기계 시스템에 대해서는 적용하기가 어렵다. 이러한 이유로 현재 자동차와 관련된 건전성 지표 구축 연구는 배터리나 브레이크와 같은 특정 부품에 국한된 경우가 대부분이다(Alamelu Manghai and Jegadeeshwaran, 2019; Hu et al., 2020; Li et al., 2022).

3. 제안 방법론

3.1 데이터 수집 및 전처리

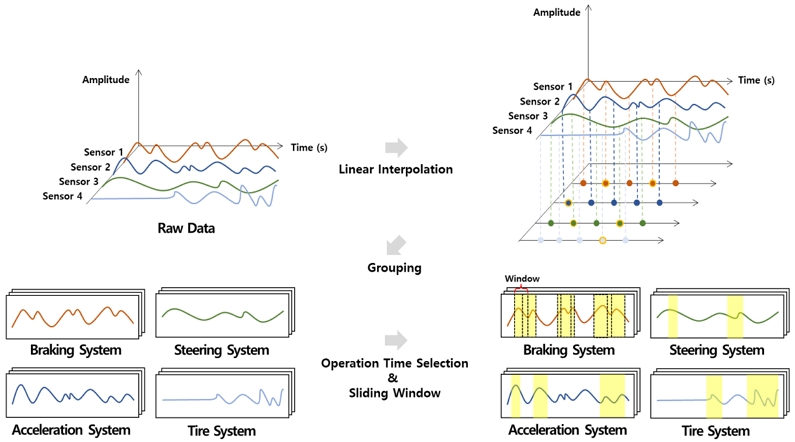
본 연구에서는 실제 차량을 운행하면서 225.2km부터 15,310.6km까지의 주행 데이터를 수집하여 건전성 지표를 구축하였다. 수집된 데이터는 모델링을 위해 <Figure 1>과 같은 전처리 과정을 거쳤다. 우선, 센서마다 샘플링 비율(sampling rate)이 다르며 특정 센서에서 결측치가 존재한다는 문제가 있었다. 이를 해결하기 위해 선형 보간법(linear interpolation)을 사용하여 541개의 센서 데이터의 샘플링 비율을 100Hz로 변환함과 동시에 결측치를 대체하였다. 이 때 샘플링 비율 100Hz는 각 센서 별 샘플링 비율의 최솟값과 최빈값이 0.01이라는 점에 근거하여 선정하였다. 또한, 차량의 여러 부품들은 생애 주기와 역할이 서로 다르다는 점을 고려하여, 부품들을 제동 시스템, 가속 시스템, 조향 시스템, 타이어 시스템으로 군집화하고, 도메인 지식을 기반으로 각 장치와 직/간접적으로 영향을 미치는 센서 데이터를 입력 변수로 선정하였다. 이를 통해 시스템별로 건전성 지표를 구축하고, 관리할 수 있는 기반을 마련하였다.

Figure 1.

The Process of Data Preprocessing

다음으로 각 시스템의 가동 유무를 알 수 있는 변수를 활용하여, 시스템이 작동하는 구간을 선정하였다. 예를 들어, 제동 시스템의 경우, 브레이크 실린더 압력을 이용해 제동 시스템의 가동 유무를 구분하고, 이를 기준으로 가동 구간을 선정하였다. 이때 차량 시동에서 브레이크가 사용되는 경우와 같이 변수 값은 시스템이 작동 중인 것으로 표시되지만, 실제로는 가동되지 않는 구간은 제외하였다. 또한, 주행 데이터 특성 상 노이즈가 많기 때문에, 가동 구간의 길이가 1초 미만인 경우는 노이즈로 간주하고 제외하였다. 마지막으로 입력 차원을 고정시키기 위해 시계열 데이터에서 일반적으로 많이 활용되는 슬라이딩 윈도우(sliding window) 기법을 적용하여 입력 샘플 $x m, n ∈ R v × w$ 을 구축하였다. 여기서 m은 특정 시스템에서 선정된 여러 가동 구간 중 m번째 가동 구간을 의미하며, n은 m 번째 가동 구간에 대해 슬라이딩 윈도우 기법을 적용해 생성된 여러 윈도우 중 n번째 윈도우를 의미한다. v와 w는 각각 특정 시스템에 대한 변수 개수와 윈도우 사이즈를 나타낸다.

3.2 LSTM-VAE를 활용한 차량 건전성 지표 개발

건전성 지표를 구축하는 기본적인 접근법은 특정 시점의 입력 모니터링 데이터 x와 해당 시점에서 기계 시스템의 상태를 측정한 출력 데이터 y의 관계를 학습하는 지도 학습을 활용하는 것이다. 그러나 자동차와 같이 복잡한 기계 시스템의 상태를 정확하게 측정하여 출력 데이터 y를 확보하는 것은 매우 어렵기 때문에, 상대적으로 수집하기 쉬운 입력 데이터 x만을 사용하는 비지도 학습 방법론이 주로 연구되고 있다. 비지도 학습 기반 방법론들은 일반적으로 기계 시스템 운용 시점마다 입력 데이터에서 중요한 특징 벡터를 추출하고, 이 특징 벡터 간 거리를 기반으로 건전성 지표를 구축한다. 하지만 이러한 접근법은 기계 시스템의 운용 초기부터 고장에 이르기까지의 생애 데이터를 필요로 하기 때문에, 운용 기간이 긴 차량 도메인에는 적합하지 않다. 본 연구에서는 LSTM-VAE(Bowman et al., 2015)를 활용하여 차량의 초기 생애 데이터만으로도 건전성 지표를 구축하는 방법을 제안한다.

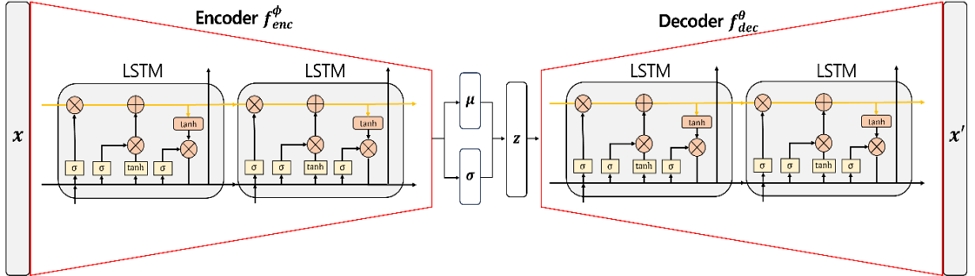
LSTM-VAE는 <Figure 2>처럼 VAE의 인코더(encoder)와 디코더(decoder)를 LSTM으로 구성하여 시계열 데이터 분포를 효과적으로 학습하고, 새로운 샘플을 생성하는 것을 목적으로 설계된 생성 모델의 일종이다. 먼저, 인코더는 입력 데이터 x로부터 입력 데이터의 특징을 잘 표현할 수 있는 저차원 특징 공간(feature space)의 분포를 학습하는 역할을 수행한다. 이 과정에서 특징 변수(feature variable)를 쉽게 제어하기 위해 특징 공간 분포를 다변량 가우시안 분포로 가정하며, 인코더는 다변량 가우시안 분포의 모수인 평균 벡터 μ와 표준 편차 σ를 추정한다. 디코더는 인코더에서 추정한 다변량 가우시안 분포에서 샘플링된 특징 변수 z를 입력 받아, 이를 다시 데이터 공간으로 복원하여 새로운 샘플을 생성하는 역할을 수행한다. 이를 위해 다음과 같은 손실 함수를 사용하여 모델을 학습시킨다.

a r g m i n ϕ, θ ∑ - E z ∼ q ϕ z x log p θ x z + λ D K L q ϕ z x p z

(1)

Figure 2.

The Architecture of LSTM-VAE

여기서 ϕ와 θ는 각각 LSTM으로 구성된 인코더와 디코더의 파라미터이다. D_KL(•)은 Kullback-Leibler(KL) divergence를 의미하며, λ는 KL-divergence 손실에 대한 가중치이다. 손실 함수의 첫 번째 항은 인코더로부터 추정된 잠재 공간의 사후 확률 분포 q_ϕ(z|x)에서 샘플링된 z가 주어졌을 때, 디코더에서 생성된 샘플이 입력 데이터일 가능도(likelihood) p_θ(x|z)를 최대화하도록 유도한다. 두 번째 항은 사후 확률 분포 q_ϕ(z|x)가 특징 변수의 사전 확률 분포 p(z)와 유사한 분포를 가지도록 규제하는 역할을 한다. 이 때, 모든 성분이 독립적이며 동일한 분산을 가져 샘플링과 관련된 연산이 매우 단순해진다는 정규 분포(0,)의 특성을 활용하여 사전 확률 분포 p(z)는 샘플링 조절에 용이하도록 정규 분포(0,)를 따른다고 가정한다. 위와 같은 학습 과정을 통해 LSTM-VAE는 복잡한 패턴을 가진 고차원 시계열 데이터를 가우시안 분포를 따르는 저차원 특징 공간으로 매핑 할 수 있게 된다. 이로 인해, 기존 데이터 공간에서는 측정하기 어려웠던 데이터 간 시계열 분포 변화를 잠재 벡터 간 거리 개념으로 측정할 수 있게 된다. 이러한 LSTM-VAE의 특성을 활용하여, 기존 VAE 계열 모델을 적용한 건전성 지표 구축 연구들은 기계 시스템의 노후화로 인한 분포 변화를 정량화하는 방법을 제안하였다(Gebraeel et al., 2005; Li et al., 2018; Orchard and Vachtsevanos, 2009). 그러나 이러한 접근법은 시스템의 모든 상태에 대한 특징 벡터가 충분히 학습된 경우에만 효과적으로 작동할 수 있다. 즉, VAE 기반의 기존 방법론들은 시스템의 모든 상태가 포함된 생애 전반에 걸친 모니터링 데이터를 필요로 하며, 이러한 조건은 생애 주기가 길어 데이터를 충분히 얻기 어려운 차량과 같은 기계 시스템에는 적용하기 어렵다는 한계가 있다.

본 연구에서는 VAE의 또 다른 특성을 활용하여 차량의 상태 변화를 측정하고, 건전성 지표를 구축하는 방법을 제안한다. 이 특성은 VAE 손실 함수인 Eq. 1의 첫 번째 항을 통해 유도된다. 먼저, 첫 번째 항인 E_z[log(p_θ(x|z))]를 계산하기 위해 몬테카를로 근사(Monte Carlo approximation)를 활용한다.

E z l o g p θ x z = ∫ l o g ⁡ p θ x z d z ≈ 1 / L ∑ l = 1 L l o g ⁡ p θ x z l

(2)

여기서 L은 근사를 위한 샘플링 횟수로 실제 학습 과정에서는 효율성을 위해 L = 1로 설정한다. 또한 p_θ(x|z^l)를 계산하기 위해서 디코더의 출력이 가우시안 분포를 따른다고 가정하면, 최종적으로 아래와 같은 관계를 유도할 수 있다.

E z l o g p θ x z ≈ l o g p θ x z = l o g 1 2 π e x p - x - x ′ 2 2 ∝ - x - x ′ 2

(3)

여기서 x는 입력 데이터이며, x^′은 인코더와 디코더를 거쳐서 재구축된 데이터이다. 즉, VAE는 손실 함수의 첫 번째 항을 최소화하기 위해 입력 데이터와 재구축된 데이터 간의 차이를 최소화하도록 학습된다. 이러한 손실 함수로 학습된 VAE는 학습 데이터와 유사한 분포를 가진 데이터가 입력되면 이를 적절한 특징 변수로 매핑하고, 입력 데이터와 유사한 재구축 데이터를 생성한다. 그러나 만약 학습 데이터와 다른 분포를 가진 데이터가 입력되면, VAE는 이를 적절한 잠재 변수로 변환하지 못하고 입력 데이터와는 다른 재구축 데이터를 생성하게 된다.

이러한 VAE의 특성은 재구축 오차를 통해 입력 데이터의 분포 변화를 정량화 할 수 있도록 도와준다. 본 연구에서는 차량에서 수집되는 센서 데이터의 분포가 노후화에 의해 변한다는 가정을 바탕으로, 차량의 노후화가 발생하지 않은 초기 주행 구간을 학습 데이터로 선정하고 LSTM-VAE를 학습시킨다. 이후 노후화가 진행되어 데이터 분포가 변하게 되면, VAE의 특성상 재구축 오차가 커지게 된다. 이 때, 건전성 지표는 다음과 같이 정의할 수 있다.

H I r e c o n i = e i = 1 N ∑ j = 1 N x i, j - x i, j ′ 22

(4)

여기서 i는 가동 구간 인덱스이며, N은 i번째 가동 구간에 존재하는 윈도우 개수를 의미한다. 즉, 건전성 지표 HI_recon(i)는 특정 시스템을 i번 사용했을 때 초기 주행 구간에 비해 얼마나 데이터 분포가 달라졌는지를 나타낸다.

3.3 누적합 기반 건전성 지표 개발

노후화로 인한 데이터 분포 변화는 보통 미세하게 변화하며, 차량 데이터 특성상 날씨와 환경으로 인한 노이즈가 많다. 이로 인해 단순히 재구축 오차만으로 건전성 지표를 구축할 경우, 높은 편차와 작은 평균 변화를 반영하지 못하고 신뢰할 수 있는 건전성 지표를 얻기 어려울 수 있다. 이러한 문제를 해결하기 위해서 본 연구에서는 누적합 관리도(Koshti, 2011) 개념을 도입한 누적합 기반 건전성 지표를 제안하였다.

누적합 관리도는 품질 관리에서 사용되는 통계적 도구 중 하나로, 공정이나 제품의 품질 변화를 추적하고 모니터링하는데 도움을 준다. 일반적인 관리도에서는 감시 통계량을 타점하여 데이터를 추적하지만, 이는 미세한 변화를 탐지하기 어렵다는 단점이 있다. 반면, 누적합 관리도는 여러 표본값의 목표값에 대한 편차의 누적합을 표시하기 때문에, 공정 평균이 조금만 달라져도 누적 편차 값이 크게 변화하여 미세한 변화를 감지하는데 효율적이다. 이러한 장점은 앞서 재구축 오차 기반 건전성 지표의 문제를 해결할 수 있는 특성으로, 본 연구에서는 이 개념을 활용하여 누적합 기반 건전성 지표를 구축하였다.

누적합 기반 건전성 지표를 계산하는 과정은 다음과 같다. 먼저, 초기 주행 구간에 대한 재구축 오차가 평균이 μ인 정규 분포를 따른다고 가정하고, 누적합 C₀는 0으로 초기 설정한다. 이 때, μ는 초기 주행 구간 중 검증 데이터를 따로 분리하여 아래와 같이 추정한다.

μ^= 1 M ∑ m = 1 M e m

(5)

여기서 M은 검증 데이터에 속한 가동 구간의 개수이다. 이후 새로운 가동 구간 i(M<i)에 대한 재구축 오차 e_i가 계산되면, 이를 검증 구간에 대한 재구축 오차 평균 $μ^$ 으로 표준화하며, 계산식은 아래와 같다.

z i = max e i - μ^- k, 0, if e i ≥ μ^min μ^- e i + k, 0, if e i < μ^

(6)

여기서 k는 공차 계수(tolerance factor)로, 재구축 오차의 허용 범위를 설정하는 하이퍼파라미터이다. 이후 누적합을 C_i = z_i + C_i_-1로 업데이트하며 이 과정을 반복하여 누적합을 갱신한다. 이러한 과정을 통해서 i번째 가동 구간에 대한 누적합 기반 건전성 지표 HI_cusum(i)를 계산할 수 있다.

H I c u s u m i = C i

(7)

누적합 기반 건전성 지표는 재구축 오차 기반 건전성 지표에서는 파악하기 어려운 미세한 분포 변화를 탐지하는 것에는 용이하지만, 부품 수리나 교체 등으로 분포가 정상화 될 경우, 즉각적인 반영이 어렵다는 한계점이 있다. 따라서 실제 활용 시 단순 재구축 기반 지표와 누적 기반 건전성 기반 지표를 상호 보완적으로 사용하는 것이 필요하다.

4. 실험 결과

4.1 실험 설정 및 정량적 평가지표

본 연구의 목적은 차량 초기 주행 데이터만을 활용하여 정량적인 건전성 지표를 구축하고, 이후 주행 데이터에서 발생하는 노후화 정도를 탐지하는 것이다. 이를 위해 본 연구에서는 전문가들의 도메인 지식을 기반으로 주행 거리 9,000km까지의 초기 주행 데이터를 학습 데이터로 사용하였다. 또한, 표본값의 목표값에 대한 편차를 누적합하기 위해 학습 / 검증 / 테스트 데이터를 주행 거리를 기준으로 0 ~ 7,500km / 7,500 ~ 9,000km / 9,000km ~ 로 분할하였다. 주행 데이터의 윈도우 사이즈는 100으로 설정하였고, 데이터 효율성 증가를 위해 학습 및 검증 데이터는 25% 간격으로 오버랩(overlap)을 두어 입력하였다. 테스트 데이터는 오버랩 없이 입력한 후 가동 구간 별 재구축 오차의 평균을 구하여 건전성 지표를 구축하였다.

<Table 1>은 LSTM-VAE 모델의 최적 하이퍼파라미터를 탐색하기 위한 조합을 나타낸다. 데이터 분포를 잘 학습한 모델을 찾기 위해 모델의 평균 재구축 오차가 가장 낮은 하이퍼파라미터를 탐색하였으며, <Figure 3>은 각 하이퍼파라미터 별 평균 재구축 오차의 분포를 시각화 한 결과이다. 이를 바탕으로 가장 낮은 재구축 오차를 반환하는 최적의 하이퍼파라미터 조합을 확인한 결과, 본 연구에서는 2개층의 LSTM 레이어를 가진 인코더와 디코더를 사용하였으며, 매개 변수 임베딩 벡터와 은닉층의 차원은 각각 128, 256로 설정하였다. KL divergence의 가중치 λ는 0.00025, 학습률은 0.001, 배치 사이즈(batch size)는 128, 에포크(epoch)는 150으로 설정하였으며, 옵티마이저(optimizer)는 Adam(Kingma and Ba, 2015)을 사용하였다. 누적합 기반 건전성 지표를 구축하는데 필요한 재구축 오차 평균 μ와 표준편차 σ는 검증 데이터를 통해 추정하였다.

Table 1.

Hyperparameter Search Space

Figure 3.

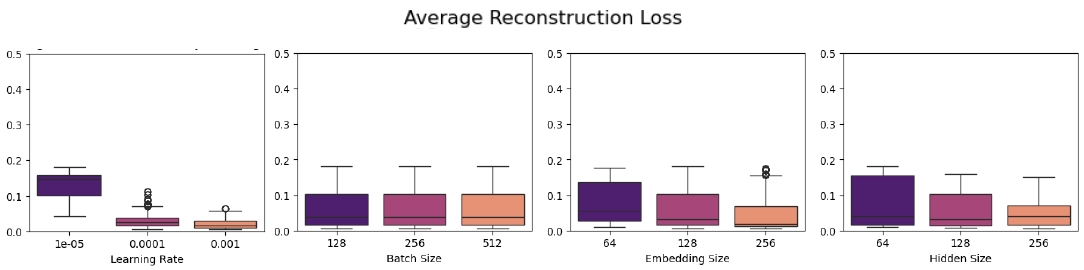
The Distribution of Average Reconstruction Loss for Different Hyperparameters(Learning Rate, Batch Size, Embedding Size, Hidden Size)

이와 함께, 공차 계수는 모든 시스템에 대해 동일하게 로 설정하였다. 이는 미세한 분포 변화를 신속하게 탐지하기 위해 선행 연구(Koshti, 2011; Lucas, 1985; Page, 1954)에서 널리 사용된 기준으로, 매우 작은 평균의 이동을 효과적으로 감지할 수 있도록 설정된 값이다. 특히, 누적합 관리도에서 해당 설정은 공정 이상이 발생한 시점부터 이를 감지하기까지 소요되는 관측값의 평균 개수인 평균 런 길이(average run length, ARL)를 최소화하며 공정의 민감도를 높이는데 유용한 값으로 일반적으로 사용된다. 따라서 본 연구에서도 이러한 기준을 따라 를 로 적용하여 모델의 노후화 탐지 성능을 최적화하였다.

시스템별 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표를 정량적으로 비교하기 위해 건전성 지표 평가에 널리 사용되는 robustness, trendability, monotonicity를 사용하였다(Bajarunas et al., 2024; Cheng et al., 2023; de Pater and Mitici, 2023; Hu et al., 2020; Qin et al., 2021). 각 평가지표는 K개의 가동 구간에 따른 특정 시스템의 건전성 지표를 HI={HI(i)}_i∈1:K라고 정의할 때, 아래와 같이 계산된다.

Robustness는 건전성 지표가 평균 추세 대비 얼마나 편차가 큰지 평가하는 지표이다. 이는 외부 환경 요인 및 노이즈에 의한 건전성 지표의 강건성을 나타내며, 다음 식으로 정의된다.

R o b H I = 1 K ∑ i = 1 K exp - H I i - H I i s H I i

(8)

여기서 HI(i)^s는 i번째 가동 구간에서의 이동 평균값을 의미한다. Eq. 8에서 지수 함수 내의 값은 i번째 가동 구간의 건전성 지표 HI(i)가 동일 시점의 이동 평균 HI(i)^s에서 얼마나 벗어나 있는지를 나타낸다. HI(i)와 HI(i)^s의 차이가 클수록 건전성 지표가 추세와 많이 멀어진 값을 가진다는 의미이며, 이는 지수 함수의 값을 0에 가깝게 만든다. 반대로 HI(i)와 HI(i)^s의 차이가 작다면, 현재 건전성 지표가 이동 평균과 유사한 값을 가진다는 의미로 큰 흐름의 변화가 없음을 나타낸다. 이 때, 지수 함수의 값은 1에 가까워진다.

Trendability는 가동 횟수와 건전성 지표 간 피어슨 상관계수(Pearson correlation coefficient)에 절대값을 취한 형태로 Eq. 9와 같이 계산된다.

T r e H I = K ∑ i = 1 K H I i i - ∑ i = 1 K H I i ∑ i = 1 K i (K ∑ i = 1 K H I i 2 - ∑ i = 1 K H I i 2) (K ∑ i = 1 K i 2 - ∑ i = 1 K i 2)

(9)

Trendability가 높다는 것은 가동 횟수 i와 이에 대응하는 건전성 지표 HI(i)가 선형적으로 큰 상관성이 을 가진다는 것을 나타내며, 이는 가동 횟수에 따라 증가하는 노후화의 특성을 건전성 지표가 잘 반영하고 있다는 것을 의미한다.

Monotonicity는 건전성 지표가 가동 횟수에 따라 일관되게 증가 혹은 감소하며, 변화나 역전이 발생하지 않아야 한다는 특성을 반영한 지표로 Eq. 10과 같이 정의된다.

M o n H I = 1 K - 1 ∑ i = 1 K I H I i + 1 > H I i - ∑ i = 1 K I H I i + 1 < H I i

(10)

여기서 I(•)는 함수(indicator function)로 괄호 안 조건을 만족하면 1, 만족하지 않으면 0을 반환한다. 따라서, 첫 번째 항은 i+1번째 가동 구간에서의 건전성 지표가 i번째 값보다 큰, 즉 건전성 지표가 증가한 횟수를 나타내며, 두 번째 항은 건전성 지표가 이전 값보다 감소한 횟수를 나타낸다. 즉, monotonicity가 높다는 것은 건전성 지표가 일정한 방향으로 변화함을 의미하며, 값이 높을수록 단조성이 강한 건전성 지표임을 나타낸다. 위 세 가지 평가지표는 모두 0과 1사이의 값으로 나타내며, 각 지표의 값이 높을수록 해당 건전성 지표가 기계 시스템의 노후화를 잘 나타냄을 의미한다.

4.2 시스템별 건전성 지표 정량적 평가

<Table 2>는 시스템별로 계산된 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표에 대한 정량적 평가를 나타낸다. 먼저, 재구축 오차 기반 건전성 지표는 모든 시스템에 대해 0.5에서 0.8사이의 비교적 낮은 robustness를 보였다. 이는 초기 주행 데이터로 학습한 모델이 차량 시스템의 노후화와 관련이 없는, 학습 환경에서 보지 못했던 도로 환경 및 날씨 등과 같은 노이즈에 의한 분포 변화에 강건하게 대응하지 못했음을 의미한다. 이러한 낮은 robustness는 건전성 지표의 변동성을 높이고 일관성을 떨어뜨려, 지표에 대한 해석을 어렵게 만드는 원인이 된다. 반면, 누적합 기반 건전성 지표는 모든 시스템에서 0.97 이상의 매우 높은 robustness를 달성하였다. 이는 누적합 기반 건전성 지표가 외부적인 주행 환경 변화로 인한 노이즈에 대해 강건함을 보여주며, 단순 재구축 오차 기반 건전성 지표의 한계점을 보완함을 의미한다.

Table 2.

Comparison Results of HIs for Three Evaluation Metrics of Tire, Braking, Steering, and Acceleration Systems. The Experiments Were Repeated Five Times with Different Seeds

재구축 오차 기반 건전성 지표는 모든 시스템에 대해 낮은 trendability를 보였으며, 특히 타이어 시스템을 제외한 다른 시스템에서는 0.1 이하의 매우 낮은 값을 기록하였다. 이는 재구축 오차 기반 건전성 지표가 가동 횟수에 따라서 미세하게 변화하는 데이터 분포를 제대로 반영하지 못한다는 것을 의미한다. 반면, 누적합 기반 건전성 지표는 모든 시스템에 대해서 0.95 이상의 높은 trendability를 달성하였으며, 이는 재구축 오차 기반 건전성 지표가 탐지하지 못하는 미세한 데이터 분포 변화를 잘 반영하고 있음을 보여준다. 특히 제동 시스템과 타이어 시스템의 경우 타이어 공기압 주입, 브레이크 패드 교체와 같은 유지보수 작업으로 인해 시스템의 노후화가 개선되는 상황이 존재하기 때문에, 조향 시스템이나 가속 시스템에 비해서 이들 시스템의 trendability가 다소 낮게 나타났다.

건전성 지표 추세의 일관성을 대변하는 monotonicity의 경우, 누적합 기반 건전성 지표에서 일부 개선이 이루어지긴 했지만, 여전히 0.07에서 0.23으로 낮은 성능을 보이고 있다. 이는 누적합 기반 건전성 지표가 노이즈로 인한 재구축 오차의 변동성을 줄일 수는 있지만, 그 변동성을 완전히 제거하고 건전성 지표가 일관되게 증가하도록 만들지는 못한다는 것을 보여준다. 또한, monotonicity는 기계 시스템의 대한 노후화가 단조 증가한다는 가정을 기반으로 하지만, 실제로는 부품 수리나 교체로 인해 노후화가 개선되는 상황이 존재한다. 이러한 이유로 monotonicity 지표만으로는 건전성 지표의 일관성을 완전히 평가하기 어려울 수 있다. 따라서 정량적 평가 지표 뿐만 아니라, 시스템 교체에 따른 건전성 지표 추세 변화를 확인하기 위해 시각화를 통한 정성적 평가도 병행할 필요가 있다.

4.3 시스템별 건전성 지표 정성적 평가

본 장에서는 네 개의 시스템에 대한 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표를 정성적으로 비교하였다. <Figure 4>는 타이어 시스템에 대한 건전성 지표를 시각화한 것으로, 왼쪽과 오른쪽은 각각 테스트 데이터에 대한 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표를 나타낸다. 이 때 점선은 공기압 보충 및 타이어 교체와 같은 장비 유지 보수 이벤트 시점을 나타내며 해당 시점은 노후화의 개선이 일어나 건전성 지표의 하락 가능성이 있는 시점을 의미한다. 또한 해당 그래프의 아래쪽 x 레이블은 데이터 전처리 과정에서 설정한 시스템 별 가동구간 인덱스를 나타내고, 위쪽 x 레이블은 해당 인덱스에 상응하는 차량의 누적 주행 거리(odometer)를 의미한다.

Figure 4.

Visualization of the Tire System HI with Maintenance Events. x- and y-axes Represent an Operational Time Index, Odometer and a Health Indicator

<Figure 4>의 왼쪽에 있는 재구축 오차 기반 건전성 지표는 부품 교체 시 건전성 지표가 즉각적으로 감소한 후, 점차 다시 증가하는 패턴을 보인다. 이는 부품 상태가 개선됨에 따라 노후화 가 개선되었음을 잘 나타내지만, 그로 인해 건전성 지표 자체의 변동성이 크다는 한계점을 확인할 수 있었다. 반면, <Figure 4>의 오른쪽에서 보여주는 누적합 기반 건전성 지표는 외부 요소에 의해 발생하는 변동성이 적고, 가동 횟수에 따라 점차 증가하는 우상향 추세를 보인다. 이는 누적합 기반 건전성 지표가 재구축 오차의 변동성을 줄일 수 있음을 보여준다. 다만, 누적합 특성상 노후화 개선 상황을 탐지할 수는 있지만, 지표가 즉각적으로 낮아지지 않고 서서히 줄어드는 경향성이 나타난다. 이러한 결과는 두 지표를 모두 활용하는 것이 차량 시스템의 노후화 상태를 보다 정확하게 진단하는데 효과적임을 보여준다.

또한 타이어 공기압 보충 이벤트에는 건전성 지표의 변화가 상대적으로 미미하지만, 타이어 완전 교체 시에는 두 건전성 지표에서 모두 큰 감소폭이 나타난 것을 볼 수 있다. 이는 타이어 교체가 타이어 공기압 주입보다 노후화 개선에 더 큰 영향을 미친다는 점을 고려할 때, 적절한 유지 보수 계획을 수립하는 데 있어 두 건전성 지표를 함께 사용하는 것이 중요함을 보여준다. 이와 같이, 본 연구는 단순 재구축 오차 기반 건전성 지표와 누적합 기반 건전성 지표의 상호 보완적 활용이 차량 시스템의 상태 진단과 유지보수 전략 수립에 있어 보다 정확하고 신뢰할 수 있는 평가를 제공할 수 있음을 강조한다.

<Figure 5>는 제동 시스템에 대한 재구축 오차 기반 건전성 지표(왼쪽)와 누적합 기반 건전성 지표(오른쪽)를 시각화한 그래프이다. 점선으로 표시된 부분은 브레이크 오일 교체 및 브레이크 패드 교체 시점을 나타낸다. 먼저, 재구축 오차 기반 건전성 지표를 살펴보면, 타이어 시스템과 달리 명확한 증가 추세를 찾을 수 없으며, 노이즈로 인한 변동성 때문에 제동 시스템의 상태를 일관되게 평가하기 어렵다는 것을 확인할 수 있다. 반면, 누적합 기반 건전성 지표에서는 명확한 우상향 추세를 확인할 수 있다. 이는 누적합 기반 건전성 지표가 재구축 오차만으로는 탐지하기 어려운 미세한 데이터 분포 변화를 탐지할 수 있음을 보여준다. 주목할 점은, 제동 시스템과 관련된 부품을 교체하는 상황에서는 타이어 시스템과 달리 건전성 지표의 감소 패턴이 두드러지지 않는다는 것이다. 이는 LSTM-VAE 모델이 제동 시스템과 관련된 부품의 보수 및 교체에 따른 주행 데이터의 변화를 잘 포착하지 못했다는 것을 의미한다. 하지만, 일반적으로 브레이크 패드와 브레이크 오일의 권장 교체 주기가 약 30,000km에서 40,000km 이상인 점을 고려했을 때, 본 연구에 사용한 15,000km 이하의 주행 데이터 상에서는 해당 부품들의 노후화 정도가 시스템의 성능 저하를 가져 올만큼 심하지 않아 데이터의 분포 변화가 두드러지지 않은 상황으로도 해석할 수 있다.

Figure 5.

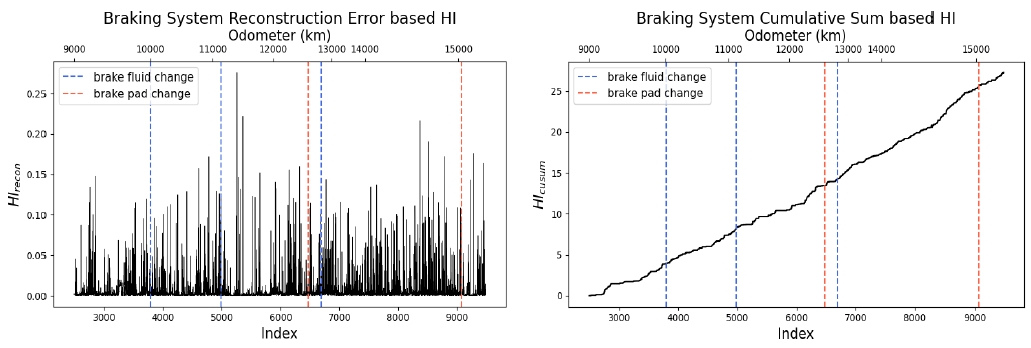
Visualization of the Braking System HI with Maintenance Events. x- and y-axes Represent an Operational Time Index, Odometer and a Health Indicator

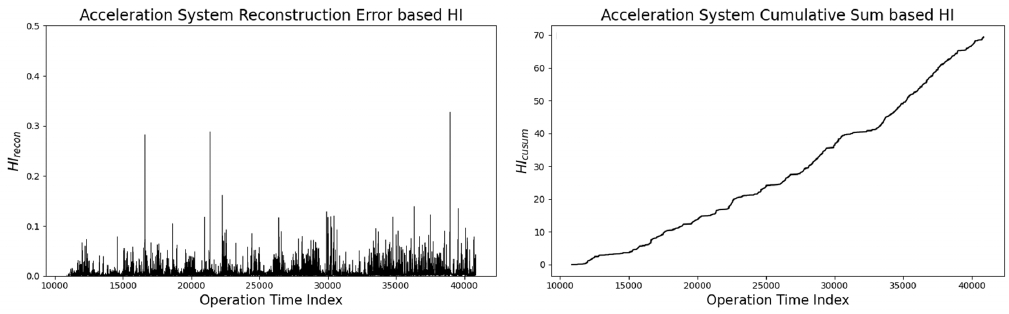
<Figure 6>과 <Figure 7>은 각각 조향 시스템과 가속 시스템의 재구축 기반 건전성 지표와 누적합 기반 건전성 지표를 나타낸다. 이 두 시스템은 타이어 및 제동 시스템과 다르게 관련 부품의 유지 보수 이벤트가 발생하지 않았기 때문에 이론적으로는 시스템의 노후화가 가동 횟수에 따라 증가해야 한다. 그러나 두 시스템 모두에서 단순 재구축 기반 건전성 지표는 시스템의 노후화를 잘 포착하지 못한 것을 볼 수 있다. 이는 차량의 가속 페달, 스티어링 휠(steering wheel)과 같은 장치는 차량 생애 전반에 걸쳐 미세하게 노후화되며, 이를 측정하는 센서의 데이터 변동 역시 매우 작은 작기 때문에 재구축 오차 기반 지표로는 이러한 변화를 감지하기 어렵다는 것을 보여준다. 반면, 누적합 기반 건전성 지표는 가동 횟수에 따라 진행되는 시스템의 노후화를 명확하게 포착하였다. 이는 시스템의 상태 변화를 누적된 데이터 변화를 통해 감지함으로써, 단순 재구축 오차 기반 지표의 한계점을 보완하고, 시스템 상태 변화를 더 신뢰성 있게 반영할 수 있음을 보여준다.

Figure 6.

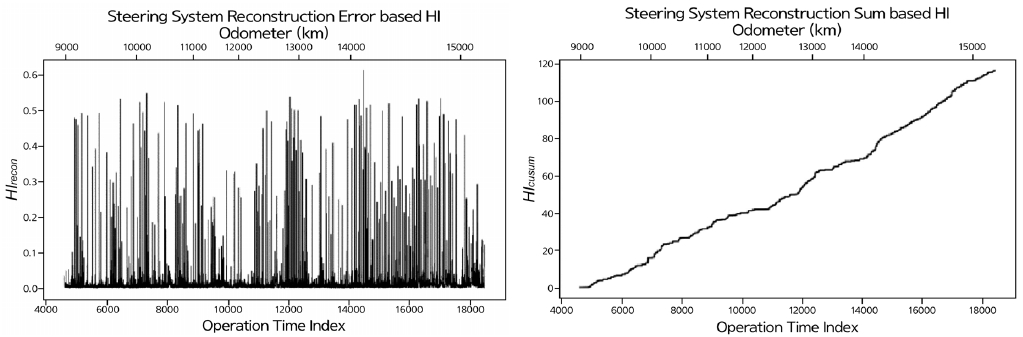
Visualization of the Steering System HI with Maintenance Events. x- and y-axes Represent an Operational Time Index, Odometer and a Health Indicator

Figure 7.

Visualization of the Acceleration System HI with Maintenance Events. x- and y-axes Represent an Operational Time Index, Odometer and a Health Indicator, Respectively

4.4 백본 모델 및 재구축 오차 기반 알고리즘 비교

본 장에서는 제안된 누적합 기반 건전성 지표의 타당성을 검증하기 위해 두 가지 추가 분석을 수행하였다. 먼저, VAE 모델의 구조 적합성을 평가하기 위해 백본(backbone) 모델을 변경하여 노후화 지표의 성능 변화를 평가했으며, 다음으로는 VAE가 아닌 다른 최신 재구축 오차 기반 알고리즘과의 비교를 통해 지표의 고도화 가능성을 검토하였다. 해당 분석은 4.1절에서 정의한 robustness, trendability, monotonicity의 세 가지 평가 지표를 활용하여 정량적 비교를 수행하였다.

<Table 3>은 VAE 모델의 백본 구조를 LSTM, 1D-CNN(Kim, 2014), transformer(Vaswani et al., 2017) 로 설정하여 각 시스템에서의 성능을 정량적으로 평가한 결과를 나타낸다. 실험 결과, 모든 백본 모델에서 누적합 기반 건전성 지표가 재구축 오차 기반 건전성 지표보다 우수한 성능을 나타내는 것을 확인할 수 있었다. 특히, 누적합 기반 건전성 지표는 robustness와 trendability 측면에서 모든 백본 모델과 시스템에서 0.95 이상의 높은 성능을 일관되게 유지하며, 차량 주행 데이터의 노이즈와 분포 변화에도 강건한 특징을 나타냈다. 또한, 누적합 기반 건전성 지표는 각 시스템에서 백본 모델 간의 성능 차이가 0.05 이하로 나타났으며, 이는 모델 구조의 차이에 관계없이 안정적이고 일관된 높은 성능을 유지함을 의미한다. 이러한 결과는 누적합 기반 건전성 지표가 차량의 노후화에 따른 분포 변화를 효과적으로 포착하며, 다양한 모델 구조에서도 강건하게 노후화를 대변하여 높은 신뢰성을 제공할 수 있음을 시사한다.

Table 3.

Comparison Results of HIs for Three Evaluation Metrics for Various Backbone Models of Tire, Braking, Steering, and Acceleration Systems. The Experiments were Repeated Five Times with Different Seeds

다음으로 제안하는 방법론의 고도화 가능성을 검증하기 위해 최신 재구축 오차 기반 방법론인 USAD(unsupervised anomaly detection)(Audibert et al., 2020)와 anomaly transformer(Xu et al., 2021)를 활용하여 건전성 지표의 성능을 비교하였다. USAD는 autoencoder와 GAN(Goodfellow et al., 2014)을 결합한 알고리즘으로, 정상 데이터의 분포를 학습한 후 비정상 데이터가 입력되었을 때 재구축 오차를 측정하여 이상치를 탐지한다. 이 알고리즘은 GAN의 구조를 활용하여, 학습된 정상 데이터와 비정상 데이터 간의 분포 차이를 증폭시키는 데 강점을 가진다. Anomaly transformer는 시계열 데이터의 정상 패턴을 학습하기 위해 transformer 아키텍처를 기반으로 설계되었으며, 정상 데이터와 비정상 데이터 간의 미세한 차이를 탐지하기 위해 association discrepancy라는 개념을 도입하였다. 이 알고리즘은 두 가지 상관성(association)을 학습하는데, prior association은 시계열 데이터의 전반적 분포를 반영하며, series association은 시계열 데이터 내에서 시간적 관계를 모델링하여 각 시점에서의 정상적 상관성을 학습한다. 그리고 이러한 두 상관성 간의 차이를 나타내는 association discrepancy를 통해 정상 데이터와 비정상 데이터 간의 세밀한 차이를 효과적으로 학습한다. 해당 두 알고리즘은 모두 정상 데이터의 분포를 학습하고 비정상 데이터가 입력되었을 때 학습되지 않은 데이터 분포로 인한 차이를 기반으로 이상치를 탐지한다는 점에서, 제안하는 누적합 기반 건전성 지표의 작동 원리와 유사하다. 다시 말해, 초기 주행 데이터를 학습하여 노후화 이전 데이터의 분포를 모델링 한 뒤, 이후 재구축 오차를 반환하는 방식으로 동작한다는 공통점을 바탕으로, 제안하는 누적합 기반 건전성 지표 구축 프로세스를 USAD 및 anomaly transformer 모델과 결합하여 성능을 비교하였다. <Table 4>는 제안 방법론, USAD, anomaly transformer를 활용하여, 각 차량 시스템에 대해 구축한 건전성 지표의 성능을 비교한 실험 결과를 나타낸다.

Table 4.

Comparison Results of HIs for Three Evaluation Metrics for Various Reconstruction Error based Algorithms of Tire, Braking, Steering, and Acceleration Systems. The Experiments were Repeated Five Times with Different Seeds

세 가지 알고리즘을 사용한 비교 실험 결과, 단순히 재구축 오차를 사용하는 경우에는 모든 모델에서 trendability와 monotonicity가 거의 0에 가까운 값을 보여, 효과적인 건전성 지표로 활용하기에는 한계가 있음을 확인할 수 있었다. 반면, 제안하는 누적합 기반 건전성 지표 구축 프로세스를 적용했을 때, 모든 모델이 세 가지 평가 지표에서 현저한 개선을 이루었다. 이는 제안하는 프로세스가 차량 주행 데이터의 높은 노이즈와 미세한 분포 변화를 효과적으로 반영함을 입증한다. 특히, 특정 시스템에서 낮은 성능을 보이는 USAD와 달리, LSTM-VAE와 anomaly transformer는 모든 시스템에서 준수한 성능을 보여주었다. 이는 USAD가 MLP(multi-layer perceptron) 기반의 구조로 설계되어 시계열 데이터의 시간적 의존성을 효과적으로 학습하지 못하기 때문으로 분석된다. MLP는 입력 데이터를 독립적으로 처리하기 때문에 시간 순서에 따른 패턴이나 변화 학습에 한계가 있으며, 이러한 구조적 특성으로 인해 trendability와 monotonicity 측면에서 낮은 성능을 보인다.

반면, LSTM-VAE와 anomaly transformer는 각각 LSTM과 transformer 기반의 구조를 활용하여 시계열 데이터의 특성을 효과적으로 학습한다. 이러한 구조적 강점 덕분에 LSTM-VAE와 anomaly transformer는 차량 주행 데이터의 미세한 분포 변화를 안정적으로 반영하여 모든 시스템에 대해 일관된 성능 향상을 나타냈다. 이는 시계열적 특징을 반영하는 재구축 알고리즘을 활용할 경우, 누적합 기반 건전성 지표 구축 프로세스는 더욱 효과적으로 작동하며, 차량 데이터의 노후화와 미세한 분포 변화를 정밀하게 반영할 수 있음을 입증한다.

5. 결 론

차량과 같이 생애 주기가 길고 복잡한 기계 시스템은 기존의 건전성 지표 구축 방법론을 적용하기 어렵다. 본 연구에서는 이러한 문제를 해결하기 위해서 LSTM-VAE의 특성을 활용하여 초기 생애 데이터만으로 건전성 지표를 구축하는 방법론을 제안하였다. 구체적으로, 노후화가 진행됨에 따라 차량에서 수집되는 데이터 분포가 변화한다는 가설 하에 노후화가 일어나지 않았다고 볼 수 있는 초기 생애 데이터만으로 LSTM-VAE를 학습하고, 이후 노후화로 인한 분포 변화를 재구축 오차로 측정하는 건전성 지표를 설계하였다. 그러나, 재구축 오차 기반 건전성 지표는 차량 주행 데이터의 미세한 변화를 충분히 탐지하지 못했으며, 차량 시스템의 가동 횟수에 따른 노후화보다는 외부 요인에 의한 변동성이 크다는 한계가 있었다. 이를 해결하기 위해 누적합 관리도 개념을 활용하여 누적합 기반 건전성 지표를 제안하였고 해당 방법론이 건전성 지표에 적합하다는 것을 실제 차량 주행 데이터를 통해 실험적으로 확인하였다. 본 연구는 생애 데이터를 충분히 확보하기 어려운 상황에서도 효과적인 건전성 지표 구축의 가능성을 제시하였다. 이를 통해 차량 상태 변화를 효과적으로 감지함으로써, 향후 차량 및 기계 시스템의 유지보수 시점이나 부품 교체 주기를 결정하는 등 전체 생애 주기가 길어 건전성 지표 구축이 어려운 다양한 산업에서도 상태 모니터링과 유지보수 전략 수립에 새로운 방향성을 제공할 수 있을 것으로 기대된다. 또한, 이러한 건전성 지표를 활용하면 차량 운행 안전성을 높이고 운전자의 안전을 증진시켜, 궁극적으로 자동차 제조사와 운송 업체의 운영 효율과 경쟁력을 향상시키는 데 기여할 수 있을 것으로 기대된다.

본 연구는 단일 차량의 초기 약 13,000km 주행 데이터만을 사용하여 진행되었다. 해당 데이터에는 각 시스템 별 성능 개선이 필요한 이벤트들이 포함되어 있으나, 여전히 다양한 주행 시나리오를 충분히 반영하지 못한다는 한계가 있다. 이러한 한계로 인해 제안하는 모델이 건전성 지표의 감소를 충분히 반영하지 못하는 결과를 초래하였다. 또한, 본 연구에서 제안하는 누적합 기반 노후화 지표는 차량의 노후화 진행 상황을 제시할 수는 있으나, 해당 건전성 지표의 절대적인 값을 통해 차량의 노후화 진행 정도를 정량적으로 평가하는 데는 한계가 있다. 이를 보완하기 위해, 향후 연구에서는 제안된 건전성 지표를 기반으로 다양한 주행 데이터를 추가로 수집하고, 이를 활용한 잔존 수명 예측 프로세스를 개발할 계획이다. 특히, 다양한 시점에서 발생한 이벤트를 포함한 추가 데이터를 활용한다면, 현재 구축한 누적합 기반 건전성 지표의 타당성을 검증하고 연구 방법론의 일반화가 가능할 것이라 기대한다.

Acknowledgments

This research was supported by Hyundai Mobis and BK21 FOUR.

References

Ahmadzadeh, F. and Lundberg, J. (2014), Remaining useful life estimation, International Journal of System Assurance Engineering and Management, 5, 461-474. [https://doi.org/10.1007/s13198-013-0195-0]
Alamelu Manghai, T. M. and Jegadeeshwaran, R. (2019), Vibration based brake health monitoring using wavelet features: A machine learning approach, JVC/Journal of Vibration and Control, 25(18) [https://doi.org/10.1177/1077546319859704]
Bajarunas, K., Baptista, M. L., Goebel, K., and Chao, M. A. (2024), Health index estimation through integration of general knowledge with unsupervised learning, Reliability Engineering & System Safety, 110352. [https://doi.org/10.1016/j.ress.2024.110352]
Bhatti, G., Mohan, H., and Singh, R. R. (2021), Towards the future of smart electric vehicles: Digital twin technology, Renewable and Sustainable Energy Reviews, 141, 110801. [https://doi.org/10.1016/j.rser.2021.110801]
Bowman, S. R., Vilnis, L., Vinyals, O., Dai, A. M., Jozefowicz, R., and Bengio, S. (2015), Generating sentences from a continuous space, ArXiv Preprint ArXiv:1511.06349, . [https://doi.org/10.18653/v1/K16-1002]
Byington, C. S., Watson, M., Edwards, D., and Stoelting, P. (2004), A model-based approach to prognostics and health management for flight control actuators, IEEE Aerospace Conference Proceedings, 6 [https://doi.org/10.1109/AERO.2004.1368172]
Cheng, G., Lau, S., Tam, N., Wu, Z., Hu, A., Law, Y. N., Lai, E., and Ge, M. (2023), Unsupervised Remaining Useful Life Prediction for Bearings with Virtual Health Index, 2023 13th International Conference on Power, Energy and Electrical Engineering, CPEEE 2023 [https://doi.org/10.1109/CPEEE56777.2023.10217714]
Daigle, M. J. and Goebel, K. (2013), Model-based prognostics with concurrent damage progression processes, IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 43(3) [https://doi.org/10.1109/TSMCA.2012.2207109]
de Pater, I. and Mitici, M. (2023), Developing health indicators and RUL prognostics for systems with few failure instances and varying operating conditions using a LSTM autoencoder, Engineering Applications of Artificial Intelligence, 117 [https://doi.org/10.1016/j.engappai.2022.105582]
Gao, Z., Ding, S. X., and Cecati, C. (2015), Real-time fault diagnosis and fault-tolerant control, IEEE Transactions on Industrial Electronics, 62(6), 3752-3756. [https://doi.org/10.1109/TIE.2015.2417511]
Gebraeel, N. Z., Lawley, M. A., Li, R., and Ryan, J. K. (2005), Residual-life distributions from component degradation signals: A Bayesian approach, IIE Transactions (Institute of Industrial Engineers), 37(6) [https://doi.org/10.1080/07408170590929018]
Ghimire, R., Sankavaram, C., Ghahari, A., Pattipati, K., Ghoneim, Y., Howell, M., and Salman, M. (2011), Integrated model-based and data-driven fault detection and diagnosis approach for an automotive electric power steering system, Autotestcon (Proceedings) [https://doi.org/10.1109/AUTEST.2011.6058760]
Hu, X., Che, Y., Lin, X., and Deng, Z. (2020), Health Prognosis for Electric Vehicle Battery Packs: A Data-Driven Approach, IEEE/ASME Transactions on Mechatronics, 25(6) [https://doi.org/10.1109/TMECH.2020.2986364]
Jia, X., Huang, B., Feng, J., Cai, H., and Lee, J. (2018), Review of PHM data competitions from 2008 to 2017: Methodologies and analytics, Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM. [https://doi.org/10.36001/phmconf.2018.v10i1.462]
Kingma, D. P. and Ba, J. L. (2015), Adam: A method for stochastic optimization, 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings.
Koshti, V. V. (2011), Cumulative sum control chart, International Journal of Physics and Mathematical Sciences, 1(1), 28-32.
Li, A., Yang, X., Dong, H., Xie, Z., and Yang, C. (2018), Machine learning-based sensor data modeling methods for power transformer PHM, Sensors (Switzerland), 18(12) [https://doi.org/10.3390/s18124430]
Li, R., Hong, J., Zhang, H., and Chen, X. (2022), Data-driven battery state of health estimation based on interval capacity for real-world electric vehicles, Energy, 257 [https://doi.org/10.1016/j.energy.2022.124771]
Li, X., Ding, Q., and Sun, J. Q. (2018), Remaining useful life estimation in prognostics using deep convolution neural networks, Reliability Engineering and System Safety, 172 [https://doi.org/10.1016/j.ress.2017.11.021]
Lövberg, A. (2021), Remaining Useful Life Prediction of Aircraft Engines with Variable Length Input Sequences, Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM, 13(1) [https://doi.org/10.36001/phmconf.2021.v13i1.3108]
Luo, J., Namburu, M., Pattipati, K. R., Qiao, L., and Chigusa, S. (2010), Integrated model-based and data-driven diagnosis of automotive antilock braking systems, IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 40(2) [https://doi.org/10.1109/TSMCA.2009.2034481]
Malhotra, P., Tv, V., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., and Shroff, G. (2016), Multi-sensor prognostics using an unsupervised health index based on LSTM encoder-decoder, ArXiv Preprint ArXiv:1608.06154, .
Montgomery, D. C. (2019), Introduction to statistical quality control, John Wiley & Sons.
Orchard, M. E. and Vachtsevanos, G. J. (2009), A particle-filtering approach for on-line fault diagnosis and failure prognosis, Transactions of the Institute of Measurement and Control, 31(3-4) [https://doi.org/10.1177/0142331208092026]
Qin, Y., Zhou, J., and Chen, D. (2021), Unsupervised health indicator construction by a novel degradation-trend-constrained variational autoencoder and its applications, IEEE/ASME Transactions on Mechatronics, 27(3), 1447-1456. [https://doi.org/10.1109/TMECH.2021.3098737]
Ranasinghe, K., Sabatini, R., Gardi, A., Bijjahalli, S., Kapoor, R., Fahey, T., and Thangavel, K. (2022), Advances in Integrated System Health Management for mission-essential and safety-critical aerospace applications, Progress in Aerospace Sciences, 128, 100758. [https://doi.org/10.1016/j.paerosci.2021.100758]
Rezaeianjouybari, B. and Shang, Y. (2020), Deep learning for prognostics and health management: State of the art, challenges, and opportunities, Measurement, 163, 107929. [https://doi.org/10.1016/j.measurement.2020.107929]
Roman, D., Saxena, S., Robu, V., Pecht, M., and Flynn, D. (2021), Machine learning pipeline for battery state-of-health estimation, Nature Machine Intelligence, 3(5) [https://doi.org/10.1038/s42256-021-00312-3]
Sankavaram, C., Pattipati, B., Pattipati, K., Zhang, Y., Howell, M., and Salman, M. (2012), Data-driven fault diagnosis in a hybrid electric vehicle regenerative braking system, IEEE Aerospace Conference Proceedings [https://doi.org/10.1109/AERO.2012.6187368]
Seitz, S., Arnold, M., Tetzlaff, R., and Holstein, P. (2023), Self-Supervised Health Index Curve Generation for Condition-Based Predictive Maintenance, Electronics (Switzerland), 12(24) [https://doi.org/10.3390/electronics12244941]
Tang, Y., Zhao, L., Zhang, S., Gong, C., Li, G., and Yang, J. (2020), Integrating prediction and reconstruction for anomaly detection, Pattern Recognition Letters, 129, 123-130. [https://doi.org/10.1016/j.patrec.2019.11.024]
Wang, M. H., Chao, K. H., Sung, W. T., and Huang, G. J. (2010), Using ENN-1 for fault recognition of automotive engine, Expert Systems with Applications, 37(4) [https://doi.org/10.1016/j.eswa.2009.09.041]
Xu, J., Wang, Y., and Xu, L. (2013), PHM-oriented integrated fusion prognostics for aircraft engines based on sensor data, IEEE Sensors Journal, 14(4), 1124-1132. [https://doi.org/10.1109/JSEN.2013.2293517]
Xu, J., Wu, H., Wang, J., and Long, M. (2022), Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy, ICLR 2022 - 10th International Conference on Learning Representations.
Ye, Z. and Yu, J. (2021), Health condition monitoring of machines based on long short-term memory convolutional autoencoder, Applied Soft Computing, 107 [https://doi.org/10.1016/j.asoc.2021.107379]
Yu, W., Kim, I. Y., and Mechefske, C. (2019), Remaining useful life estimation using a bidirectional recurrent neural network based autoencoder scheme, Mechanical Systems and Signal Processing, 129 [https://doi.org/10.1016/j.ymssp.2019.05.005]
Zhang, L., Lin, J., Liu, B., Zhang, Z., Yan, X., and Wei, M. (2019), A review on deep learning applications in prognostics and health management, IEEE Access, 7, 162415-162438. [https://doi.org/10.1109/ACCESS.2019.2950985]
Audibert, J., Michiardi, P., Guyard, F., Marti, S., and Zuluaga, M. A. (2020), USAD: UnSupervised Anomaly Detection on Multivariate Time Series, Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 3395-3404 [https://doi.org/10.1145/3394486.3403392]
Bowman, S. R., Vilnis, L., Vinyals, O., Dai, A. M., Jozefowicz, R., and Bengio, S. (2015), Generating sentences from a continuous space, ArXiv Preprint ArXiv:1511.06349, . [https://doi.org/10.18653/v1/K16-1002]
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014), Generative Adversarial Networks, http://arxiv.org/abs/1406.2661, .
Jalayer, M., Orsenigo, C., and Vercellis, C. (2021), Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, Fast Fourier and continuous wavelet transforms, Computers in Industry, 125 [https://doi.org/10.1016/j.compind.2020.103378]
Kim, Y. (2014), Convolutional Neural Networks for Sentence Classification, http://arxiv.org/abs/1408.5882, . [https://doi.org/10.3115/v1/D14-1181]
Kingma, D. P. and Welling, M. (2013), Auto-Encoding Variational Bayes, http://arxiv.org/abs/1312.6114, .
Oh, Y. K., Yoon, K., Park, J., and Kim, S. (2024), Comparative evaluation of VAE-based monitoring statistics for real-time anomaly detection in AIS data, Maritime Policy and Management [https://doi.org/10.1080/03088839.2024.2388177]
Qian, J., Song, Z., Yao, Y., Zhu, Z., and Zhang, X. (2022), A review on autoencoder based representation learning for fault detection and diagnosis in industrial processes, In Chemometrics and Intelligent Laboratory Systems, 231, Elsevier B.V. [https://doi.org/10.1016/j.chemolab.2022.104711]
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. (2017), Attention Is All You Need. http://arxiv.org/abs/1706.03762, .
Xu, J., Wu, H., Wang, J., and Long, M. (2021), Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy, http://arxiv.org/abs/2110.02642, .
Lucas, J. M. (1985), Counted Data CUSUM’s (Vol. 27, Issue 2). [https://doi.org/10.2307/1268761]
Page, E. S. (1954), Continuous Inspection Schemes (Vol. 41, Issue 1), https://about.jstor.org/terms, . [https://doi.org/10.2307/2333009]

저자소개

윤지현 : 고려대학교 산업경영공학부에서 2023년 학사 학위를 취득하고, 고려대학교 산업경영공학과에서 석사과정에 재학 중이다. 연구분야는 Tabular Data Synthesis, Generative Models이다.

추창욱 : 고려대학교 산업경영공학부에서 2023년 학사 학위를 취득하고, 고려대학교 산업경영공학과에서 석사과정에 재학 중이다. 연구분야는 Large Language Model, Time Series Forecasting이다.

허종국 : 고려대학교 산업경영공학부에서 2021년 학사 학위를 취득하고, 고려대학교 산업경영공학과에서 석박통합과정에 재학 중이다. 연구분야는 Self-Supervised Learning, Graph Neural Networks, Reinforcement Learning이다.

임새린 : 고려대학교 산업경영공학부에서 2021년 학사 학위를 취득하고, 고려대학교 산업경영공학과에서 석박통합과정에 재학 중이다. 연구분야는 Time-Series Deep Learning, Self-Supervised Learning이다.

정현빈 : 현대모비스 크리에이티브 UX 셀 책임연구원으로 재직 중이다.

김성범 : 고려대학교 산업경영공학부 교수로 2009년부터 재직하고 있으며, 인공지능공학연구소 소장, 기업산학연협력센터 센터장을 역임했다. 미국 University of Texas at Arlington 산업공학과에서 교수를 역임하였으며, 한양대학교 산업공학과에서 학사학위를 미국 Georgia Institute of Technology에서 산업시스템공학 석사 및 박사학위를 취득하였다. 인공지능, 머신러닝, 최적화 방법론을 개발하고 이를 다양한 공학, 자연과학, 사회과학 분야에 응용하는 연구를 수행하고 있다.

Hyperparameter	Value Search Space
Learning rate	[0.001, 0.0001, 0.00001]
Batch Size	[128, 256, 512]
Embedding Dimension	[64, 128, 256]
Hidden Dimension	[64, 128, 256]

System	Tire System			Braking System
Metric	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	0.784 ±0.026	0.200 ±0.006	0.047 ±0.008	0.515 ±0.048	0.014 ±0.003	0.048 ±0.003
CUSUM of Reconstruction Error	0.979 ±0.001	0.954 ±0.001	0.228 ±0.013	0.996 ±0.003	0.964 ±0.065	0.112 ±0.033
System	Steering System			Acceleration System
Metric	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	0.631 ±0.008	0.040 ±0.018	0.002 ±0.000	0.589 ±0.025	0.098 ±0.007	0.008 ±0.009
CUSUM of Reconstruction Error	0.997 ±0.004	0.991 ±0.009	0.070 ±0.020	0.999 ±0.000	0.990 ±0.000	0.153 ±0.002

	System	Tire System			Braking System
Metric	Backbone	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	LSTM	0.784 ±0.026	0.200 ±0.006	0.047 ±0.008	0.515 ±0.048	0.014 ±0.003	0.048 ±0.003
	1DCNN	0.787 ±0.001	0.188 ±0.001	0.014 ±0.006	0.702 ±0.008	0.028 ±0.005	0.014 ±0.005
	Transformer	0.642 ±0.024	0.194 ±0.022	0.027 ±0.007	0.554 ±0.010	0.029 ±0.003	0.009 ±0.004
CUSUM of Reconstruction Error	LSTM	0.979 ±0.001	0.954 ±0.001	0.228 ±0.013	0.996 ±0.003	0.964 ±0.065	0.112 ±0.033
	1DCNN	0.981 ±0.001	0.954 ±0.001	0.249 ±0.009	0.998 ±0.000	0.998 ±0.000	0.074 ±0.010
	Transformer	0.983 ±0.007	0.936 ±0.006	0.279 ±0.083	0.998 ±0.000	0.997 ±0.000	0.070 ±0.013
	System	Steering System			Acceleration System
Metric	Backbone	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	LSTM	0.631 ±0.008	0.040 ±0.018	0.002 ±0.000	0.589 ±0.025	0.098 ±0.007	0.008 ±0.009
	1DCNN	0.716 ±0.000	0.049 ±0.001	0.002 ±0.002	0.706 ±0.015	0.190 ±0.066	0.005 ±0.001
	Transformer	0.619 ±0.002	0.045 ±0.003	0.001 ±0.001	0.615 ±0.032	0.093 ±0.054	0.005 ±0.005
CUSUM of Reconstruction Error	LSTM	0.997 ±0.004	0.991 ±0.009	0.070 ±0.020	0.999 ±0.000	0.990 ±0.000	0.153 ±0.002
	1DCNN	0.999 ±0.003	0.995 ±0.000	0.057 ±0.001	0.999 ±0.000	0.967 ±0.015	0.166 ±0.040
	Transformer	0.999 ±0.000	0.998 ±0.000	0.063 ±0.001	0.998 ±0.001	0.980 ±0.011	0.116 ±0.056

	System	Tire System			Braking System
Metric	Model	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	LSTM-VAE	0.784 ±0.026	0.200 ±0.006	0.047 ±0.008	0.515 ±0.048	0.014 ±0.003	0.048 ±0.003
	USAD	0.914 ±0.000	0.197 ±0.000	0.027 ±0.001	0.884 ±0.000	0.115 ±0.001	0.049 ±0.001
	Anomaly Transformer	0.766 ±0.015	0.170 ±0.024	0.016 ±0.008	0.851 ±0.015	0.186 ±0.034	0.029 ±0.018
CUSUM of Reconstruction Error	LSTM-VAE	0.979 ±0.001	0.954 ±0.001	0.228 ±0.013	0.996 ±0.003	0.964 ±0.065	0.112 ±0.033
	USAD	0.979 ±0.000	0.939 ±0.000	0.311 ±0.000	0.962 ±0.000	0.820 ±0.001	0.010 ±0.000
	Anomaly Transformer	0.991 ±0.004	0.964 ±0.011	0.396 ±0.136	0.990 ±0.004	0.945 ±0.008	0.265 ±0.113
	System	Steering System			Acceleration System
Metric	Backbone	Robustness	Trendability	Monotonicity	Robustness	Trendability	Monotonicity
Reconstruction Error	LSTM-VAE	0.631 ±0.008	0.040 ±0.018	0.002 ±0.000	0.589 ±0.025	0.098 ±0.007	0.008 ±0.009
	USAD	0.922 ±0.000	0.144 ±0.001	0.036 ±0.003	0.890 ±0.000	0.006 ±0.000	0.033 ±0.000
	Anomaly Transformer	0.612 ±0.088	0.122 ±0.162	0.007 ±0.009	0.559 ±0.019	0.172 ±0.021	0.010 ±0.003
CUSUM of Reconstruction Error	LSTM-VAE	0.997 ±0.004	0.991 ±0.009	0.070 ±0.020	0.999 ±0.000	0.990 ±0.000	0.153 ±0.002
	USAD	0.987 ±0.000	0.093 ±0.008	0.077 ±0.001	0.997 ±0.000	0.990 ±0.014	0.157 ±0.000
	Anomaly Transformer	0.997 ±0.005	0.982 ±0.031	0.120 ±0.088	0.999 ±0.001	0.953 ±0.020	0.108 ±0.055