복수 포장대와 피킹-패킹 전환 정책을 운영하는 물류센터에서의 작업자 스케줄링

1. 서 론

오더 풀필먼트(order fulfillment)는 물류센터 운영의 주요 기능으로, 고객 주문 처리를 위해 물품 수령, 보관, 피킹(picking), 패킹(packing), 배송 단계를 포함한다(Croxton, 2003). 주문 피킹 및 패킹 단계는 노동집약적이고 고객 주문 처리의 속도와 정확성에 큰 영향을 미치므로 신중한 계획과 조직, 세부 사항에 대한 주의가 필요하다. 주문 피킹은 작업자가 보관 구역에서 필요한 모든 물품을 수집하여 특정 장소(depot)로 이동하는 단계로 물류센터 운영비의 55%를 차지한다(Bartholdi III and Hackman, 2019). 주문 패킹은 작업자가 수집한 물품을 검사하고, 주문 내용을 확인하거나 개수를 확인하며, 적합한 용기에 포장하는 단계이다.

이커머스(e-commerce) 업체를 포함한 물류센터의 관리자들은 실시간으로 도착하는 고객 주문을 처리하기보다는 고객의 기대와 행동에 대응하기 위한 웨이브(wave) 기반 주문 피킹 및 패킹 시스템을 활용한다. 해당 시스템은 특정 시간(즉, 웨이브) 내에 접수된 여러 고객의 주문을 공통된 배송 시간에 할당하고, 이를 동시에 처리한다(Rasmi et al., 2022). 각 웨이브는 일반적으로 1시간에서 4시간으로 계획된다(Piasecki, 2009). 본 시스템의 주요 목표는 총 작업완료시간(makespan)의 최소화이며, 작업자 간 작업완료시간의 균형화 및 작업자 가동률 개선에 도움을 준다(Ardjmand et al., 2018).

주문 피킹 및 패킹 단계는 다양한 작업자 운영 정책에 따라 수행된다. 대부분 물류센터는 피킹 및 패킹 단계를 독립적인 작업자 팀을 통해 수행하는 단일 작업 정책(monotasking policy - MT)을 활용한다. 해당 정책은 작업자의 전문화를 통해 안정적인 작업수행이 가능하다는 장점이 있지만, 피킹 및 패킹 단계 간의 인력 배치에 따라 효율성이 떨어질 수 있다(Zhong et al., 2022). 또 다른 작업 운영 정책인 피킹-패킹 전환 정책(pick-pack switching policy - SW)은 모든 작업자가 피킹 작업을 수행 후, 일부 작업자들은 복수의 포장대로 이동하여 패킹 작업을 순차적으로 수행한다. 해당 정책의 운영을 위해 작업자는 피킹 및 패킹 작업 모두에 능숙하여야 하지만, 패킹 작업자의 유휴 시간 최소화를 통해 총 작업완료시간을 단축시킬 수 있다는 장점이 있다.

본 연구는 웨이브 기반 주문 피킹 및 패킹 시스템에서 작업자 스케줄링을 위한 피킹-패킹 전환 정책을 다룬다. 본 연구의 목표는 각 웨이브의 총 작업완료시간을 최소화하기 위한 작업자 스케줄링 알고리즘을 개발하는 것이다. 본 연구의 주요 기여는 다음과 같다: (1) 복수 포장대 창고의 주문 피킹 및 패킹 과정에서 두 가지 작업자 운영 정책(MT 및 SW 정책)을 분석한다; (2) 두 가지 작업자 운영 정책을 운영하는 주문 피킹 및 패킹 시스템의 총 작업완료시간을 최소화하기 위한 작업자 스케줄링 수리모형을 제안한다; (3) SW 정책을 적용한 시스템의 작업자 스케줄링 문제 해결을 위해 Backward 스케줄링 결과를 초기해(initial solution)로 사용하는 시뮬레이티드 어닐링(Simulated Annealing, SA) 알고리즘을 제안한다.

본 논문의 구성은 다음과 같다. 제2장에서는 관련 문헌 연구를 제시하며, 제3장에서는 작업자 스케줄링의 문제 정의와 수리모형을 제안한다. 제4장에서는 SW 정책을 적용한 시스템의 작업자 스케줄링을 위한 휴리스틱 알고리즘을 제안한다. 제5장에서는 제안 알고리즘의 효과성 검증을 위한 실험 설계 및 결과를 제시한다. 마지막으로 제6장에서는 결론 및 향후 연구를 제시한다.

2. 문헌 연구

오더 풀필먼트는 물류센터 운영에서 핵심적인 역할을 수행하며 관련된 많은 연구가 수행되었다. 대부분의 선행 연구는 작업자와 관련된 문제를 오직 피킹 프로세스에 한정되어 수행되었다(Ardjmand et al., 2018; Kim and Hong, 2020; Scholz et al., 2017). 본 연구는 피킹 및 패킹 시스템에서 작업자 인력 배치 및 스케줄링에 중점을 두어 관련 문헌을 검토한다.

선행 연구는 작업자 운영 정책에 대해 단일 작업 정책(MT)과 피킹-패킹 전환 정책(SW)을 고려하였으며, 대부분의 연구는 작업자들이 피킹 또는 패킹 작업 중 하나에 할당되어 해당 작업만을 수행하는 MT 정책을 채택하였다. Badurdeen(2002)은 일정 시간 내에 주문 세트를 피킹 및 패킹하기 위한 최적 작업자 수를 결정하는 모델을 제안하였다. 해당 시스템 내 피킹된 물품은 컨베이어를 통해 패킹 구역으로 운송되어 작업이 수행된다. Gallien and Weber(2010)는 동적 피킹 및 웨이브 피킹 전략에서 주문 처리량을 극대화하고 정렬 및 패킹 작업자 가동률 예측을 위한 대기행렬 모형을 개발하였다. Zhong et al.(2022)은 물류센터에서 주문 피킹과 패킹이 독립된 작업자 팀에 의해 수행되는 시스템을 대상으로 통합 계획을 평가하였다. 해당 연구는 피킹 단계만의 개선은 전체 시스템 성능 향상을 할 수 없을뿐더러 이어지는 패킹 단계의 성능 저하로 이어질 수 있음을 보였다. 또한, 전체 시스템 성능은 각 단계의 인력 배치에 따라 상이할 수 있음을 제시하였다. Jiang et al.(2022)은 피킹 및 패킹 시스템에서 주문 배치 및 순서 결정을 통해 총 작업완료시간 단축을 위한 상황 기반 시드 알고리즘을 제안하였다. 해당 시스템에서 푸트 월(put wall)을 활용하여 패킹 작업자는 정렬 작업도 함께 수행하지만, 각 단계에 대해 단일 작업자를 고려하였다. Zhang et al.(2016)은 기존 연구와 달리 동일 작업자가 피킹 및 패킹을 함께 수행하는 정책을 고려하였으며, 패킹 시간은 피킹 시간에 포함된다고 가정하였다.

SW 정책과 관련하여, Kim(2009)만이 해당 정책을 고려하여 체류 시간 추정을 기반으로 한 동적 작업자 배정 정책을 제안하였다. 해당 문제는 고객 만족도를 극대화하기 위하여 작업자들이 피킹, 패킹, 배송 작업 간에 언제, 얼마나 전환할지를 결정하는 것을 목표로 한다. 문헌 연구를 통해 피킹 및 패킹 단계 간 작업자 운영 정책 중 SW 정책에 대한 연구는 부족한 실정임을 확인하였다. 따라서 본 연구는 복수 포장대를 활용하는 물류센터 내 SW 정책을 위한 작업자 스케줄링을 수행한다.

3. 문제 정의 및 수리모형

3.1 문제 정의

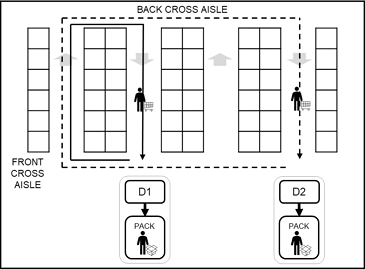
본 연구는 n_a개의 평행 통로와 앞뒤에 각각 하나씩 있는 교차 통로로 구성된 물류센터를 가정한다. 각 평행 통로는 양쪽에 n_h개의 제품 보관 선반이 있으며, 총 n_d개의 depot가 복수의 통로 앞에 배치된다. 각 depot는 피킹이 완료된 주문에 대한 패킹을 대기하며, 모든 depot는 사용 여부에 따라 활성화 depot와 비활성화 depot로 구분된다. 가용가능한 인력 n_w는 각 웨이브에서 작업가능한 총 작업자 수를 의미한다. <Figure 1>은 n_a = 4, n_h = 6, n_d = 2, 및 n_w = 4인 소규모 복수 포장대를 활용하는 물류센터 예시이다.

Figure 1.

An Example of the Target Warehouse

각 웨이브는 n_b개의 피킹 및 패킹 리스트로 구성되며, 각 리스트는 작업자가 수집해야 할 물품의 집합을 의미한다. 피킹 작업자는 활성화 depot에서 할당된 리스트 정보를 얻고, 통로를 따라 물품을 수집한 후 해당 depot로 돌아와 하역을 수행한다. 피킹 작업자는 S-shape routing 방법을 따른다고 가정하며, 모든 통로를 진입할 필요는 없지만 진입한 통로에 대해서는 단방향으로 통과하여야 한다(<Figure 1> 참조). 해당 방법은 사용이 간편하고 이해하기 쉬우며 별도의 계획 없이 적용된다는 점에서 널리 사용된다. 각 리스트에 대해 할당된 depot에서 가장 짧은 S-shape 경로가 선택된다. 작업자 이동속도는 일정하다고 가정하며 이동 시간은 오직 이동 거리에만 의존한다.

리스트의 피킹 시간은 정보 접수 시간, 이동 시간, 물품당 수집 시간, 그리고 하역 시간을 포함한다. 각 작업자에게 할당된 활성화 depot에 따라 이동 시간이 달라지므로, 적절한 depot의 선택은 각 리스트의 피킹 시간을 향상시킬 수 있다(Tran-Vo et al., 2022). 또한, 연속적으로 다른 depot에 할당된 리스트를 처리할 때, 웨이브의 작업완료시간에 영향을 미치는 작업자의 depot 간 이동 시간을 줄이는 것이 필요하다. 각 리스트의 패킹 시간은 고정되어 있으며, 검사 및 포장 시간을 합산하여 계산된다.

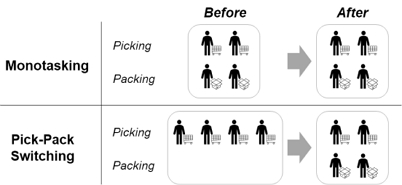
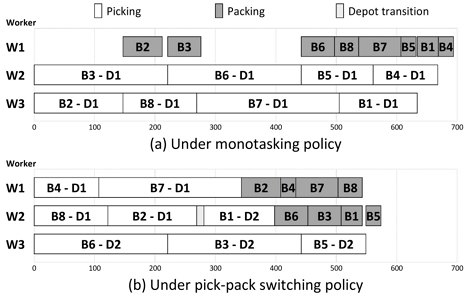
<Figure 2>는 두 가지 작업자 운영 정책인 MT과 SW의 작업자 배치를 나타낸다. MT 정책에서 작업자들은 사전에 피킹 또는 패킹 작업 중 하나의 작업에 배치되어 할당된 작업만을 수행한다. 이와 달리, SW 정책에서 모든 작업자는 피킹 작업을 시작하며 이후, 일부 작업자는 패킹 작업, 나머지 작업자는 계속 피킹 작업을 수행한다. 두 정책에서 패킹 작업에 배치될 수 있는 최대 작업자 수는 depot의 수에 의해 제한된다. 또한, 모든 작업자의 작업 효율은 동일하다고 가정한다.

Figure 2.

MT and SW Policies

각 작업자 운영 정책에 따른 작업자 스케줄링 문제(Worker scheduling problem in order picking and packing system-WPPS)는 피킹 및 패킹 단계의 총 작업완료시간 최소화를 위해 서로 다른 하위 문제로 구성된다. 이러한 하위 문제에 대한 수리모형을 다음과 같다.

3.2 수리모형

WPPS 문제에 대한 Mixed Integer Linear Programming(MILP) 수리모형을 위하여 Precedence-variable-based 방법(Demir and Isleyen, 2013)을 사용한다. 해당 방법은 각 작업자에 할당된 작업의 선후관계를 정의하기 위하여 이진변수를 사용한다. 하지만, 해당 변수는 반드시 즉각적인 순차적인 순서를 의미하지는 않는다. 다음으로, SW 정책에 대한 모형(WPPS-SW)을 제안한 후, MT 정책에 대한 모형(WPSS-MT)을 위한 추가 제약 조건을 제안한다. <Table 1>은 수리모형에서 사용된 모든 표기를 나타낸다.

Table 1.

Table of Notations

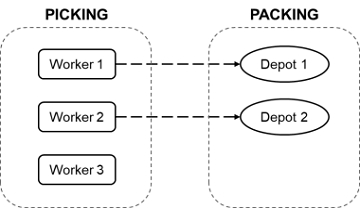
<Figure 3>은 변수, 제약 조건, 복수의 최적해 수를 줄이기 위한 Combined worker-depot 인덱싱 방법을 나타낸다. 인덱스가 depot와 일치하는 작업자만 해당 depot에서 패킹 작업을 수행할 수 있다. 따라서 특정 depot와 일치하는 작업자가 패킹을 수행하지 않으면, 해당 depot는 비활성 상태가 된다. 반면, 인덱스가 일치하는 depot가 존재하지 않는 작업자는 피킹 작업만 수행한다. 해당 인덱싱 방법을 적용하기 위해 작업자 수는 포장대 수를 초과해야 한다.

Figure 3.

Combined Worker-depot Indexing

해당 방법의 적용을 통해 WPPS는 피킹 및 패킹의 단계를 가진 2단계 Flexible Flowshop Scheduling(2단계 FFS) 문제로 변환된다. 각 단계에서 리스트는 해당 단계 작업을 수행할 수 있는 작업자 그룹에서 작업자에게 배정되어야 한다. 그러나 기존의 2단계 FFS와 달리, WPPS-SW와 WPPS-MT는 이러한 작업자 그룹이 사전에 고정되지 않으며 할당된 depot에 따른 피킹 시간의 차이가 발생한다. 특히, 2단계 FFS에서는 각 단계의 처리 시간이 해당 단계의 작업자 그룹에만 의존하지만, WPPS에서는 피킹 단계의 처리 시간이 패킹 단계에서 할당된 depot에 의존한다.

(1) WPPS-SW 모델

Combined worker-depot 인덱싱 방법을 통해 WPPS-SW 문제는 작업자에게 피킹 및 패킹 작업의 배정 이후, 순서를 지정하는 것으로 단순화한다. 해당 프레임워크에 따라, WPPS-SW 문제는 다음과 같이 공식화된다.

• Decision variables:
• X_bw = 리스트 b가 작업자 w에게 피킹이 할당되었는지 나타내는 이진 변수
• Y_bd = 리스트 b가 depot d에게 패킹이 할당되었는지 나타내는 이진 변수
• ZP_bb^′= 피킹 과정에서 리스트 b가 b^′를 선행하는지 나타내는 이진 변수
• ZD_bb^′= 패킹 과정에서 리스트 b가 b^′를 선행하는지 나타내는 이진 변수
• SP_b = 리스트 b의 피킹 시작 시간
• SD_b = 리스트 b의 패킹 시작 시간
• MT_bb^′= 리스트 b와 b^′이 할당된 depot 간의 이동 시간
• C_max= 총 작업완료시간
• 　
• Expressions:
• CP_b = 리스트 b의 피킹 완료 시간 = $$ S{P}_b+\sum _{d\in D}P{T}_{bd}{Y}_{bd}$$
• CD_b = 리스트 b의 패킹 완료 시간 = DT_b+CD_b
• 　
• Objective function:

$\[ \left(\mathrm{W}\mathrm{P}\mathrm{P}\mathrm{S}-\mathrm{S}\mathrm{W}\right)Min{ C}_{\text{max}} \]$

(1)

• Subject to:

$\[ \begin{array}{cc}\sum _{w\in W}{X}_{bw}=1\hfill & \forall b\in B,\hfill \end{array} \]$

(2)

$\[ \begin{array}{cc}\sum _{d\in D}{Y}_{bd}=1\hfill & \forall b\in B,\hfill \end{array} \]$

(3)

$\[ \begin{array}{cc}{SD}_b\ge {CP}_b\hfill & \forall b\in B,\hfill \end{array} \]$

(4)

$\[ S{P}_{b^{\prime }}\ge C{P}_b+M{T}_{b{b}^{\prime }}-\begin{array}{l}\left(3-X_{bw}-X_{b^{\prime }w}-Z{P}_{b{b}^{\prime }}\right)M\hfill \\ \mathrm{ }\mathrm{ }\mathrm{ }\forall w\in W,\forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(5)

$\[ \begin{array}{cc}Z{P}_{b{b}^{\prime }}+Z{P}_{b^{\prime }b}=1\hfill & \forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(6)

$\[ S{D}_{b^{\prime }}\ge C{D}_b-\begin{array}{c}\left(3-Y_{bd}-Y_{b^{\prime }d}-Z{D}_{b{b}^{\prime }}\right)M\hfill \\ \forall d\in D,\forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(7)

$\[ \begin{array}{cc}Z{D}_{b{b}^{\prime }}+Z{D}_{b^{\prime }b}=1\hfill & \forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(8)

$\[ S{D}_{b^{\prime }}\ge C{P}_b+M{T}_{b{b}^{\prime }}\begin{array}{l}-\left(2-X_{bw}-Y_{b^{\prime }d}\right)M\hfill \\ \left.\forall w\in W,\forall ,\forall \in D,\forall b,b^{\prime }\in B\right|\hfill \\ w=d,b\ne b^{\prime },\hfill \end{array} \]$

(9)

$\[ \begin{array}{cc}M{T}_{b{b}^{\prime }}\ge \sum _{d\in D}{L}_d{Y}_{bd}-\sum _{d\in D}{L}_d{Y}_{b^{\prime }d}\hfill & \forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(10)

$\[ \begin{array}{cc}M{T}_{b{b}^{\prime }}\ge \sum _{d\in D}{L}_d{Y}_{b^{\prime }d}-\sum _{d\in D}{L}_d{Y}_{bd}\hfill & \forall b,b^{\prime }\in B\left|b\ne b^{\prime },\right.\hfill \end{array} \]$

(11)

$\[ \begin{array}{cc}{C}_{\text{max}}\ge C{D}_b\hfill & \forall b\in B,\hfill \end{array} \]$

(12)

$\[ X_{bw},Y_{bd},Z{P}_{b{b}^{\prime }},Z{D}_{b{b}^{\prime }}\in \begin{array}{l}\left\{\mathrm{0,1}\right\}\hfill \\ \forall b,b^{\prime }\in B,\forall w\in W,\forall d\in D,\hfill \end{array} \]$

(13)

$\[ \begin{array}{cc}S{P}_b, S{D}_b, M{T}_{b{b}^{\prime }}, C_{\text{max}}\ge 0\hfill & \forall b,b^{\prime }\in B\left|b\ne b^{\prime }.\right.\hfill \end{array} \]$

(14)

목적함수 (1)은 총 작업완료시간을 최소화하는 것을 목표로 한다. 제약 조건 (2)와 (3)은 각 리스트를 피킹을 위한 작업자와 패킹을 위한 depot에 할당한다. 제약 조건 (4)는 리스트의 패킹이 피킹 완료 후에만 시작될 수 있도록 한다. 제약 조건 (5)와 (6)은 각 작업자의 피킹 작업 시작 시간을 순서에 따라 정의하고, depot 간 전환 시간을 고려한다. 제약 조건 (7)과 (8)은 depot의 순서에 따라 패킹 시작 시간을 정의한다. Combined worker-depot 인덱싱 방법에 따라 작업자 w(w ∊ D ⊂ W)는 모든 할당된 피킹 작업 완료 및 해당 depot d (d = w)로 이동한 후, 패킹 작업으로 전환하게 된다. 따라서 제약 조건 (9)는 첫 번째 패킹 시작 시간이 마지막 피킹 작업 완료 시간과 depot 간 작업자의 전환 시간을 더한 값보다 항상 크다는 것을 보장한다. 제약 조건 (10)과 (11)은 두 리스트 간의 창고 전환 시간을 첫 번째 depot에서 각 리스트에 할당된 depot까지의 이동 시간 간의 비음수 차이로 계산한다. 제약 조건 (12)는 웨이브 완성 시간을 모든 목록 중 가장 늦은 포장 완료 시간으로 정의한다. 제약 조건 (13)과 (14)는 각 결정 변수의 도메인을 정의한다.

(2) WPPS-MT 모델

WPPS-MT 문제는 WPPS-SW 모델에 depot의 활성 상태 여부를 나타내는 변수 U_d와 피킹 및 패킹 인력 배치를 다루는 제약 조건이 추가된다. 따라서, WPPS-MT 모델은 WPPS-SW 모델의 목적함수와 다음 제약 조건을 추가로 포함한다.

$\[ \begin{array}{cc}\sum _{b\in B}{X}_{bw}\le \left(1-U_d\right)M\hfill & \forall d\in D, \forall w\in W, w=d,\hfill \end{array} \]$

(15)

$\[ \begin{array}{cc}\sum _{b\in B}{Y}_{bd}\le U_{d}M\hfill & \forall d\in D,\hfill \end{array} \]$

(16)

$\[ \begin{array}{cc}{U}_d\in \left\{\mathrm{0,1}\right\}\hfill & \forall d\in D.\hfill \end{array} \]$

(17)

제약 조건 (15)는 패킹을 수행하는 작업자에게 피킹 작업에 할당되지 않도록 제한한다. 제약 조건 (16)은 패킹 작업이 오직 패킹 작업자에게만 할당될 수 있도록 한다. 제약 조건 (17)은 변수 U_d의 도메인을 정의한다.

4. 제안 알고리즘

4.1 Backward 스케줄링

Backward 스케줄링은 각 작업의 마감 시간이 존재할 때, 지연 또는 조기 완료를 최소화하기 위한 휴리스틱이다. 해당 스케줄링 방법은 첫 작업부터 순차적으로 하는 Forward 스케줄링 방법과 달리, 마지막 작업부터 시작하여 계획을 세운다.

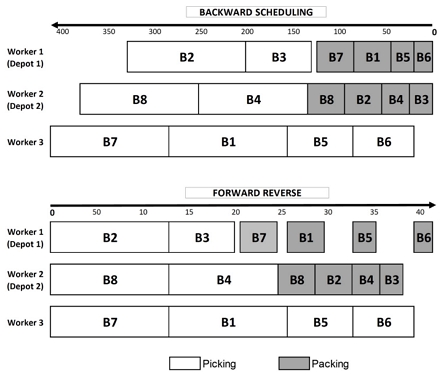
WPPS-SW 문제 해결에서 Backward 스케줄링은 두 가지 주요 이점을 제공한다. 첫째, 패킹을 위한 depot을 우선 선택함으로써 피킹 시간과 depot 간 전환 시간을 사전에 알 수 있다. 둘째, 패킹 작업의 우선 할당 및 현재 작업 부하를 고려한 피킹 작업 배정을 통해 총 작업완료시간을 단축할 수 있다. <Figure 4>는 제안하는 Backward 스케줄링 기반의 구성 휴리스틱(BW)이며 WPPS-SW 문제를 해결하기 위해 4단계로 구성된다.

Figure 4.

Backward Scheduling Method

BW에 따라, 먼저 패킹 작업을 할당하고 순서화한 후, 피킹 작업을 처리한다. 패킹 스케줄링에서는 패킹 시간이 적은 순서로 작업을 고려하고, 작업자는 작업자 배정(WA) 규칙에 따라 선택된다. 피킹 스케줄링에서는 작업 부하가 적은 작업자부터 고려하며, 작업 배정(BA) 규칙에 따라 피킹 작업을 할당한다. 모든 작업자의 작업 순서가 정해지면, 최종 해결책을 도출하기 위한 Forward 스케줄링을 진행한다(<Figure 5> 참조). Forward 스케줄링은 각 작업자에 대한 피킹과 패킹 작업의 선행 관계를 유지하면서 가능한 한 빨리 작업을 시작하도록 구현되며, 패킹 작업은 해당 피킹 작업이 완료 이후에만 시작된다. Forward 스케줄링 결과와 Backward 스케줄링 결과에서의 작업완료시간은 항상 일치한다.

Figure 5.

An Example of Solutions of Backward Scheduling and its Corresponding Forward Scheduling

4.2 SA 알고리즘

SA 알고리즘은 금속 열처리 과정에서 영감을 받은 최적화 기법이며 해 탐색 과정에서 지역 최적해에 빠지는 것을 방지하기 위해 확률적으로 임의의 해를 허용하며 탐색을 진행한다(Pinedo, 1995). 시간이 지나면서 온도(temperature)가 점차 감소하고 임의의 해를 받아들일 확률도 줄어들어, 최적 또는 근사 최적해로 수렴한다. SA 절차는 초기 온도, 냉각 계수, 반복 횟수 등 주요 매개변수를 포함하며, <Figure 6>에 요약되어 있다. 새로운 해를 정의하기 위해 세 가지 이웃 탐색 연산자를 사용한다. Pick_swap 연산자는 두 개의 무작위 리스트에서 피킹 작업의 위치를 교환하고, Pack_swap은 패킹 작업을 교환한다. 마지막으로 Reassignment 연산자는 무작위 리스트에 다른 작업자 또는 depot를 재할당한다.

Figure 6.

The Proposed SA Procedure

5. 실험 설계 및 결과

5.1 실험 설계

WPPS 문제에서 SW 정책 성능평가를 위해 여러 실험을 설계하였다. 물류센터의 통로 수에 따른 세 가지의 경우에 대한 실험을 수행하였다. 이때, 하나의 통로에 대하여 길이 15미터, 너비 3미터 공간 내, 양쪽에는 15개의 저장 위치로 구성되었다고 가정한다. 4개의 통로로 구성된 물류센터의 경우, 소규모 인스턴스(instance)를 분석하기 위해 고객 주문 수를 6, 7, 8개로 실험을 설계하였으며, 6개 및 8개의 통로로 구성된 물류센터의 경우에는 고객 주문 수를 25~200개로 다양한 규모로 실험을 설계하였다. 주문 당 물품 종류 수는 Uniform[1,3], 각 종류의 수량은 Uniform[1,5]을 가정하였으며, 이는 실제 데이터를 기반으로 한 Hong et al.(2012)의 연구를 참고하였다. Loading 시간, Unloading 시간, 물품당 수집 시간, 물품당 검사 시간, 포장 시간은 각 10초, 20초, 5초, 5초, 20초로 가정하였으며, 작업자의 이동속도는 0.5 m/s로 일정하다고 가정하였다. <Table 2>는 실험 설계에 대한 세부 정보이다. 각 실험마다 10개의 인스턴스를 생성하였다. IBM ILOG CPLEX Optimization Studio 20.0의 Python API를 사용하여 MILP 모델을 해결하며, 모든 실험은 Intel Core i5-10400 CPU와 16GB 메모리가 장착된 Windows 10 시스템에서 수행하였다.

Table 2.

Experimental Design

5.2 실험 결과

(1) MT 정책과 SW 정책 간의 성능 비교

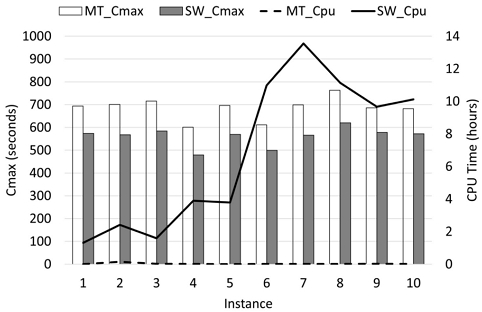
두 작업자 운영 정책의 성능을 분석하기 위해, 4개의 통로 내, 주문 8개를 처리하는 경우에 대해 MILP 모델을 실행하여 최적해를 계산하였다. <Figure 7>은 10개 인스턴스에 대해 각 정책별 최적해에 대한 성능 및 계산시간을 나타낸다. 전반적으로 SW 정책은 모든 인스턴스에 대해 총 작업완료시간을 MT 정책 대비 평균 18.12% 단축하였다. 그러나 MT 정책의 문제 해결을 위해 평균 89.8초가 소요되지만, WPPS-SW는 1.3~13.5시간의 상대적으로 더 많은 계산시간이 소요된다. <Figure 8>은 첫 번째 인스턴스에 대한 두 정책의 최적해를 제시한다. MT 정책의 결과에 따르면, 작업자 1은 패킹 작업을 수행하며 작업자 2와 3은 피킹 작업을 수행한다. 작업자 1은 작업자 2와 3이 피킹 작업의 완료까지 유휴시간으로 인한 낮은 가동률(53.31%)을 보이며, 해당 정책에서의 총 작업완료시간은 694초이다. 반면, SW 정책의 총 작업완료시간은 574초이며, MT 정책에 비해 17.29% 감소된 효과를 보인다. SW 정책의 최적해에서 모든 depot는 활성화되며 작업자 1과 2는 피킹 작업의 완료 이후, 패킹 작업을 수행한다. 이를 통해 SW 정책은 MT 정책 대비 각 작업자의 유휴시간 단축을 통해 작업자 가동률을 95.70%로 높일 수 있음과 동시에 작업량의 균등 분배에 기여할 수 있다.

Figure 7.

Performance Comparison between MT and SW Policies

Figure 8.

Optimal Solutions of Instance 1

(2) 제안 알고리즘 성능평가

제안 알고리즘의 성능을 여러 문제 규모에 대하여 평가하였다. BW와 SA의 경우, 각 인스턴스에 대한 20회 실행 후, 평균 결과를 산출한다. 또한, SA의 초기 온도는 50, 냉각 계수는 0.95, 반복 횟수(5000, 7500, 10000, 12500, 15000, 20000)는 주문량(25개 미만, 25, 50, 75, 100, 200)에 비례하게 설정하였다. 확장된 인스턴스의 최적해는 합리적인 계산시간 내 도출이 어려워 제안 알고리즘의 해 품질 평가를 위한 Lower Bound(LB)를 제안한다. LB는 항상 최적값보다 낮으며 알고리즘에서 도출된 목적값이 LB에 가까울수록 해당 목적값은 최적값에 더 근접함을 의미한다. 작업자 간의 최단 피킹 및 포장 시간 총합을 균등하게 분배하며 LB는 식 (18)을 통해 계산된다.

$\[ LB=\sum _{b\in B}\left({\text{min}}_{d\in D}P{T}_{bd}+D{T}_b\right)/n_w \]$

(18)

<Table 3>은 문제 규모에 따른 각 알고리즘의 성능평가 결과를 나타낸다.

• ∙ Cmax: 총 작업완료시간(초)
• ∙ Diff_LB: 알고리즘에서 도출된 Cmax와 LB 간의 차이 비율(%)
• ∙ Cpu: 알고리즘 통한 계산시간(초)

Table 3.

Algorithm Performance Evaluation

MILP의 경우, 합리적인 계산시간(2시간 이내라 가정) 내 4개 통로의 소규모 인스턴스에 대해서 해결이 가능하였다. 6개 및 8개 통로에 대하여 MILP의 계산시간을 3시간으로 제한하였을 때, 25~75개의 주문에 대하여 가능해(feasible solution)를 제공할 수 있었지만, 100개 이상의 주문에 대해서는 가능해를 제공하지 못하였다. LB는 소규모 인스턴스에서 최적해 대비 3.5~6.4%의 차이를 보였으며, 고객 주문 수가 증가할수록 MILP의 Diff_LB가 감소함을 통해 알고리즘 성능평가를 위해 수용할 수 있음을 확인하였다.

BW는 빠른 시간 내에 가능해를 제공할 수 있으며, 적은 주문량(25개 이하)에 대하여 MILP 대비 낮은 성능을 보였지만 많은 주문량(50개 이상)에 대해서는 더 높은 성능을 보였다. 또한, 6개 및 8개로 구성된 물류센터에서 적은 주문량을 처리할 경우, BW는 낮은 성능을 보였지만 많은 주문량을 처리할 경우, 우수한 성능을 보였다. BW의 결과를 초기해로 사용한 SA는 모든 인스턴스에 대하여 BW 대비 우수한 성능을 보였으며, 합리적인 시간 내에 가능해를 제공하였다. 또한, SA를 통한 해의 낮은 총 작업완료시간의 평균 및 표준 편차는 해당 알고리즘이 모든 문제 규모에 대하여 안정적인 해 도출이 가능함을 나타낸다.

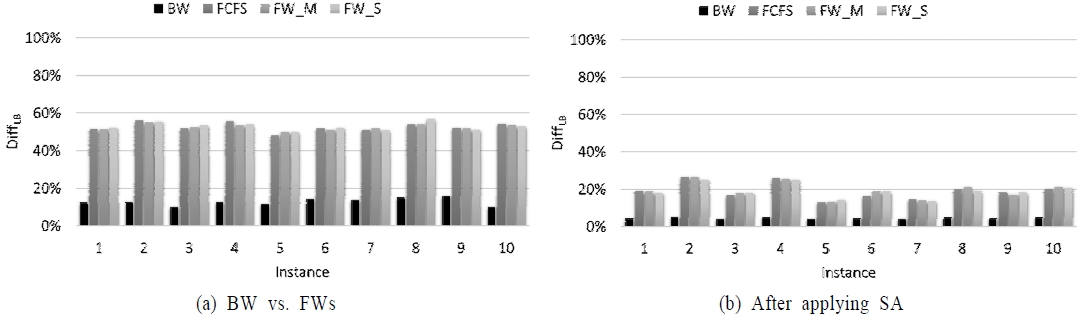
BW의 성능평가를 위하여 피킹 작업수행 이후 패킹 작업을 수행하는 3가지 Forward 휴리스틱(FW)을 고려하였다. 해당 휴리스틱들의 주요한 차이는 작업 선택 규칙에 있으며, 작업자/depot 배정 규칙은 가장 빠른 가용 시간 규칙에 따라 작업자 또는 depot를 선택한다. FCFS는 리스트를 선착순으로 고려한다. FW_M과 FW_S는 가장 짧은 처리 시간 규칙에 따라 리스트를 고려하지만, 피킹 과정에서 FW_M은 평균 처리 시간을 기준으로 하고, FW_S는 depot 간의 가장 짧은 시간을 기준으로 한다. <Figure 9>는 6개 통로로 구성된 물류센터에서 고객 주문 50개의 처리에 대하여 BW와 FW 간의 성능 결과 및 SA의 적용 이후의 성능 결과를 제시한다. BW는 WPPS-SW 문제 해결에서 FW들보다 우수한 해를 제공한다. SA 알고리즘 적용 이후, BW의 Diff_LB 값은 약 5%로, FW들의 15~25%에 비해 현저히 낮아진다. 해당 결과는 BW가 FW에 비해 작업자 유휴시간 대응에 유리하며, 작업자 간 균형적인 작업량 분배에 효과적임을 보여준다. 결과적으로 BW의 해는 SA 알고리즘의 효과적인 초기해로 활용가능하다.

Figure 9.

Performance Comparison between BW and FWs

6. 결 론

본 연구에서는 복수 포장대를 활용하는 물류센터 대상 주문 피킹 및 패킹 작업에서의 작업자 스케줄링 문제를 다룬다. 두 가지 작업자 운영 정책에 대하여 총 작업완료시간 최소화를 위한 MILP 모델을 제시하였다. 또한, 피킹-패킹 전환 정책 문제 해결을 위한 SA 알고리즘과 해당 알고리즘의 초기해를 위한 BW 휴리스틱을 제안하였다. 실험 결과는 MT 정책 대비 SW 정책이 효과적임을 보여주었으며, 해당 정책을 통하여 총 작업완료시간 단축 및 작업자 가동률을 향상시킬 수 있다. BW는 빠른 시간 내 문제 해결이 가능하며, Forward 스케줄링에 비해 우수한 해를 제공하였다. 추가로, BW의 해를 SA 알고리즘의 초기해로 사용하여 대규모 고객 주문에 대하여도 빠른 시간 내, 최적해와 근접한 해를 제공할 수 있었다.

향후 연구로 제안 알고리즘 성능개선과 해 도출을 위한 계산시간 단축이 있을 것이다. 본 연구에서 제안하는 Combined worker-depot 인덱싱 방법은 동일한 작업자를 가정하여 적용되었으나, 실사례에서는 작업자 간 숙련도는 상이할 수 있다. 따라서, 전체 작업시간을 개선하기 위하여 작업자의 숙련도를 고려한 작업 할당전략이 필요하다. 또한, 효과적인 주문 묶음은 이동 시간 및 포장 시간을 줄일 수 있어, 피킹 및 패킹 프로세스에서의 주문 묶음 문제를 통합적으로 해결하는 것이 중요하다. 마지막으로, 분류 및 배송과 같은 기타 창고 운영 프로세스를 통합하는 것도 다양한 운영 목표를 달성하기 위해 물류센터 전체 생산성을 향상시키는 유망한 연구 방향이다.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (the Ministry of Science and ICT) (No. NRF-2020R1A2C2004320).

References

• Ardjmand, E., Shakeri, H., Singh, M., and Bajgiran, O. S. (2018), Minimizing order picking makespan with multiple pickers in a wave picking warehouse, International Journal of Production Economics, 206, 169-183. [https://doi.org/10.1016/j.ijpe.2018.10.001]
• Badurdeen, F. F. (2002), Determining optimal staffing levels for the picking and packing operations in a distribution center, (Master Thesis), Ohio University.
• Bartholdi III, J. J. and Hackman, S. T. (2019), Warehouse & distribution science: Release 0.98.1 The Supply Chain and Logistics Institute, Georgia Institute of Technology, USA.
• Croxton, K. L. (2003), The order fulfillment process, The International Journal of Logistics Management, 14(1), 19-32. [https://doi.org/10.1108/09574090310806512]
• Demir, Y. and Isleyen, S. K. (2013), Evaluation of mathematical models for flexible job-shop scheduling problems, Applied Mathematical Modelling, 37(3), 977-988. [https://doi.org/10.1016/j.apm.2012.03.020]
• Gallien, J. and Weber, T. (2010), To wave or not to wave? Order release policies for warehouses with an automated sorter, Manufacturing & Service Operations Management, 12(4), 642-662. [https://doi.org/10.1287/msom.1100.0291]
• Hong, S., Johnson, A. L., and Peters, B. A. (2012), Batch picking in narrow-aisle order picking systems with consideration for picker blocking, European Journal of Operational Research, 221(3), 557-570. [https://doi.org/10.1016/j.ejor.2012.03.045]
• Jiang, X., Sun, L., Zhang, Y., and Hu, X. (2022), Order batching and sequencing for minimising the total order completion time in pick-and-sort warehouses, Expert Systems with Applications, 187, 115943. [https://doi.org/10.1016/j.eswa.2021.115943]
• Kim, H. H. (2009), Modeling service performance and dynamic worker allocation policies for order fulfillment Systems, (Ph.D Dissertation) Auburn University.
• Kim, Y. and Hong, S. (2020), Two picker cooperation strategies for zone picking systems with PTL technology, IEEE Access, 8(1), 106059-106070. [https://doi.org/10.1109/ACCESS.2020.2999342]
• Rasmi, S. A. B., Wang, Y., and Charkhgard, H. (2022), Wave order picking under the mixed-shelves storage strategy: A solution method and advantages, Computers & Operations Research, 137, 105556. [https://doi.org/10.1016/j.cor.2021.105556]
• Scholz, A., Schubert, D., and Wäscher, G. (2017), Order picking with multiple pickers and due dates–simultaneous solution of order batching, batch assignment and sequencing, and picker routing problems, European Journal of Operational Research, 263(2), 461-478. [https://doi.org/10.1016/j.ejor.2017.04.038]
• Tran-Vo, T. H., Nguyen, T. M., and Hong, S. (2022), Effects of Multiple Depots on Total Travel Distance in Parallel-Aisle Manual Order Picking Systems, IFIP International Conference on Advances in Production Management Systems. [https://doi.org/10.1007/978-3-031-16407-1_37]
• Zhang, J., Wang, X., and Huang, K. (2016), Integrated on-line scheduling of order batching and delivery under B2C e-commerce, Computers & Industrial Engineering, 94, 280-289. [https://doi.org/10.1016/j.cie.2016.02.001]
• Zhong, S., Giannikas, V., Merino, J., McFarlane, D., Cheng, J., and Shao, W. (2022), Evaluating the benefits of picking and packing planning integration in e-commerce warehouses, European Journal of Operational Research, 301(1), 67-81. [https://doi.org/10.1016/j.ejor.2021.09.031]