유전알고리즘을 활용한 중첩 대기시간 제약 플로우샵 스케줄링
© 2021 KIIE
Abstract
We examine a flow shop scheduling problem with overlapping waiting time constraints. The problem we consider is known to be NP-hard, and hence a mathematical optimization approach cannot solve large-sized instances within a reasonable computation time. Therefore, we propose a heuristic scheduling method using a genetic algorithm with local search. It is experimentally shown that the proposed algorithm is efficient and provides near-optimal solutions.
Keywords:
Scheduling, Genetic Algorithm, Flow Shop, Waiting Time Constraints1. 서 론
본 논문에서는 중첩 대기시간 제약(overlapping waiting time constraints)을 갖는 플로우샵(flow shop) 스케줄링 문제를 다루며, makespan 최소화를 목적으로 한다. 구체적으로 세 개의 공정설비를 갖는 3-설비 플로우샵을 대상으로 하며, 첫 번째 설비와 두 번째 설비 사이 그리고 첫 번째 설비와 세 번째 설비 사이에 각각 대기시간 제약이 존재한다. 두 시간 제약이 서로 중첩되므로 이러한 제약을 중첩 대기시간 제약이라고 부른다(Kim and Lee, 2019). 총 n개의 작업(job)이 있을 때 작업 i는, i = 1, ⋯, n, 첫 번째 설비에서 공정이 끝난 후 이내에 두 번째 설비에 투입되어 공정이 시작되어야 하며, 유사하게 첫 번째 설비에서 공정이 끝난 후 두 번째 설비에서의 공정시간을 제외하고 이내에 세 번째 설비에 투입되어 공정이 시작되어야 한다. 이러한 중첩 대기시간 제약은 반도체 제조에서 쉽게 관찰할 수 있다(Kim and Lee, 2019). 반도체 제조의 경우 총 공정의 약 20% 정도가 대기시간 제약을 통해 관리되며, 특히 확산(diffusion) 공정 후 세정(cleaning) 공정을 거쳐 다시 확산 공정으로 투입되는 작업의 경우 웨이퍼 품질 보장을 위해 본 논문에서 다루는 중첩 대기시간 제약에 의해 관리된다. 이 외에도 대기시간 제약은 배터리, 철강, 유제품 등의 생산에 있어 중요한 스케줄링 요구사항으로 다루어져왔다(Ju et al., 2017; Wang et al., 2010).
본 논문에서 다루고자 하는 문제는 NP-hard이므로, 문제의 크기가 커지면 혼합정수계획법(MILP) 또는 Branch and Bound(B&B) 알고리즘과 같은 최적화 방법을 사용하기에 한계가 있다(Kim and Lee, 2019). 따라서 본 논문에서는 중첩 대기시간 제약을 갖는 3-설비 플로우샵의 makespan 최소화를 목적으로 하는 스케줄링 문제를 해결하기 위해 유전알고리즘(genetic algorithm, GA) 및 지역탐색(local search) 기반 스케줄링 방법을 제안하며, 편의상 본 논문에서 제안되는 방법을 GALS(Genetic Algorithm with Local Search)라 한다. 참고로 GALS는 본 논문에서 처음 제안하는 방법론 또는 용어가 아니며 유전알고리즘과 지역탐색 기법을 활용한 최적화 혹은 스케줄링 방법을 통칭하는 용어임을 밝힌다(Tseng and Lin, 2009; Eroglu et al., 2014). 제안하는 스케줄링 방법은 초기모집단(initial population)의 우수성을 높이기 위한 휴리스틱 방법을 포함하며, 기존의 해를 바탕으로 더 좋은 해를 도출하기 위해 지역탐색 기반의 해 개선 방법 또한 포함한다.
본 논문의 구성은 다음과 같다. 우선 제 2장에서 본 연구와 관련된 문헌을 소개하고, 제 3장에서 본 연구에서 다루고자 하는 문제에 대한 구체적인 설명을 제시한다. 제 4장에서는 GALS를 제안하며, 제 5장에서는 실험을 통해 제안된 방법의 성능을 검증한다. 마지막으로 제 6장에서는 본 연구의 결론을 제시하고, 향후 연구에 관해 논의한다.
2. 관련문헌
플로우샵 스케줄링에 관한 연구는 지금까지 많은 연구자들에 의해 수행되어져 왔다. 일례로, Blazewics et al.(2001)은 두개의 설비를 갖는 플로우샵 스케줄링을 위해 지역탐색 기반의 휴리스틱 알고리즘을 제안하였다. Cheng et al.(2014)은 작업 종료시간의 합을 최소화하기 위하여 B&B 알고리즘을 제안하였다. 이외에도 플로우샵 스케줄링에 관한 연구로는 다음과 같은 논문들을 참고할 수 있다(Croce et al., 2014; Wu et al., 2013; Woo et al., 1996; Lee, 2006).
전술한 바와 같이 플로우샵 스케줄링에 관한 연구는 많이 이루어졌지만, 본 연구에서 다루고자 하는 핵심 스케줄링 요구사항인 대기시간제약을 고려한 연구는 비교적 많이 이루어지지 않았다. Yang and Chern(1995)은 대기시간제약이 있는 2-설비 플로우샵 스케줄링 문제가 NP-hard임을 보였고, makespan 최소화를 위해 B&B 알고리즘을 제안하였다. 또한 Joo and Kim(2009)은 대기시간제약이 있는 2-설비 플로우샵의 스케줄링을 위해 다양한 속성들을 분석하고 분석된 속성들을 바탕으로 효율적인 B&B 알고리즘을 개발하였다. An et al.(2016)은 앞서 다루어진 문제들을 sequence-dependent 셋업 시간으로 확장한 연구를 수행하였다. 이 외에도 Bouquard and Lente(2006)는 연속된 공정 사이에 최소 및 최대 지연이 있는 2-설비 플로우샵의 스케줄링을 위해 B&B 알고리즘을 제안하였다. 전술한 연구들 이외에도 대시시간 제약을 다룬 플로우샵 스케줄링 연구로는 다음의 연구들을 참고할 수 있다(Yu et al., 2017; Fondrevelle et al., 2006; Hamdi and Loukil, 2015; Attar et al., 2014).
기존 연구들 중 본 논문에서 다루고자 하는 연구와 가장 유사한 연구는 Kim and Lee(2019)이다. 구체적으로 Kim and Lee (2019)은 중첩 대기시간 제약이 있는 3-설비 플로우샵의 makespan 최소화를 위해 B&B 알고리즘을 제안하였다. 제안된 B&B 알고리즘은 최적해(optimal solution)를 제공한다는 장점이 있지만, 연구에서 다루어지는 문제가 NP-hard이므로 문제 크기가 커지면 일정 시간 내에 해를 도출하기가 어렵다. 구체적으로 작업물의 수가 50개인 경우 최적해를 얻을 때까지 평균 1시간 이상 소요되며 경우에 따라서는 해를 도출하지 못하는 경우도 있다 (Kim and Lee, 2019). 본 연구에서는 문제 크기가 큰 경우에도 빠른 시간 내에 최적해에 근사한 우수한 해를 도출하는 것을 목표로 한다.
이러한 목표를 달성하기 위해 적용할 수 있는 대표적인 방법 중 하나는 메타휴리스틱이다. 지금까지 스케줄링 문제에 적용 가능한 다양한 메타휴리스틱이 개발되었으며, 각각의 방법들은 장단점이 있으며 어느 한 방법론이 다른 방법론보다 절대적으로 우수하다고 판단하기는 어렵다. 플로우샵 스케줄링 문제에 메타휴리스틱이 적용된 예를 살펴보면, Rajendran and Ziegler(2004)는 순열 플로우샵의 makespan 및 총 flowtime의 최소화를 위해 ant-colony 최적화 알고리즘을 활용하였다. 동일한 문제에 대하여 Tasgetiren et al.(2007)은 particle swarm 알고리즘 기반 스케줄링 방법을 제안하였다. 전술한 연구들에 이어 Tseng and Lin(2009)은 순열 플로우샵 스케줄링 문제에 유전알고리즘을 적용하였다. 이외에도 Eroglu et al.(2014), Vallada and Ruiz(2011) 등이 생산 스케줄링 문제에 유전알고리즘을 적용하여 빠른 시간 내에 우수한 해를 얻을 수 있음을 보였다. 이러한 결과들을 토대로 본 논문에서는 빠른 시간 내에 최적해에 근사한 우수한 해를 도출하기 위해 유전알고리즘의 사용을 제안한다.
3. 문제정의
본 연구에서는 3개의 설비(M1, M2, M3)와 n개의 작업(1, 2, ⋯, n)이 있는 순열(permutation) 플로우샵 문제를 다룬다. 순열 플로우샵에서는 모든 설비에서의 작업 순서가 동일하다. 즉, M1에서 1, 2, ⋯, n의 순서로 공정이 이루어졌다면, M2와 M3에서도 동일한 순서로 공정이 진행된다. 순열 스케줄이 본 연구에서 다루는 문제에서 최적해를 항상 보장하지는 않지만, 순열 스케줄의 단순성, 운영용이성 등으로 인해 실제 생산현장에서 널리 사용되며 다수의 기존 연구에서도 순열 스케줄을 가정하였다(Kim and Lee, 2019; Joo and Kim, 2009; An et al., 2016).
작업 i, i = 1, 2, ⋯, n는 M1, M2, M3에서 각각 pi1, pi2, pi3의 공정시간을 가진다. 작업 i의 M1, M2, M3에서의 공정 종료시각을 각각 ci1, ci2, ci3이라 하면, 앞서 1장에서 소개한 대기시간 제약에 따라 아래의 두 가지 제약을 만족해야 한다.
| (1) |
| (2) |
식 (1)에서 ci2 - pi2는 M2에서 i의 공정 시작시각이므로 i가 M1에서 공정이 종료된 후 M2에서의 공정 시작이 이내에 이루어져야 함을 의미한다. 유사하게 식 (2)는 i가 M1에서 공정이 종료된 후 M3에서의 공정 시작이 이내에 이루어져야 함을 의미한다. 이때, M2에서의 공정시간(pi2)은 포함하지 않는다.
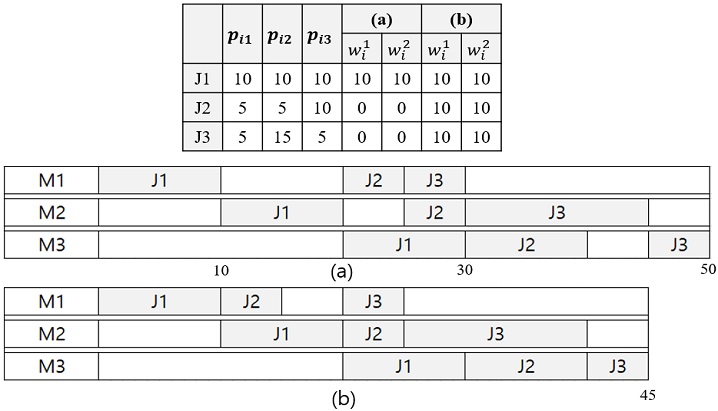
<Figure 1>을 통하여 대기시간 제약이 전체 스케줄에 어떤 영향을 미치는지 살펴볼 수 있다. <Figure 1>은 작업이 3개(J1, J2, J3)인 간단한 예제를 보여주며, 주어진 공정시간에 대해 두 종류의 서로 다른 대기시간 제약 (a)와 (b)를 가정한다. 그림의 위쪽 표는 공정시간 및 대기시간 제약에 대한 정보를 나타내며, 아래의 Gantt 차트 (a)와 (b)는 각각 대기시간 제약이 (a)와 (b)일 때의 생산 스케줄을 보여준다. 단, 작업순서는 J1, J2, J3으로 가정한다. 그림에서 살펴볼 수 있듯이 동일한 작업순서와 공정시간을 갖더라도 대기시간 제약이 달라짐에 따라 전체 생산 스케줄 및 makespan이 달라짐을 알 수 있다. 이러한 특성은 다음과 같이 수학적으로 일반화하여 표현 가능하다. 작업들의 순서를 나타내는 특정 작업 스케줄(또는 작업순서)에서 i번째에 위치한 작업을 [i]로 표현하며, 해당 작업의 공정시간 및 공정 종료시각 또한 각각 p[i]m과 c[i]m, m = 1, 2, 3으로 표현한다. 식 (1)과 식 (2)의 중첩 대기시간 제약으로 특정 스케줄 σ가 주어졌을 때 M1, M2, M3에서 σ의 i번째 작업 종료시각(c[i]1, c[i]2, c[i]3)은 다음과 같이 표현된다 (Kim and Lee, 2019).
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
위에 제시된 수식들을 통하여 임의의 스케줄이 주어졌을 때, 각 작업의 종료시각 및 전체 makespan을 쉽게 도출할 수 있다. 도출된 makespan은 향후 제안될 GALS에서 유전자의 우수성을 나타내는 적합도(fitness)로 사용된다.
4. Genetic Algorithm with Local Search
본 장에서는 유전알고리즘과 지역탐색 기법을 활용한 스케줄링 방법을 제안한다. 유전알고리즘은 자연세계의 진화과정에서 영감을 받아 개발된 여러 메타휴리스틱 중의 하나로, 스케줄링 문제에 널리 사용되고 있다. 유전알고리즘의 세부 부분은 실제 진화 과정에서 많은 부분을 차용하였으며, 구체적으로 선택, 교차, 변이 등의 과정을 포함한다. 본 논문에서 제안하는 스케줄링 방법을 아래 각 세부 절을 통해 설명한다.
4.1 유전자 표현방법 및 적합도
본 논문에서는 makespan 최소화를 목적으로 순열 플로우샵 스케줄링 문제를 다루므로 결정되어야 하는 사항은 각 작업의 순서이다. 각 작업의 순서가 결정되고 나면, 3장에서 제시된 수식들을 통해 각 설비에서의 작업 종료시각 및 전체 makespan을 도출할 수 있다. 따라서 본 연구에서는 유전자를 아래 <Figure 2>와 같이 표현한다(n = 5 즉, 1부터 5까지 총 5개의 작업이 있는 예). <Figure 2>의 유전자는 각 설비에서 1, 5, 3, 2, 4의 순서로 공정이 이루어져야 함을 나타낸다.
<Figure 2>의 예와 같이 유전자가 표현되면, makespan을 쉽게 도출할 수 있으며 해당 makespan은 유전자의 적합도로 사용된다.
4.2 초기모집단(initial population)
초기모집단을 구성하는 방법은 매우 다양하며, 가장 간단한 방법으로는 무작위(random) 방법이 있다. 구체적으로 각 작업별로 난수를 할당하고 할당된 난수들을 바탕으로 오름차순(또는 내림차순) 정렬을 함으로써 무작위 작업순서를 갖는 유전자를 얻을 수 있다. 하지만 초기모집단에 우수한 유전자가 많이 존재해야 향후 교차, 변이 등을 통해 더욱 우수한 유전자를 얻을 수 있고 최적해에 더 빨리 도달할 수 있으므로 잘 알려진 휴리스틱을 통해 초기 유전자를 생성하는 방법이 널리 사용된다(An et al., 2016; Kim and Lee, 2019). 따라서 본 연구에서는 다음과 같은 세 가지 휴리스틱을 이용하여 초기모집단을 구성하고 부족한 유전자는 무작위 방법으로 생성하여 초기모집단을 구성한다.
Johnson’s 알고리즘은 makespan 최소화를 목적으로 하는 2-설비 플로우샵 스케줄링 문제의 최적해를 제공함이 알려져 있다. 또한 3-설비 플로우샵 스케줄링에서도 특정 조건들이 만족될 경우 Johnson’s 알고리즘을 통해 최적해를 얻을 수 있다. 스케줄링 문제의 목적과 제약에 따라 Johnson’s 알고리즘을 경미하게 변형하여 적용한 예가 많이 있으며 기본적인 형태는 Johnson’s 알고리즘을 따르므로 유사함을 밝힌다(Joo and Kim, 2009; An et al., 2016; Kim and Lee, 2019). 본 논문에서 다루고자 하는 문제의 경우 중첩 대기시간 제약이 있으므로 Johnson’s 알고리즘을 통해 최적해를 도출할 수 있다는 보장은 없지만, 비교적 우수한 작업순서를 도출하기 위해 Johson’s 알고리즘을 변형한 Modified Johson’s 알고리즘을 사용한다. 이러한 접근은 본 연구에서 다루는 문제의 B&B 알고리즘 개발 시에도 사용되었다(Kim and Lee, 2019). 구체적인 알고리즘은 다음과 같다.
- Step 1 : 가상의 2-설비 플로우샵을 가정하고 각 작업은 첫 번째 설비에서 , 두 번째 설비에서 의 공정시간을 갖는다고 가정한다. 단, , ,
- Step 2 : 이전 단계에서 가정한 가상의 2-설비와 작업들에 대하여 Johnson’s 알고리즘을 적용하여 작업 순서를 도출한다.
Nawaz et al.(1983)에 의해 제안되고 저자들 이름의 첫 글자 조합으로 명명된 NEH 알고리즘은 복잡도가 낮고 우수한 해를 제공한다는 장점 때문에 일반적인 n개의 작업, m개의 설비를 갖는 플로우샵의 makespan 최소화 문제에 널리 사용된다. 해당 알고리즘에서는 우선 작업들을 작업시간의 총합에 따라 내림차순으로 정렬하고, 정렬된 순서에 따라 순차적으로 각 작업들을 최적의 위치에 배치시킨다. 본 연구에서는 중첩 대기시간 제약을 고려하므로, NEH 알고리즘을 그대로 적용하기는 불가능하며 따라서 아래와 같은 Modified NEH 알고리즘을 통하여 초기 유전자를 위한 작업순서를 결정한다(Kim and Lee, 2019).
- Step 1 : 설비 1, 2, 3에서의 공정시간 총합(pi1 + pi2 + pi3)을 기준으로 작업물들을 내림차순으로 정렬하고, 해당 순서를π 라고 하자. σ는 부분 작업순서를 나타내며, 초기에는 할당된 작업이 없다.
- Step 2 : π 에 작업물이 없을 경우, 종료한다. 그렇지 않으면, π 의 첫 번째 작업을 선택하고 π 에서 해당 작업을 삭제한다. 선택된 작업을 현재까지 결정된 부분 순서인 σ의 모든 가능한 위치에 넣어보고 makespan이 최소가 되는 곳에 최종적으로 위치시킨다. Step 2를 반복한다(단, 모든 후보 위치에 할당 시 makespan을 도출하기 위해 3장에 제시된 작업종료시간에 관한 수식을 활용한다).
Greedy 알고리즘의 기본적인 개념은 현재 상태에서 가능한 대안들 중 가장 좋은 대안을 선택해 나가는 방식이다. 따라서 본 연구에서 다루는 문제에서는 일부 작업의 순서가 이미 결정된 상태에서 다음 순서의 작업을 결정할 때 모든 가능한 즉, 아직 순서가 결정되지 않은 모든 작업을 대상으로 각 작업이 마지막 위치에 할당되었을 때 makespan의 증가가 최소가 되는 작업을 선택하게 된다. 구체적인 알고리즘은 다음과 같다.
- Step 1 : 설비 1, 2, 3에서의 공정시간 총합(pi1 + pi2 + pi3)이 최소인 작업을 첫 번째 순서로 결정한다. 순서가 결정된 작업의 수를 나타내는 인덱스 k를 정의하고 k = 1로 설정한다.
- Step 2 : k = n인 경우 종료한다. 그렇지 않은 경우, 아직 순서가 결정되지 않은 모든 작업을 각각 k + 1번째 위치에 할당해보고 makespan 증가량이 가장 작은 작업을 k + 1번째 순서에 최종 할당한다. k를 k + 1로 업데이트한다. Step 2를 반복한다.
향후 5장에서 실험을 통해 초기모집단 구성을 위한 휴리스틱 방법의 효과성을 검증한다.
4.3 선택(Selection)
유전알고리즘에서는 이전 세대의 유전자들을 바탕으로 교차, 변이 등을 통해 새로운 유전자들이 추가되고, 이 중 일부 유전자들이 ‘선택’ 과정을 통해 다음 세대로 전달되게 된다. 선택을 위해 활용할 수 있는 방법으로는 룰렛 휠, 토너먼트 선택, 순위 기반 선택 등이 있으며, 본 논문에서는 대표적인 선택 방법 중 하나인 룰렛 휠 방식의 사용을 제안한다(Moon, 2003). 룰렛 휠 방식의 기본 개념은 우수한 유전자일수록 다음 세대로 전달될 확률을 높여주는 것이다. 뿐만 아니라 비교적 덜 우수한 유전자에게도 다음 세대로 전달될 수 있는 일정 확률을 부여함으로써 다양성을 담보한다. 앞서 소개한 바와 같이, 본 연구에서는 유전자가 가지고 있는 작업 순서를 바탕으로 makespan을 계산하고 해당 makespan을 적합도로 사용한다. 따라서 본 연구에서는 적합도(makespan)가 낮을수록 좋은 유전자임을 나타내고 따라서 다음 세대로 전달될 확률을 높여주어야 한다. 이를 위해 아래와 같은 수식을 통해 각 유전자의 다음 세대 전달 확률을 정의한다.
| (9) |
위의 수식에서 Pi는 유전자 i가 다음 세대로 전달될 확률이며, 는 유전자 i의 적합도(makespan)인 fi 를 변형한 값이다. 적합도가 낮을수록 높은 확률을 부여하기 위해 가 사용되며, 다음의 수식과 같이 정의된다. . 즉, 현재 세대의 모든 유전자들의 적합도 중 가장 큰 값()과 특정 유전자의 적합도 차이를 활용하며, 그 값이 클수록 높은 확률을 부여 받는다.
앞서 정의된 대로 각 유전자에 대한 다음 세대 전달 확률 Pi가 계산되면 각 확률에 따라 미리 정의된 모집단 수만큼의 유전자가 선택되어 다음 세대로 전달되게 된다.
4.4 교차(Crossover)
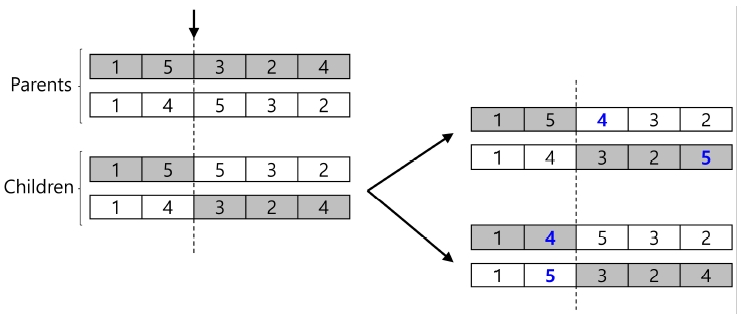
‘교차’는 두 부모 유전자의 조합을 통해 새로운 자식 유전자를 만들어 내는 과정을 의미한다. 교차를 위해 일반적으로 사용되는 방법 중 하나는 일점(one-point) 교차이며 이는 <Figure 3>과 같이 표현 가능하다(Moon, 2003). <Figure 3>의 왼쪽에 표현된 바와 같이 교차가 일어날 한 점을 무작위로 선정하게 되며, 해당 점을 기준으로 부모 유전자들의 교차가 일어나 자식 유전자가 생성된다. 본 연구에서 제안하는 유전자 표현방식에 일점 교차를 적용할 경우, 자식 유전자가 특정 작업을 2번 가지는 (또는 특정 작업을 가지고 있지 않은) 경우가 발생한다. 예를 들어 <Figure 3>의 첫 번째 자식 유전자의 경우 작업 5를 두 번 포함하며, 작업 4는 가지고 있지 않다. 간단한 처리를 통해 이러한 문제를 해결가능하다. <Figure 3>의 오른편에 제시된 것과 같이 선택된 점의 왼쪽 작업들을 기준으로 오른쪽 작업을 보정해주거나 반대로 오른쪽 작업들을 기준으로 왼쪽 작업들을 보정해줄 수 있다. <Figure 3>의 굵은 파란색으로 표현된 작업들이 보정된 작업들을 의미한다.
본 논문에서는 앞서 언급한 보정 방식을 모두 사용하며, <Figure 3>과 같이 2개의 부모 유전자를 교차할 경우 최종적으로 4개의 자식 유전자가 생성되며 해당 유전자들을 모집단에 포함시킨다. 교차에서 사용되는 파라미터로는 교차 비율이 있다. 교차 비율은 일반적으로 0에서 1 사이의 값으로 정의하며, (모집단의 유전자 수×교차 비율) 만큼의 교차가 일어난다. 본 연구에서는 각 교차에 필요한 부모 유전자를 무작위로 선정하는 방식을 사용한다.
4.5 변이(Mutation)
모든 유전자를 대상으로 0에서 1사이의 난수를 생성하고 해당 난수가 미리 정해진 변이 확률보다 작을 경우, 해당 유전자를 바탕으로 변이 유전자를 추가로 생성하여 모집단에 포함시킨다. 본 연구에서는 유전자가 가지는 작업 순서에서 두 작업을 무작위로 선정하여 해당 작업들의 위치를 교환하는 방식을 사용한다.
4.6 지역탐색(Local Search)
유전알고리즘의 성능을 높이기 위하여 추가적으로 지역탐색 기법을 활용한다. 지역탐색 기법은 비교적 계산 복잡도가 높기 때문에 모든 유전자에 대하여 수행하지는 않으며, 매 세대별 모집단에서 적합도를 기준으로 가장 좋은 5%의 유전자에 대해서만 지역탐색 기법이 적용되도록 디자인하였다. 구체적으로는 아래의 두 가지 방법을 활용한다.
가장 기본적인 지역탐색 기법으로는 특정 위치의 작업을 다른 위치로 옮기는 삽입(insertion) 방법과 특정 두 작업의 위치를 맞바꾸는 교환(exchange) 방법이 있다. 일반적으로 순열 플로우샵 스케줄링에서는 삽입 방법이 교환 방법에 비해 더 좋은 결과를 도출한다는 것이 알려져 있다(Tseng and Lin, 2009). 또한 교환 방법은 본 논문에서 제안하는 변이 과정에서 사용되므로 삽입 방법을 지역탐색 기법으로 활용한다. 구체적으로 유전자가 가지고 있는 모든 작업들에 대해 모든 가능한 위치에 삽입해 보고 가장 작은 makespan을 주는 경우를 선택하여 작업순서를 변경함으로써 유전자를 개선한다. 구체적인 알고리즘은 아래와 같다.
- Step 1 : BestMakesapn = ∞. π*는 삽입 방법으로 도출하게 될 최적 작업순서를 의미한다. 현재 유전자가 보유하고 있는 작업순서를 π라 하자. π상의 특정 작업의 위치를 나타내는 인덱스 i를 정의하고 초기값으로 1을 할당한다.
- Step 2 : π의 i번째 작업을 j, 번째 위치로 옮겨 삽입하여 새로운 작업순서 πʹ를 얻는다. πʹ의 makespan을 계산하고 TempMakespan에 저장한다. TempMakespan이 BestMakesapn보다 작으면 BestMake span을 TempMakespan으로 업데이트하고 π*를 πʹ로 업데이트 한다. i를 1 증가시킨다.
- Step 3 : 만약 i가 주어진 총 작업의 수 n보다 크면 알고리즘을 종료하고 해당 유전자의 작업순서를 π*로 변경한다. 그렇지 않으면, Step 2로 이동한다.
분리의 개념은 Tseng and Lin(2009)에서 제안되었다. 특정 작업 순서가 주어졌을 때 연속된 두 작업 쌍(pair)을 모두 조사하여 두 작업들 사이의 유휴시간(idle time)이 가장 큰 쌍을 makespan을 증가시키는 좋지 않은 작업 쌍으로 판단하며 두 작업을 분리하여 새로운 작업 순서를 도출하는 개념이다. 구체적으로 Tseng and Lin(2009)에서 제안된 방법은 큰 유휴시간을 갖는 작업 쌍 사이에 다른 하나의 작업을 삽입하여 쌍을 이루는 두 작업을 분리하고 새로운 작업순서를 얻는 방법을 제안하였다.
본 연구에서 제안하는 분리 및 재배치 방법은 유휴시간이 큰 작업 쌍을 분리한다는 개념에서는 Tseng and Lin(2009)에서 제안된 방법과 동일하지만, 새로운 작업 순서를 생성 시 기존에 쌍을 이루고 있던 연속된 두 작업을 서로 연속하지 않으면서 위치할 수 있는 모든 가능한 위치에 삽입해 본다는 점에서 차이가 있다. 이러한 분리 및 재배치의 경우 Tseng and Lin(2009)에서 제안된 방법보다 더 많은 작업 순서 대안들을 탐색하게 된다는 점에서 더 좋은 해를 얻을 수 있는 가능성이 있다. 다만, Tseng and Lin(2009)에서 제안된 방법에 비해 계산시간이 더 오래 걸린다는 단점이 있다.
구체적인 알고리즘은 아래와 같이 기술 가능하다.
- Step 1 : BestMakesapn = ∞. π*는 분리 및 재배치 방법으로 도출하게 될 최적 작업순서를 의미한다. 현재 유전자가 보유하고 있는 작업순서를 π라 하자. π에서 분리가 이루어져야 할 작업들의 위치인 i와 i + 1을 아래와 같이 결정한다.
.
- Step 2 : π의 i번째 작업을 j, 번째 위치로, i + 1번째 작업을 k, 번째 위치로 각각 옮겨 삽입하여 새로운 작업순서 πʹ를 얻는다 (단, ). πʹ의 makespan을 계산하고 TempMakespan에 저장한다. TempMakespan이 BestMakesapn보다 작으면 BestMakespan을 TempMakespan으로 업데이트하고 π*를 πʹ로 업데이트 한다.
- Step 3 : 유전자의 작업순서를 π*로 변경하고 알고리즘을 종료한다.
위 알고리즘에서 는 주어진 임의의 작업 순서에서 j번째 작업과 j + 1번째 작업 사이의 유휴시간을 의미하며 c[j]k는 앞서 3장에서 제시된 수식으로 계산한다.
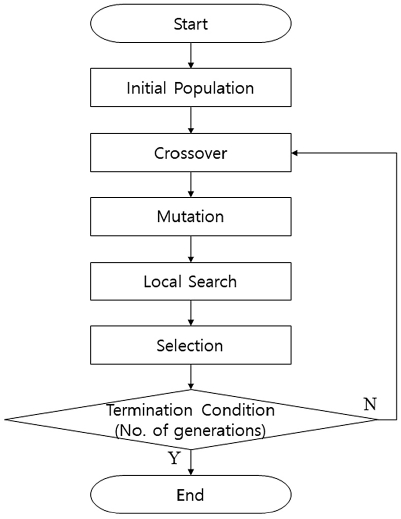
본 논문에서 제안하는 스케줄링 방법은 미리 지정된 최대 세대수에 도달하면 종료되며, 전체 흐름은 아래 <Figure 4>와 같이 표현가능하다.
앞서 본장 2절에서 소개된 알고리즘들을 활용하여 초기모집단을 구성하고, 초기모집단에 대해 각각 본장의 4절, 5절, 6절에서 소개된 교차, 변이, 지역탐색을 통해 유전자의 다양성을 높이고 해의 개선을 추구한다. 이후 현재 모집단에서 다음세대로 전달될 유전자들을 선택과정을 통해 선별하게 되며 이러한 과정이 최대 세대수에 도달할 때가지 반복된다.
5. 실험결과
제안된 GALS의 구현을 위해 Java 프로그래밍 언어를 사용하였고, 모든 실험은 PC(Intel Core i7-9700, 32GB RAM)에서 진행되었다.
5.1 파라미터 설정
본 연구를 통해 제안하는 GALS에 사용되는 파라미터를 설정하기 위한 예비실험을 진행하였다. 예비실험에서 작업물의 수는 30개, 50개, 100개의 세 경우를 가정하였고, 공정시간은 1에서 50 사이의 정수를 무작위로 생성하였다. 또한 대기시간 제약은 , 을 만족하도록 무작위로 생성하였다.
GALS의 대표적인 파라미터로는 모집단 크기, 세대수, 교차 비율, 변이 확률이 있다. 우선 모집단의 크기가 너무 작을 경우 다양한 유전정보를 가지지 못하는 단점이 있다. 반면 모집단의 크기가 너무 클 경우 교차, 지역탐색 등에 소요되는 시간이 커져 해를 구하는데 까지 많은 시간이 소요된다. 따라서 적절한 수의 모집단 크기를 선정하는 것이 중요하고 모집단의 크기는 고려하는 작업수와 관계가 깊으므로 본 연구에서는 모집단의 크기를 (작업 수×k)로 설정하고 1에서 10까지의 k에 대하여 예비 실험을 진행하였다. 알고리즘의 성능과 계산시간의 상충 관계를 고려하여 k를 3으로 설정하였다.
앞서 언급한 바와 같이, 특정 세대의 유전정보가 선택 과정을 통하여 다음 세대로 전달된다. 이 때 진행되는 최대 세대수를 알고리즘의 종료조건으로 활용하며, 따라서 적절한 세대수를 결정해야 한다. 세대수를 너무 크게 잡을 경우, 해를 얻기까지 많은 시간이 소요되고, 세대수를 너무 작게 가져갈 경우 최적해에 근접한 해를 도출하지 못할 가능성이 크다. 기존 문헌을 바탕으로 세대수로는 100, 200, …, 1000을 고려하였고 예비실험을 통해 300을 적정 세대수로 설정하였으며, 교차비율과 변이확률로는 {0.5, 0.7, 1}과 {0.01, 0.05, 0.1, 0.2}에 대하여 예비실험을 진행하여 각각 0.5, 0.2로 설정하였다(Eroglu et al., 2014; Tseng and Lin, 2009).
파라미터가 4종류이고 각각 여러 대안들을 고려하였기 때문에 가능한 조합의 수가 많아 예비실험 결과 데이터가 방대하고 본 논문의 핵심 내용은 아니므로 예비실험결과를 본 논문에 포함하지 않았음을 밝힌다.
5.2 실험세팅
본 연구에서 다루는 생산시스템의 대표적인 파라미터는 작업물의 수, 공정시간, 대기시간 제약이다. 우선, 작업물의 수에 따라 제안된 알고리즘의 성능이 어떻게 변화하는지 살펴보고 혼합정수계획모형으로부터 얻은 해와 비교하기 위해 작업물의 수가 10, 20, 30, 40, 50, 100인 경우를 고려하였다. 또한 대기시간 제약 측면에서 대기시간 제약이 매우 엄격할 경우 no-wait 플로우샵 스케줄링 문제와 유사한 속성을 가지고, 반대로 대기시간 제약이 느슨할 경우 시간제약이 없는 일반 플로우샵 스케줄링 문제와 유사해진다. 따라서 이러한 상황을 모두 고려하기 위하여 아래 <Table 1>과 같이 공정시간의 범위는 고정하고, 세 가지 유형의 대기시간 제약을 고려한다.
<Table 1>에서 실험세팅(1)은 공정시간 대비 대기시간 상한이 작은 즉, 대기시간 제약이 엄격한 경우를 나타낸다. 실험세팅(2)는 공정시간의 상한과 의 상한이 같은 경우를 나타내며, 마지막으로 실험세팅(3)은 대기시간 상한이 공정시간 대비 큰 경우를 나타낸다. 향후 본 장에서는 앞서 언급한 실험세팅(1)~(3)에 대하여 실험을 수행한다.
5.3 휴리스틱 및 지역탐색기법 효과성 검증
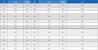
<Table 2>의 3열부터 8열은 초기모집단 구성을 위한 휴리스틱 및 지역탐색 기법이 포함되지 않은 단순 GA(<Table 2>의 GA), 단순 GA에 초기 모집단 구성을 위한 휴리스틱 방법이 추가된 경우(<Table 2>의 GA+H), 그리고 본 논문에서 제안하는 휴리스틱과 지역탐색 기법이 모두 포함된 GALS(<Table 2>의 GALS)의 결과를 보여준다. 앞서 언급한 바와 같이 작업 수 n으로 10, 20, 30, 40, 50, 100이 고려되었고, 각각의 n과 실험세팅 (1)-(3)에서 주어진 범위에 맞도록 공정시간과 대기시간 제약을 무작위로 생성하였다. 실험결과의 신뢰도를 높이기 위하여 각 조합에 대하여 30번의 반복 실험을 수행하였고, <Table 2>는 평균값을 보여준다.
MS는 makespan을 나타내며, CT는 해를 얻을 때까지 걸린 계산시간을 초단위로 나타낸다. 우선 GA와 GA+H를 비교해보면, 초기모집단 구성을 위해 휴리스틱 방법을 사용하면 모든 n에 대하여 makespan을 줄일 수 있음을 확인할 수 있다. 실험세팅 (1), (2), (3)에 대해 n = 100인 경우 makespan이 각각 1.8%, 4.0%, 0.4% 개선되었다. 흥미로운 점은 n이 커짐에 따라 GA+H의 계산시간이 단순 GA에 비해 더 작아짐을 알 수 있다. 이는 단순 GA와 같이 모든 초기해를 무작위로 생성할 경우 교차과정에서 서로 겹치는 작업들이 많이 발생하게 되고(<Figure 3> 참고) 이를 보정하는데 추가적인 계산시간이 필요하기 때문으로 해석할 수 있다. 반면 휴리스틱 기법을 활용하면 비교적 유사한 작업 순서를 갖는 유전자가 많이 생성되고 교차과정에서 겹치는 작업을 처리하는데 필요한 계산시간을 줄일 수 있다.
GALS는 모든 n에 대하여 GA와 GA+H에 비해 더욱 개선된 makespan을 도출함을 알 수 있다. 일례로, n = 100인 경우 실험세팅 (1), (2), (3)에서 각각 GA에 비해 3.7%, 5.2%, 0.7%, GA+H에 비해 각각 2.0%, 1.2%, 0.3% 개선된 makespan을 얻을 수 있다. 다음 절에서 소개되겠지만, GA와 GA+H도 최적해와 비교했을 때 매우 우수한 해를 주기 때문에 GALS를 통한 추가 개선은 큰 의미가 있다고 할 수 있다. 반면, 지역탐색으로 인해 계산시간은 증가함을 알 수 있다. 하지만 n = 100인 경우 평균 계산시간은 299초로 충분히 실용적으로 활용될 수 있다.
5.4 혼합정수계획모형과의 비교를 통한 성능 검증
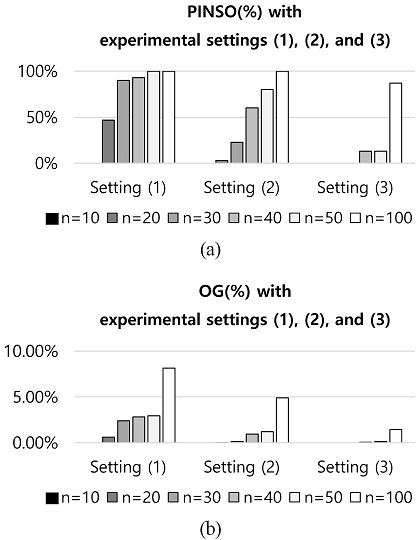
<Table 2>의 9열에서 12열은 혼합정수계획모형을 통해 얻은 해에 대한 결과를 보여준다. 최적해를 얻기 위해 Kim and Lee (2019)에 소개된 혼합정수계획모형을 사용하였고, solver는 Gurobi (Version 9.0.2)를 사용하였다. 또한 최적해를 얻기까지 걸리는 시간에 1시간의 제약을 두었다. 1시간 내에 최적해가 도출된 경우 해당 makespan을 사용하였고, 그렇지 않은 경우 해당 시간까지 도출된 makespan을 활용하였다. 11열의 PINSO(Percentage of the Instances Not Solved to Optimality)는 30개의 인스턴스 중 1시간 내에 최적해를 도출하지 못한 인스턴스의 비율을 의미하며 12열의 OG(Optimality Gap)은 그러한 인스턴스들의 평균 optimality gap(1시간이 경과된 상황에서 solver의 lower bound와 현재 해와의 차이)을 나타낸다. 마지막으로 13열은 본 논문에서 제안한 GALS를 통해 얻은 makespan과 혼합정수계획모형을 통해 얻은 makespan과의 차이를 나타내며, 아래의 수식으로 계산하였다.
- (MS by GALS–MS by MILP)×100 / MS by MILP.
<Table 2>의 결과를 살펴보면, 작업수가 증가함에 따라 혼합정수계획모형을 활용하여 해를 얻는 데까지 걸리는 시간이 실험세팅 (1), (2), (3) 모두에서 급격히 증가함을 알 수 있다. 특히 대기시간 제약이 엄격한 실험세팅 (1)의 경우 작업수가 20개만 되어도 평균 계산시간이 2200초(약 37분)넘게 소요된다. 반면 느슨한 대기시간 제약을 가정한 실험세팅 (3)의 경우 작업수에 대한 계산시간 증가가 비교적 완만함을 알 수 있다. 이러한 특성은 PINSO와 OG으로 이어지며, <Figure 5>와 같이 실험세팅 (1), (2), (3)의 순서로 PINSO와 OG이 전반적으로 감소함을 알 수 있다.
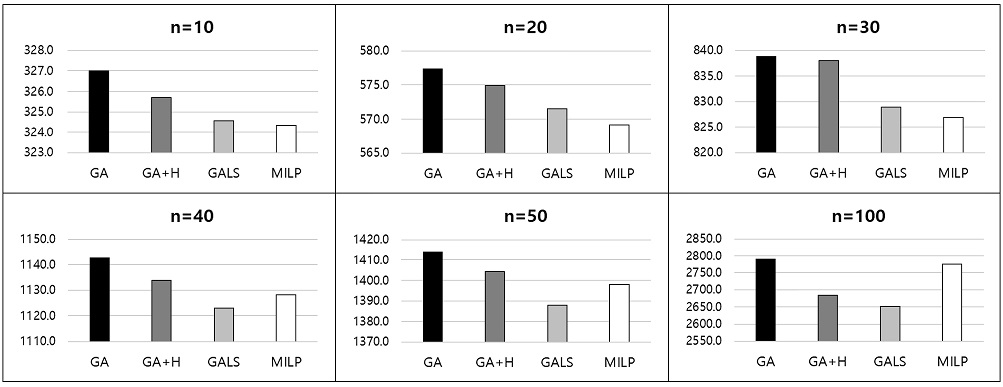
반면 본 논문에서 제안된 GALS의 계산시간은 실험세팅 (1)-(3)에 큰 영향을 받지 않음을 알 수 있다. GALS를 통해 얻은 해와 혼합정수계획모형을 통해 얻은 해를 비교해보면, 모든 경우에 대해 makespan의 차이가 1% 이내임을 <Table 2>에서 확인할 수 있다. 또한 앞서 언급한 바와 같이 작업수가 증가함에 따라 혼합정수계획모형을 통해 1시간 이내에 최적해를 얻지 못하는 경우가 빈번히 발생하고 그러한 경우에는 오히려 GALS를 통해 더 좋은 makespan을 얻을 수 있다. 일례로 실험세팅 (2)에 대해 GA, GA+H, GALS로부터 얻은 makespan과 혼합정수계획모형을 통해 얻은 makespan을 비교하면 아래 <Figure 6>과 같다(실험세팅 (1)과 (3)의 결과도 유사한 양상을 보임).
<Figure 6>에서 살펴볼 수 있듯이, GALS를 통해 GA 및 GA+H에 비해 개선된 makespan을 얻을 수 있으며, 혼합정수계획모형을 통해 얻은 해와 큰 차이가 없음을 알 수 있다. 예를 들어, 작업수가 10일 때 모든 인스턴스들에 대해 1시간 내에 혼합정수계획모형을 통해 최적해를 얻을 수 있으며, GALS를 통한 해와 최적해의 차이는 평균 0.15%이다. 작업수가 40이상이면, 1시간의 시간제한을 통해 혼합정수계획모형으로 얻은 해보다 오히려 좋은 makespan을 얻을 수 있음을 확인할 수 있다. 일례로, 작업수가 100인 경우 GALS를 통한 해와 혼합정수계획모형을 통해 얻은 해와의 차이는 평균 -3.92%로 GALS를 통해 더 좋은 makespan을 얻을 수 있다.
요약하면 혼합정수계획모형의 경우 실험세팅에 크게 영향을 받으며 작업수가 증가함에 따라 계산시간이 빠르게 증가하여 현실적인 문제에 대해 주어진 시간 내에 최적해를 제공하지 못하는 경우가 빈번히 발생함을 알 수 있다. 반면 본 논문에서 제안한 GALS의 경우 실험세팅에 관계없이 빠른 시간 내에 우수한 해를 도출함을 알 수 있다.
5.5 추가실험
앞서 본장 4절에서 소개한 바와 같이 작업수가 큰 경우 계산시간 제한을 1시간으로 하면 대부분의 경우 혼합정수계획모형을 통해 최적해를 얻지 못함을 알 수 있다. 따라서 계산시간 제한을 12시간으로 늘려 추가 비교실험을 진행한다. 모든 실험세팅 (1)-(3)에 대하여 추가실험을 진행하지는 않았으며, 앞 절에서 소개한 바와 같이 비교적 혼합정수계획모형의 평균 계산시간이 짧은 실험세팅(3)을 대상으로 하였음을 밝힌다.
앞서 언급한 바와 같이 실험세팅 (3)에 대하여 최적해를 위한 계산시간 제한을 12시간으로 늘리고 작업수 또한 늘려 (n = 150,200) 각 n에 대하여 10개의 인스턴스를 무작위로 생성하여 반복 실험을 진행하였다. <Table 3>의 결과와 같이 n이 큰 경우 계산시간 제한을 12시간으로 늘려도 모든 경우에 최적해를 얻을 수 없었다. n이 300인 경우도 시도하였으나 메모리 부족(out of memory)으로 Gurobi가 중단되었음을 밝힌다. n이 150인 경우 GALS의 평균 계산시간은 1454.07초로 약 24분 정도가 소요되며 12시간의 계산을 통해 Gurobi로부터 얻은 해보다 2.88% 더 좋은 makespan을 도출함을 알 수 있다. n이 200인 경우 GALS의 평균 계산 시간은 4856.27초로 약 80분 정도가 소요되며 12시간의 계산을 통해 Gurobi로부터 얻은 해보다 2.68% 좋은 makespan을 얻을 수 있었다. 또한 GA+H의 경우 매우 짧은 계산시간 내에 비교적 우수한 해를 도출함을 알 수 있고, 따라서 매우 짧은 계산시간이 요구되는 상황에서는 충분히 경쟁력 있는 대안으로 활용될 수 있음을 알 수 있다.
6. 결 론
본 논문에서는 중첩 대기시간 제약을 갖는 플로우샵 스케줄링을 위해 유전알고리즘 기반의 스케줄링 방법을 제안하였다. 본 논문에서 제안된 GALS는 초기모집단 구성을 위한 휴리스틱 방법과 해 개선을 위한 지역탐색 기법을 포함하며, 실험을 통해 해당 방법들이 제안된 스케줄링 알고리즘의 성능을 향상시킴을 보였다. 또한 혼합정수계획모형을 통해 얻은 해와의 비교를 통해 제안된 스케줄링 방법이 빠른 시간 내에 최적해에 근사한 해를 도출함을 확인하였다. 실험결과의 타당성을 높이기 위하여 다양한 실험세팅으로 실험을 진행하였으며, 제안된 방법이 최적화 기법과 달리 실험환경에 크게 영향을 받지 않고 안정적인 성능을 보임을 확인하였다. 작업수가 작은 경우 최적해와 비교하여 1%이내의 차이를 보였으며, 작업수가 커질 경우 시간제한을 두고 혼합정수계획모형을 통해 얻은 해보다 오히려 좋은 해를 얻을 수 있음을 확인하였다.
추가 연구로는 크게 두 가지 방향을 생각해 볼 수 있다. 첫째로, 본 연구의 결과를 확장하여 보다 일반적인 생산시스템에 적용해 보는 것이다. 예를 들어, 중첩 대기시간 제약이 있는 m-설비 플로우샵 스케줄링 문제 또는 잡샵 스케줄링 문제에 적용해 볼 수 있다. 또 다른 방향으로는 계산시간 단축과 최적해와의 차이를 줄이기 위한 알고리즘 성능 개선에 관한 연구가 있다. 구체적으로 유전자 표현방식, 교차, 변이 등의 방법을 개선하거나 더욱 효율적인 지역탐색 기법의 제안 등을 고려해 볼 수 있다.
Acknowledgments
본 연구는 충남대학교 학술연구비에 의해 지원되었음.
References
-
An, Y.-J., Kim, Y.-D., and Choi, S.-W. (2016), Minimizing makespan in a two-machine flowshop with a limited waiting time constraint and sequence-dependent setup times, Computers & Operations Research, 71, 127-136.
[https://doi.org/10.1016/j.cor.2016.01.017]

-
Attar, S. F., Mohammadi, M., Tavakkoli-Moghaddam, R., and Yaghoubi, S. (2014), Solving a new multi-objective hybrid flexible flowshop problem with limited waiting times and machine–sequence-dependent set-up time constraints, International Journal of Computer Integrated Manufacturing, 27(5), 450-469.
[https://doi.org/10.1080/0951192X.2013.820348]

-
Blazewics, J., Breit, J., Formanowicz, P., Kubiak, W., and Schmidt, G. (2001), “euristic algorithms for two-machine flowshop with limited machine availability, Omega, 29(6), 599-608.
[https://doi.org/10.1016/S0305-0483(01)00048-2]

-
Bouquard, J.-L. and Lente, C. (2006), Two-machine flow shop scheduling problems with minimal and maximal delays, Quarterly Journal of Operations Research, 4, 15-28.
[https://doi.org/10.1007/s10288-005-0069-7]

-
Cheng, M., Tadikamalla, P. R., Shang, J., and Zhang, S. (2014), Bicriteria hierarchical optimization of two-machine flow shop scheduling problem with time-dependent deteriorating jobs, European Journal of Operational Research, 234(3), 650-657.
[https://doi.org/10.1016/j.ejor.2013.09.033]

-
Croce, F. D., Grosso, A., and Salassa, F. (2014), A matheuristic approach for the two-machine total completion time flow shop problem, Annals of Operations Research, 213(1), 67-78.
[https://doi.org/10.1007/s10479-011-0928-x]

-
Eroglu, D. Y., Ozmutlu, H. C., and Ozmutlu, S. (2014), Genetic algorithm with local search for the unrelated parallel machine scheduling problem with sequence-dependent set-up times, International Journal of Production Research, 52(19), 5841-5856.
[https://doi.org/10.1080/00207543.2014.920966]

-
Fondrevelle, J., Oulamara, A., and Portmann, M.-C. (2006), “Permutation flowshop scheduling problems with maximal and minimal time lags, Computers & Operations Research, 33(6), 1540-1556.
[https://doi.org/10.1016/j.cor.2004.11.006]

-
Hamdi, I. and Loukil, T. (2015), Minimizing total tardiness in the permutation flowshop scheduling problem with minimal and maximal time lags, Operational Research, 15(1), 95-114.
[https://doi.org/10.1007/s12351-014-0166-5]

-
Joo, B.-J. and Kim, Y.-D. (2009), A branch-and-bound algorithm for a two-machine flowshop scheduling problem with limited waiting time constraints, Journal of the Operational Research Society, 60, 572-707.
[https://doi.org/10.1057/palgrave.jors.2602598]

-
Ju, F., Li, J., and Horst, J. A. (2017), Transient analysis of serial production lines with perishable products : Bernoulli reliability model, IEEE Transactions on Automatic Control, 62(2), 694-707.
[https://doi.org/10.1109/TAC.2016.2572119]

-
Kim, H.-J. and Lee, J.-H. (2019), Three-machine flow shop scheduling with overlapping waiting time constraints, Computers & Operations Research, 101, 93-102.
[https://doi.org/10.1016/j.cor.2018.06.009]

- Lee, G.-C. (2006), Scheduling methods for a hybrid flowshop with dynamic order arrival, Journal of the Korean Institute of Industrial Engineers, 32(4), 373-381.
- Moon, B.-R. (2003), Genetic Algorithm, Dooyang-Sa, Seoul, Korea.
-
Nawaz, M., Enscore, E. E., and Ham, I. (1983), A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem, Omega, 11(1), 91-95.
[https://doi.org/10.1016/0305-0483(83)90088-9]

-
Rajendran, C. and Ziegler, H. (2004), Ant-colony algorithms for permutation flowshop scheduling to minimize makespan/total flowtime of jobs, European Journal of Operational Research, 155, 426-438.
[https://doi.org/10.1016/S0377-2217(02)00908-6]

-
Tasgetiren, M. F., Liang, Y.-C., Sevkli, M., and Gencyilmaz, G. (2007), A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem, European Journal of Operational Research, 177(3), 1930-1947.
[https://doi.org/10.1016/j.ejor.2005.12.024]

-
Tseng, L.-Y. and Lin, Y.-T. (2009), A hybrid genetic local search algorithm for the permutation flowshop scheduling problem, European Journal of Operational Research, 198(1), 84-92.
[https://doi.org/10.1016/j.ejor.2008.08.023]

-
Vallada, E. and Ruiz, R. (2011), A genetic algorithm for the unrelated parallel machine scheduling problem with sequence dependent setup times, European Journal of Operational Research, 211(3), 612-622.
[https://doi.org/10.1016/j.ejor.2011.01.011]

-
Wang, J., Hu, Y., and Li, J. (2010), Transient analysis to design buffer capacity in dairy filling and packing production lines, Journal of Food Engineering, 98(1), 1-12.
[https://doi.org/10.1016/j.jfoodeng.2009.11.009]

- Woo, H.-S., Yim, D.-S., and Lee, W.-K. (1996), A heuristic algorithm for mean flowtime minimization in permutation flowshop scheduling, Journal of the Korean Institute of Industrial Engineers, 22(1), 115-127.
-
Wu, C.-C., Yin, Y., and Cheng, S.-R. (2013), Single-machine and two-machine flowshop scheduling problems with truncated position-based learning functions, Journal of the Operational Research Society, 64, 147-156.
[https://doi.org/10.1057/jors.2012.46]

-
Yang, D.-L. and Chern, M.-S. (1995), A two-machine flowshop sequencing problem with limited waiting time constraints, Computers & Industrial Engineering, 28(1), 63-70.
[https://doi.org/10.1016/0360-8352(94)00026-J]

-
Yu, T.-S., Kim, H.-J., and Lee, T.-E. (2017), Minimization of waiting time variation in a generalized two-machine flowshop with waiting time constraints and skipping jobs, IEEE Transactions on Semiconductor Manufacturing, 30(2), 155-165.
[https://doi.org/10.1109/TSM.2017.2662231]

이준호 : 한국과학기술원 산업및시스템공학과에서 2008년 학사, 2013년 박사학위를 취득하였다. 삼성전자 책임연구원, University of Wisconsin-Madison 연구원, 건국대학교 경영학과 조교수 등을 역임하고 2020년부터 충남대학교 경영학부 조교수로 재직하고 있다. 주 연구분야는 생산 시스템의 모델링 및 스케줄링이다.
유태선 : 한국과학기술원 산업및시스템공학과에서 2012년 학사, 2017년 박사학위를 취득하였다. 한국과학기술원 연구원, New York University 연구원 등을 역임하고 2020년부터 부경대학교 시스템경영공학부 조교수로 재직하고 있다. 주 연구분야는 생산 시스템 스케줄링 및 최적화이다.
박경수 : 연세대학교 컴퓨터산업공학과와 화학공학과에서 2008년 학사를 취득하고, 한국과학기술원 산업및시스템공학과에서 2014년 박사학위를 취득하였다. 국방기술품질원 선임연구원, University of Wisconsin-Madison 연구원, 동아대학교 산업공학과 조교수 등을 역임하고, 현재 부산대학교 경영학과 조교수로 재직 중이다. 주 연구분야는 시스템 모델링 및 최적화이다.