최적 큐빗 할당을 위한 정수계획 모형
© 2021 KIIE
Abstract
A qubit allocation problem is to find an assignment of logical qubits in a quantum algorithm to the physical qubits of a quantum computing device. The physical qubits are often configured in a coupling map, which is a directed graph that represents communication relationship between adjacent physical qubits. A proper qubit allocation satisfies all logical qubit communication relationship in a quantum circuit by conforming to the coupling map restriction. To find the proper qubit allocation, we often need to change the quantum circuit by using a set of circuit transformations, which include reversal, bridge, and swap. Such a transformation results in the quantum circuit with newly added quantum gates and subsequenlty causes extra quantum errors. In this study, we propose an integer programming model that minimizes the sum of the quantum costs of the circuit transformation. In our model, all three circuit transformations are considered. Moreover, we present the results of the computational experiment in which our model is compared with heuristic procedures from previous studies.
Keywords:
Qubit Allocation, Quantum Computing, Integer Programming, Coupling Map, Quantum Circuit1. 서 론
2017년, IBM은 세계 최초 양자컴퓨팅 유료 시스템인 “IBM Q”를 공개한다. 공개 당시의 디지털 컴퓨터로 수행할 수 없던 고준위 물리 시스템 시뮬레이션의 연산이 IBM의 양자컴퓨터로는 가능하다고 발표한다(Castelvecchi, 2017). 또 다른 양자컴퓨터 기업인 D-wave는 제약식이 없는 이차 최적화 문제를 해결하기 위해, 디지털 컴퓨터를 사용한 연산 시간보다 약 26,000배 빠른 양자컴퓨터를 소개한다(King et al., 2019). 또한, 비슷한 시기에 Google은 디지털 컴퓨터를 통해 약 10,000년 정도의 연산 시간이 소요되는 문제를 Google의 양자컴퓨터를 사용할 경우 약 3분 20초 정도에 수행할 수 있다는 결과를 발표한다(Murgia et al., 2019). 이들 최근 연구들은 양자 컴퓨터 알고리즘을 사용하면 특정 문제들의 해를 찾기 위한 연산 시간을 획기적으로 줄일 수 있음을 보여준다.
양자 컴퓨팅에 관한 연구는 양자 컴퓨터 기기 자체의 정확도를 높이는 하드웨어에 관한 연구와 새로운 양자 컴퓨팅 계산 알고리즘을 통해 연산 시간을 줄이는 소프트웨어에 관한 연구로 나뉜다. 양자 컴퓨팅 알고리즘(quantum computing algorithm)은 양자 컴퓨터의 특수한 구조로 인해 고전 알고리즘과 다른 계산 방식이 요구된다. 이러한 차이점 때문에 기존 디지털 컴퓨터로 해를 구하기 어려운 문제들을 양자컴퓨터로 해결하기 위해서는 양자컴퓨터의 구조적 특성을 이용한 양자 컴퓨팅 알고리즘에 관한 연구가 필수적이다(Montanaro, 2016).
양자 컴퓨팅 알고리즘은 큐빗(qubit)을 계산의 기본 단위로 한다. 큐빗은 0과 1 두 개의 상태를 동시에 저장하는 중첩(superposition)이라는 특성과, 큐빗 각각의 독립적 양자 상태의 조합으로는 표시할 수 없는 두 개 이상 다수 큐빗의 양자 상태를 나타내는 얽힘(entanglement)이라는 특성을 가진다. 하나의 큐빗의 상태는 벡터로 표현할 수 있으며 벡터 성분의 제곱은 각 상태가 관측될 확률을 의미한다. 중첩이라는 특성으로 인해 하나의 큐빗은 고전 컴퓨터의 비트(bit)와 다르게 0과 1 두 상태를 동시에 저장하는 것이 가능하다. 또한, 한 큐빗의 상태에 따라 여러 개의 큐빗의 상태가 결정지어지는 얽힘이라는 특성을 통해 중첩 현상 만으로 나타낼 수 없는 상태 또한 저장할 수 있다.이 두 특성으로 인해 양자 컴퓨팅 알고리즘은 고전 컴퓨팅 알고리즘보다 연산 시간이 빠르고 처리할 수 있는 데이터의 크기가 더 크다는 이점을 가진다. 이러한 양자 컴퓨팅 알고리즘의 실용화 및 실제 연산 시간 단축을 위해 실제 양자 컴퓨팅 기기와 정보 입력 체계에 관한 연구가 진행되고 있다(Balensiefer et al., 2005).
위에서 제시한 양자 컴퓨팅 알고리즘의 특성을 활용하여 수송 문제, 잡샵 스케줄링 문제(job shop scheduling), 경로 최적화 문제 등의 조합 최적화 문제들을 해결하고자 하는 연구가 진행 중이다. 앞에서 언급된 최적화 문제들은 NP 난해 문제(NP-complete problem)임이 알려진 문제들로, 양자 컴퓨팅 알고리즘을 활용하면 더 적은 계산 시간을 이용해 더 좋은 해를 구할 수 있을 것으로 전망된다. 예시로, 한 연구는 잡샵 스케쥴링 문제를 해결하기 위해 고전 컴퓨팅 알고리즘과 양자 컴퓨팅 알고리즘을 혼합한 알고리즘을 제시한다. 고전 컴퓨팅 알고리즘을 통해 완화된 혼합 선형계획 모형의 해를 구한다. 이후 양자 컴퓨팅 알고리즘을 통해 그 해가 본 문제에서 가능한 정수 해인지 검증한다. 중첩과 얽힘을 이용하여 초기 큐빗들의 양자 상태의 벡터가 해의 벡터와 동일하게 만든다. 이후 목적식과 제약식에 대한 라그랑지안 형태인 양자 게이트를 거친 후 큐빗들을 관측해 가능해 여부를 판단한다. 가능해가 아닌 경우 절단 평면을 추가하고 본 과정을 반복한다(Ajagekar et al., 2020).
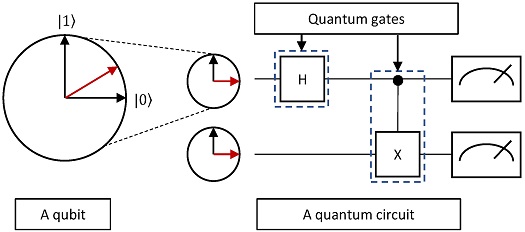
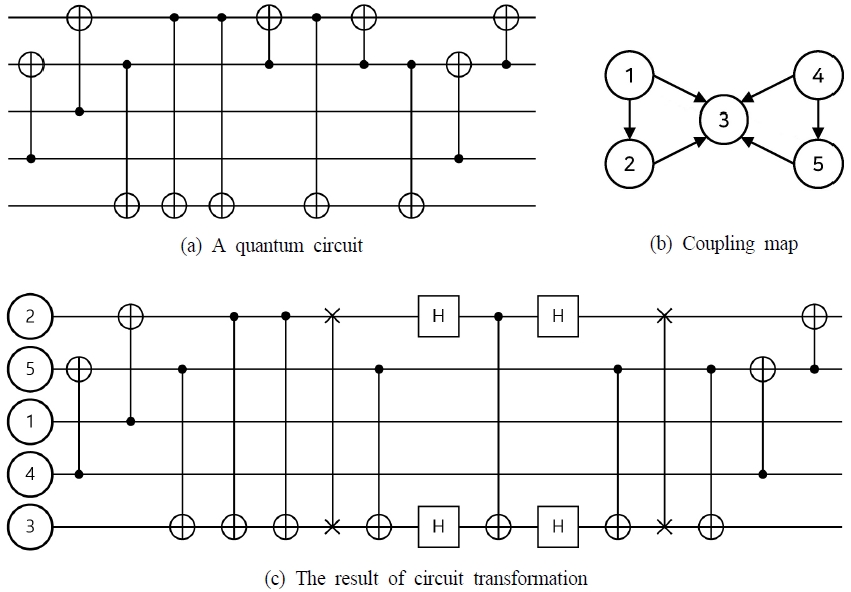
게이트 기반 양자 컴퓨팅 알고리즘은 입력된 큐빗의 상태를 변화시킨 후 그 큐빗들을 관측하는 과정으로 진행된다. 큐빗들의 상태 변화는 양자 게이트(quantum gate)를 이용하여 처리한다. 즉, 게이트 기반 양자 컴퓨팅 알고리즘은 각 큐빗에 일련의 양자 게이트를 적용하여 원하는 양자 상태로 변화시키는 과정을 수행한다. 각 큐빗에 적용하는 양자 게이트 및 그 순서를 표현하기 위해 양자 회로(quantum circuit)를 이용한다. 양자 회로는 큐빗을 나타내는 가로줄과 양자 게이트들로 구성되며 양자 회로를 통해 양자 컴퓨팅 알고리즘의 최종 양자 상태를 계산할 수 있다. <Figure 1>은 큐빗과 양자 회로의 관계를 나타낸다.
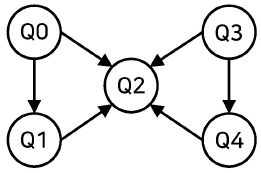
현존하는 IBM의 게이트 기반 양자 컴퓨터는 결합 구조도(coupling map)라는 물리적 제약 조건을 가진다. 결합 구조도는 큐빗 간 얽힘이 가능한지 나타내는 유향 그래프이다. 결합 구조도는 노드(node)와 아크(arc)로 표현되며, 노드는 양자 컴퓨터의 큐빗, 아크는 그 아크로 연결된 두 노드의 큐빗을 얽힘이 가능함을 나타낸다. 결합 구조도의 물리적 특성으로 인해 양자 회로의 제어된 게이트들의 제어 큐빗(control qubit)과 목표 큐빗(target qubit)이 결합 구조도의 아크의 머리 큐빗과 꼬리 큐빗에 각각 대응되어야 한다. 모든 제어된 게이트에 대해 이상의 조건을 만족하게 실제 양자 컴퓨터의 결합 구조도의 큐빗과 양자 회로의 큐빗을 대응시키는 문제를 큐빗 할당 문제(qubit allocation problem)라고 한다(Siraichi et al., 2018).
결합 구조도의 아크의 개수는 한정적이므로 본래의 양자 회로의 큐빗 할당 문제를 푸는 것은 일반적으로 불가능하다. 따라서 양자 회로에 일련의 양자 게이트들을 추가시켜 양자 회로 상의 제어 큐빗과 목표 큐빗의 관계들을 변형하는 과정을 거친다. 이러한 변형 과정에는 제어 큐빗과 목표 큐빗의 관계를 역으로 바꾸는 반전 변환(reversal transformation), 하나의 제어된 게이트를 두 개의 제어된 게이트로 나누는 연결 변환(bridge transformation), 실제 양자 컴퓨터의 큐빗에 대응된 양자 회로의 큐빗들을 서로 바꾸는 교환 변환(swap transformation)이 있다. 이러한 변환들은 양자 게이트를 추가하는 방식으로 진행된다. 양자 게이트의 추가는 양자 회로의 정확도를 감소시킨다. 정확도의 감소분을 정성적으로 표현하기 위해 양자 비용(quantum cost)이라는 척도를 사용하며, 각 변환은 추가되는 양자 게이트들의 정확도에 따라 특정한 양자 비용을 가진다. 양자 알고리즘의 개발에 있어 양자 회로에 추가되는 양자 게이트 수를 줄이고 양자 회로의 정확도를 최대로 유지하기 위해, 양자 비용의 합을 최소화하는 큐빗 할당 문제 해결의 중요성을 가진다.
이 연구에서는 큐빗 할당 문제를 해결하기 위한 정수계획 모형을 제시하고 그 결과를 기존의 휴리스틱과 비교한다. 정수계획 모형을 설계하기 위해 큐빗 할당 문제를 반전 변환과 연결 변환을 이용해 제어된 게이트의 제어 큐빗과 목표 큐빗을 바꾸는 문제와 제어된 게이트 간 교환 변환을 통해 실제 양자컴퓨터의 큐빗과 양자 회로의 큐빗의 대응 관계를 바꾸는 문제로 분류한다. 모델의 성능과 적합성을 검증하기 위해 기존의 휴리스틱 알고리즘과 수리적 모델이 실험을 진행한 양자 회로에 대해 실험을 진행하며 계산 시간과 정확도를 비교한다.
2. 최근 연구 동향
큐빗 할당 문제에 관한 초기 연구는 직선으로 표현되는 1차원의 결합 구조도에 교환 변환만을 이용하여 큐빗을 할당하는 것을 목적으로 한다. 이후 격자 형태의 결합 구조도에 큐빗을 할당하고자 하는 연구가 진행되며, 반전 변환도 사용하는 연구가 제시된다. 최근에는 3차원 이상의 결합 구조도에서의 큐빗 할당 문제와, 반전 변환, 연결 변환, 교환 변환을 모두 사용하는 큐빗 할당에 관한 연구가 진행되고 있다.
Kole et al.(2016), Wille et al.(2014) 등은 1차원의 결합 구조도에서의 큐빗 할당 문제에 관한 연구이다. 1차원의 결합 구조도에서의 큐빗 할당 문제는 결합 구조도를 나타내는 직선 형태의 그래프에서 제어 큐빗과 목표 큐빗 간 거리가 1이 되어야 한다는 제약 조건을 가진다. 이를 만족하기 위해 교환 변환을 이용하여 회로를 변형한다. 이 과정에서 사용되는 교환 변환의 수를 양자 비용으로 정의한다. Kole et al.(2016)은 인접한 두 개 제어된 게이트 쌍에 대하여 각 통제된 게이트의 통제 큐빗과 목표 큐빗의 관계에 따라 상황을 분류하고, 각 경우에 대한 양자 비용을 계산해 그 합을 최소로 하는 휴리스틱을 제시한다. Wille et al.(2018)은 양자 회로의 교환 변환의 수가 최소가 되는 큐빗 순서를 우선 정하는 전역 배치 후, 각 제외된 게이트를 제약 조건에 맞추기 위해 발생한 교환 변환을 상쇄해 양자 회로 이후 큐빗 순서를 지역 배치하여 근사해를 구한다.
Alfailakawi et al.(2016), Lye et al.(2015), Ruffinelli et al.(2017), Shrivastwa et al.(2015), Shafaei et al.(2014) 등은 2차원의 격자 형태의 결합 구조도에서 제어 큐빗과 목표 큐빗이 서로 이웃할 수 있게 큐빗을 할당한다. 이들 연구는 2차원의 결합 구조도는 직사각형이며 결합 구조도 상의 큐빗 수는 양자 회로의 큐빗 수보다 크다고 가정한다. 큐빗 할당을 위하여 교환 변환을 사용하며, 발생하는 교환 변환의 횟수를 양자 비용으로 정의한다.
각 연구 내용은 다음과 같다. Alfailakawi et al.(2016)은 양자 회로에 포함되지 않은 게이트들을 통해 상호 작용 그래프(interaction graph)를 형성하고 이를 활용한 하모니 탐색 알고리즘을 제시한다. Lye et al.(2015)은 1차원과 2차원의 결합 구조도에 대하여 양자 회로의 큐빗들과 결합 구조도의 큐빗 간 대응 관계를 상태로 정의한다. 이후 상태를 노드로 하고, 1번의 반전 변환을 통해 서로의 상태가 될 수 있는 노드 사이가 아크로 연결된 그래프를 형성한다. 이후 그래프상 각 노드의 양자 비용을 계산해 최종 큐빗 할당의 양자 비용이 최소가 되게 하는 휴리스틱을 제시한다. Ruffinelli et al.(2017)은 필요한 반전 변환의 수와 큐빗 할당 후 제어 큐빗과 목적 큐빗 간 거리를 최소화하는 다목적 최적화 모형을 제시한다. Shrivastwa et al.(2015)은 다양한 형태의 결합 구조도에 대하여 휴리스틱을 진행하며, 양자 회로의 큐빗을 결합 구조도에 할당한 후 이후 통제된 게이트들이 제약 조건을 만족하게 반전 변환을 포함한다. Shafaei et al.(2014)은 큐빗 할당 여부에 따른 이진 변수에 대한 혼합 정수 모형을 제시하며 그 해를 구하는 휴리스틱을 제시한다. Zulehener et al.(2019)은 양자 회로를 큐빗이 겹치지 않는 단위로 나눈 후 단위별로 큐빗 할당을 진행하는 휴리스틱을 제시하고 실제 양자컴퓨터의 결합 구조도에 대하여 그 성능을 검증한다.
이후 육면체 형태의 3차원의 결합 구조도와 더 복잡한 구조를 가진 결합 구조도에서 큐빗 할당 문제에 관한 연구가 진행된다. Kole et al.(2018)은 1차원, 2차원과 3차원의 결합 구조도에 대해 큐빗 간 거리를 정의하고 그 거리가 최소가 되도록 양자 회로의 큐빗을 결합 구조도에 전역 할당한 후 제어된 게이트 별로 제약 조건을 만족하게 큐빗 할당을 바꾸는 휴리스틱을 제안한다. Farghadan et al.(2017)은 큐빗 간 제어된 게이트의 수로 큐빗과 큐빗 간 사이에 대한 중요도를 계산한 후 중요도에 따라 2차원의 결합 구조도 상에 양자 회로의 큐빗을 배열하는 휴리스틱을 제시한다. 이후 Farghadan et al.(2019)은 Farghadan et al. (2017)을 기반으로 3차원의 결합 구조도 상에 양자 회로의 큐빗을 배열하는 휴리스틱을 제안한다.
Siraichi et al.(2018)은 연결 변환, 반전 변환, 교환 변환을 모두 이용하여 큐빗 할당 문제를 해결한다. 각 변환의 양자 비용을 임의의 정수로 가정하여 양자 비용의 합을 최소화하는 큐빗 할당을 찾는 것을 목적으로 한다. 이 문제의 최적해를 구하기 위해 동적 할당 계획법을 사용하며, 시간 단축을 위한 새로운 휴리스틱 방법론을 제시한다. 이 연구에서는 제시하는 휴리스틱의 성능 검증을 위해 Revlib(http://www.informatik.uni-bremen.de/rev_lib/)에서 제공하는 양자 이진 함수 회로에 대한 큐빗 할당의 양자 비용을 연구의 모형과 기존의 휴리스틱들과의 비교한다.
3. 배경 지식 및 문제 설명
3.1 양자 회로
양자 컴퓨팅의 기본 단위는 큐빗으로, 0과 1 둘 중 하나의 상태만 가질 수 있던 디지털 컴퓨터의 비트와 달리 큐빗은 두 사이 상태에서 존재한다. 양자 상태(quantum state, |Ψ>)는 복소수 α, β를 성분으로 하는 벡터로 표현된다 (). 벡터의 계수를 진폭(amplitude)이라 하며, 진폭의 절댓값의 제곱인 |α|2, |β|2은 각각 상태 0, 1이 관측될 확률을 의미한다. 또한, 진폭의 절댓값의 합은 1을 만족하여야 한다(|α|2+|β|2=1). 양자 상태는 이후 관측(measurement)을 통해 둘 중 하나의 상태로 결정된다.
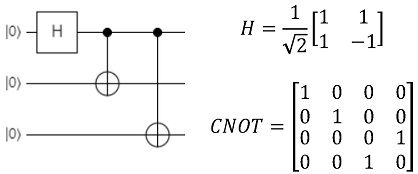
이러한 양자 상태는 양자 게이트에 의해 변한다. 양자 게이트는 복소수 성분의 유니타리 행렬(unitary matrix)로 표현되며, 양자 게이트를 지난 후 양자 상태는 양자 게이트를 나타내는 행렬에 양자 상태 벡터를 곱해서 구할 수 있다. 양자 게이트는 하나의 큐빗에 적용되는 단일 큐빗 게이트와 두 개 이상의 큐빗에 적용되는 다중 큐빗 게이트로 나뉘며, 다중 큐빗 게이트에 제어된 게이트가 포함된다. 제어된 게이트는 제어 큐빗의 상태가 1일 때 목표 큐빗의 상태를 변화시킨다. 제어된 게이트 중 하나인 CNOT 게이트는 제어 큐빗이 1일 때 목표 큐빗의 상태가 0이면 1로 바꾸며, 1이면 0으로 바꾼다. Bareno et al.(1995)는 모든 다중 큐빗 게이트를 단일 큐빗 게이트와 CNOT 게이트의 조합으로 표현할 수 있음을 보인다. <Figure 2>는 양자 회로와 양자 게이트의 예시로 하다마드 게이트(Hadamard gate)라는 단일 큐빗 게이트와 두 개의 CNOT 게이트로 구성되어 있다.
3.2 양자컴퓨터와 결합 구조도
게이트 기반 양자 컴퓨터는 결합 구조도라는 물리적 특성을 가진다. 결합 구조도는 큐빗들을 꼭지점으로 하는 유향 그래프로 나타낼 수 있다. 양자 회로로 표현된 양자 알고리즘을 실제로 구현하기 위해서 결합 구조도 상의 큐빗들에 대해 거치는 양자 게이트를 순서대로 입력해야 한다. 단일 큐빗 게이트는 결합 구조도 상의 임의의 큐빗에 적용할 수 있지만 제어된 게이트의 경우 그 제어 큐빗과 목표 큐빗이 각각 결합 구조도 상의 아크의 꼬리와 머리에 위치해야 한다. 제어 큐빗이 두 개 이상인 게이트의 경우 단일 큐빗 게이트와 CNOT 게이트의 조합으로 표현 가능하므로 그 CNOT 게이트들이 각각 결합 구조도의 조건을 만족해야 한다.
3.3 큐빗 할당 문제
큐빗 할당 문제란 실제 양자컴퓨터의 결합 구조도에 양자 회로의 큐빗을 할당한 후, 결합 구조도 제한 조건에 어긋나게 하지 않기 위해 회로에 변환을 가하거나 게이트를 추가시킬 때 발생하는 양자 비용을 최소화하는 문제다. 양자 회로를 변형하는 변환은 반전 변환, 연결 변환, 교환 변환으로 반전 변환은 제어 큐빗과 목표 큐빗을 서로 바꾸는 변환이다. 연결 변환은 제어 큐빗과 목표 큐빗 사이에 다른 큐빗을 추가하는 변환이다. 마지막으로, 교환 변환은 실제 결합 구조도에 대응된 두 큐빗을 바꾸는 변환이다(Siraichi et al., 2018).
각 변환은 특정한 양자 비용을 가지고 있으며, 양자 비용의 합은 각 연산의 횟수에 선형적으로 비례한다고 가정한다. 실제 양자 컴퓨터의 결합 구조도와 양자 회로의 제어된 게이트의 순서와 각 제어된 게이트의 제어 큐빗과 목표 큐빗의 정보는 주어진다고 가정한다. 양자 회로 변환은 실제 양자 컴퓨터의 결합 구조도에서 근접한 큐빗에서만 이루어지며 양자 회로의 큐빗은 각각 하나의 결합 구조도 상의 큐빗에 대응된다.
이 연구에서는 주어진 양자 회로와 실제 양자 컴퓨터의 결합 구조도에 대해 각 CNOT 게이트들이 결합 구조도의 조건을 만족시키며 최소의 양자 비용을 가지는 큐빗들 간의 대응 관계와 양자 회로 변환을 구하는 것을 목적으로 한다. 이를 수리 모형으로 모델링하기 위해 다음의 사항들을 가정한다.
- 가정 1. 주어진 양자 회로는 단일 큐빗 게이트와 CNOT 게이트로 구성된다.
- 가정 2. 각 변환은 일정한 양자 비용을 가지며 양자 비용의 총량은 각 변환의 양자 비용과 횟수의 곱의 합으로 계산한다.
- 가정 3. 실제 양자 컴퓨터의 큐빗 관측 에러 등 결합 구조도를 제외한 다른 기기적 특성은 양자 비용에 영향을 주지 않는다.
이 연구에서는 큐빗 할당 문제의 수리적 모델링을 위하여 본 문제를 두 개의 문제로 구성한다. 첫 번째 문제는 제어된 게이트 간 교환 변환의 횟수를 최소화하는 문제로 교환 변환을 통해 각 제어된 게이트에서 양자 회로의 큐빗들과 결합 구조도의 큐빗들 간의 대응 관계를 결정한다.
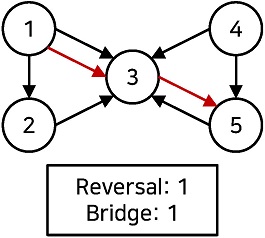
두 번째 문제는 반전 변환과 연결 변환 횟수를 최소화하는 문제로 구성한다. 반전 변환은 제어 큐빗과 목표 큐빗을 서로 바꾸어 제어된 게이트의 제어 큐빗과 목표 큐빗에 대응되는 결합 구조도의 아크의 방향을 반대로 바꾸는 역할을 하며, 연결 변환은 제어 큐빗과 목표 큐빗 간 아크의 수를 증가시키는 역할을 한다. 이를 토대로 반전 변환과 연결 변환 횟수를 최소화하는 문제는 비유향화 된 결합 구조도의 네트워크 최소 비용 유량 문제(minimum cost network flow)로 생각할 수 있다. <Figure 5>는 네트워크 비용 유량 문제 예시로, 결합 구조도 상에서 목표 큐빗이 큐빗 5이고 제어 큐빗이 큐빗 1인 경우, 아크 (3, 5)가 최단 경로에 포함되고 실제 결합 구조도는 아크 (5, 3)으로 포함하므로 반전 변환이 한 번 필요하며 큐빗 1과 큐빗 5 사이에 큐빗 3을 포함하므로 연결 변환이 1번 필요하다.
큐빗 할당을 마치면 양자 회로의 큐빗이 결합 구조도 상에서 어느 큐빗에 대응되는지 결정되며 비유향화된 결합 구조도 상에서 제어 큐빗과 목표 큐빗 간 최단 경로를 구할 수 있다. 제어된 게이트의 연결 변환 수는 최단 경로 상의 아크의 수이며 반전 변환은 유향화된 실제 결합 구조도의 변과 반대 방향인 아크의 수이다.
4. 수리모델
4.1 결정변수 및 계수
- bd : d번째 제어된 게이트에서 연결 변환의 횟수를 나타내는 정수형 변수
- : d번째 제어된 게이트에서 결합 구조도의 큐빗 i와 큐빗 j간 반전 변환이 발생하면 1, 아니면 0인 이진 변수
- : d번째 제어된 게이트에서 결합 구조도의 큐빗 i와 양자 회로의 큐빗 k가 서로 대응하면 1, 아니면 0인 이진 변수
- : d번째 제어된 게이트가 결합 구조도 상의 경로가 큐빗 i에서 큐빗 j로 가는 아크를 포함하면 1, 아니면 0인 이진 변수
- : d번째 제어된 게이트와 (d+1)번째 제어된 게이트 사이에서 s번의 교환 변환을 거친 후 결합 구조도의 큐빗 i에 양자 회로의 큐빗 k이 대응되면 1, 아니면 0인 이진 변수
- : d번째 제어된 게이트와 (d+1)번째 제어된 게이트 사이에서 s번째 교환 변환이 결합 구조도의 큐빗 i와 큐빗 j에서 일어났으면 1, 아니면 0인 이진 변수(단, i < j)
- cij : 결합 구조도 상에 변 (i, j)가 있으면 1, 아니면 0인 상수
- P : 결합 구조도의 큐빗의 인덱스 집합(P = {1, ⋯, |P |})
- C : 양자 회로 상 큐빗의 인덱스 집합(C = {1, ⋯, |C |})
- OB , OR , OS : 연결 변환, 반전 변환, 교환 변환의 양자 비용
- D : 제어된 게이트의 인덱스 집합(D = {1, ⋯, |D |})
- S : 제어된 게이트 간 교환 변환의 인덱스 집합 (S = {1, ⋯, |S |})
- cd, td : d번째 제어된 게이트의 제어 큐빗과 목표 큐빗
4.2 식
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
세 개 변환을 모두 사용하는 회로 변환의 경우 Siraichi et al.(2018)과 동일한 양자 비용인 OB=10, OR=4, OS=7로 설정하고, 교환 변환만을 사용하는 경우 양자 비용을 각각 OB=OR=1,000,000, OS=7로 설정한다. 목적식은 양자 비용의 총합의 최소화를 의미한다. 식 (1), 식 (2)는 양자 회로의 큐빗은 반드시 결합 구조도의 큐빗에 대응되어야 함을 의미한다. 식 (3), 식 (4)는 제어된 게이트 간 교환 변환을 거친 후에도 이러한 대응 조건은 유지되어야 함을 의미한다.
식 (5)~식 (13)은 교환 변환에 대한 제약식이다. 식 (5)는 교환 변환이 동시에 일어날 수 없음을 의미하고 식 (6)은 교환 변환의 발생 순서와 실제 변수의 순서 인덱스가 동일함을 의미한다. 식 (7), 식 (8)은 제어된 게이트 간 교환 변환 전과 교환 변환 후 결합 구조도의 큐빗들과 양자 회로의 큐빗들 간 대응 관계가 각각 이전 제어된 게이트와 이후 제어된 게이트의 큐빗들 간 대응 관계와 동일함을 의미한다. 식 (9), 식 (10)은 교환 변환이 발생하지 않으면 결합 구조도와 회로의 큐빗들 간 대응 관계가 달라지지 않음을 의미하며 식 (11)은 결합 구조도 상에서 교환 변환이 발생한 큐빗들은 결합 구조도와 회로의 큐빗들 간 대응 관계가 달라짐을 의미한다. 식 (12)는 교환 변환이 결합 구조도의 아크의 양 끝점에서만 일어날 수 있음을 의미하며, 식 (13)은 교환 변환이 양자 회로의 큐빗이 결합 구조도의 큐빗에 대응된 경우에 일어날 수 있음을 의미하는 식이다. 식 (14)~식 (19)는 결합 구조도 상의 최소 유량 문제의 제약식이다. 식 (20), 식 (21)은 각각 연결 변환, 반전 변환의 수에 관한 식이다.
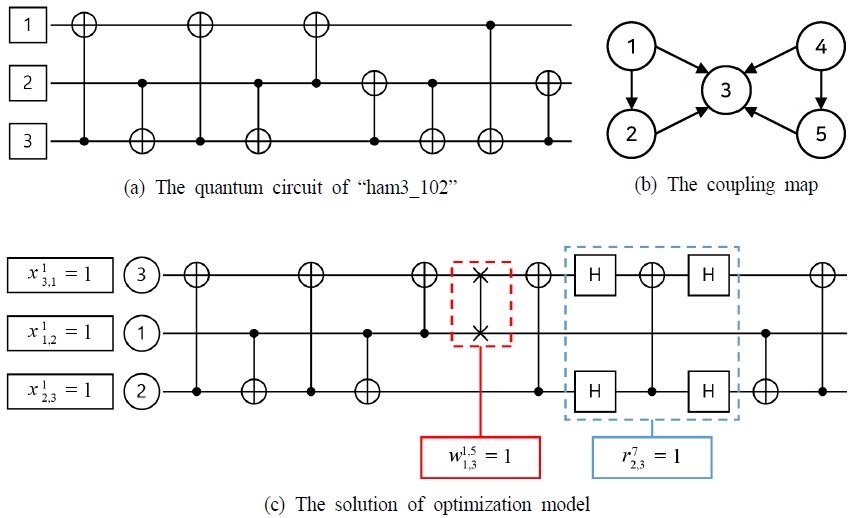
<Figure 7>은 양자 회로 ’ham3_102’에 대한 큐빗 할당 문제의 예시이다. 해에 따르면 1번째 제어된 게이트에서 결합 구조도의 큐빗 1, 2, 3은 양자 회로의 큐빗 3, 1, 2에 대응된다. 5번째 제어된 게이트와 6번째 제어된 게이트 사이에서 결합 구조도의 큐빗 1과 큐빗 2 사이에서 교환 변환이 발생하며 7번째 제어된 게이트에서 결합 구조도의 큐빗 2와 큐빗 3 사이에서 반전 변환이 발생한다. 따라서 1번의 교환 변환과 1번의 반전 변환이 발생하며 총 11의 양자 비용이 발생한다.
5. 실험결과
모델의 성능을 검증하기 위해 IBM®에서 제공하는 양자 회로와 Revlib의 양자 회로들에 대해 실험을 진행했다. 실험 환경은 Intel® Core™ i7-7700 CPU @ 3.60GHz였다. IBMQX2의 결합 구조도에 대한 큐빗 할당 문제의 양자 비용을 구하는 것을 목적으로 하며, Revlib에서 제공하는 회로 중 2개 이상의 제어 큐빗을 가지는 제어된 게이트를 포함하는 회로의 경우 단일 큐빗 게이트와 CNOT 게이트들로 분해했다. 또한, 해의 성능을 검증하기 위해 Siraichi et al.(2018)와 Wille et al.(2014)의 휴리스틱의 해와 비교했다. Siraichi et al.(2018)의 휴리스틱은 python을 통해 구현했다. Wille et al.(2014)의 휴리스틱의 결과값은 그 논문의 결과 데이터를 인용했다.
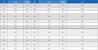
그 결과는 <Table 1>과 같았다. <Table 1>의 첫 번째 행은 양자 회로에 대한 정보에 대한 행으로 회로의 큐빗 수와 제어된 게이트의 수를 명시한다. 다음 행은 3개 변환을 모두 사용하는 모형을 통해 구한 양자 비용과 Siraichi et al.(2018)의 휴리스틱을 통해 구한 양자 비용과 비교한다. 마지막 행은 교환 변환만을 사용하는 회로 변환에 대해, 이 연구에서 제시하는 모형을 통해 구한 양자 비용과 Wille et al.(2014)의 실험 결과와 비교했다. 각 행은 이 연구에서 제시하는 모형의 계산 시간과 양자 비용, 기존 휴리스틱에 의한 양자 비용, 휴리스틱에 의한 양자 비용에 대한 본 모형에 의한 양자 비용의 비율로 구성된다. 이 중 양자 비용의 비율을 나타내는 항목인 비율(ratio) 행의 경우 본 모형이 휴리스틱에 의한 양자 비용을 어느 만큼 감소시키는지 정성적으로 보여주는 지표이다. 본 모형은 Siraichi et al.(2018)의 휴리스틱에 의한 양자 비용을 평균 58%까지 감소시킬 수 있으며, 최대 34%까지 감소시키는 것이 가능했다. 또한, 본 모형을 통한 실험 결과는 항상 휴리스틱의 결과의 양자 비용보다 더 적은 양자 비용을 가지는 큐빗들 간 대응 관계와 양자 회로 변환을 제시한다. 모형을 통해 얻은 결과값은 추후 연구되는 큐빗 할당 문제 해결 휴리스틱의 성능 검증을 위한 정성적 척도로 활용 가능하다.
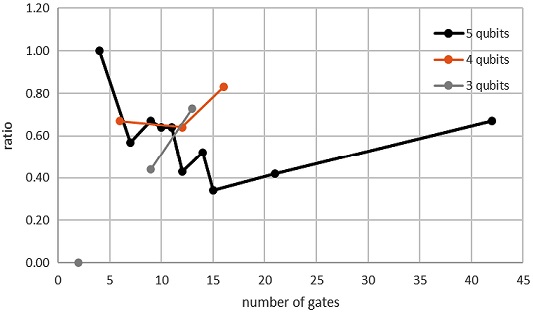
제어된 게이트 수와 양자 비용의 감소 비율의 관계를 확인하기 위해 같은 수의 큐빗을 가지는 양자 회로들에 대해 양자 회로의 비율을 비교했다. 이를 분산형 그래프로 표현하면 <Figure 8>과 같다. <Figure 8>의 가로축은 양자 회로의 제어된 게이트 수를 나타낸다. 세로축은 Siraichi et al.(2018)의 휴리스틱에 대한 비율을 나타낸다. 3개나 4개 큐빗을 가지는 양자 회로의 경우 큐빗과 제어된 게이트 수가 적고 각 집합에 포함되는 양자 회로의 수가 적어 유의미한 결과를 얻기 힘들다. 따라서 5개 큐빗을 가지는 10개의 양자 회로에 대해 분석한 결과 15개 이하의 제어된 게이트들을 가지는 회로들의 경우 대체적으로 양자 회로의 제어된 게이트 수가 증가할수록 비율은 감소함을 확인할 수 있다. 다만 21개와 42개의 큐빗을 가지는 양자 회로인 “alu-v0_26”과 “pea”의 경우 15개 큐빗을 가지는 “4gt13_92”와 비교했을 때 비율이 증가한다. 따라서 제어된 게이트 수가 증가할수록 비율이 감소하는 경향을 더 많은 양자회로에 대한 실험을 통해 검증할 필요성이 있다. 다만 Revlib에서 제공하는 양자 회로가 너무 많은 수의 제어 큐빗을 가지는 경우 단일 큐빗 게이트와 CNOT 게이트로 분해할 수 없어 실험을 진행할 수 있는 양자 회로의 수가 적었다. 또한, Wille et al.(2014) 휴리스틱의 결과값은 논문의 결과 데이터 중 모델에서 실험을 돌린 회로에 대한 결과 데이터만 인용했기에 모델과 휴리스틱의 결과값을 비교할 수 있는 회로의 수가 적었다. 따라서 모델에 대한 성능을 검증하기 위해 실험 가능한 양자 회로를 추가로 확보해야 한다.
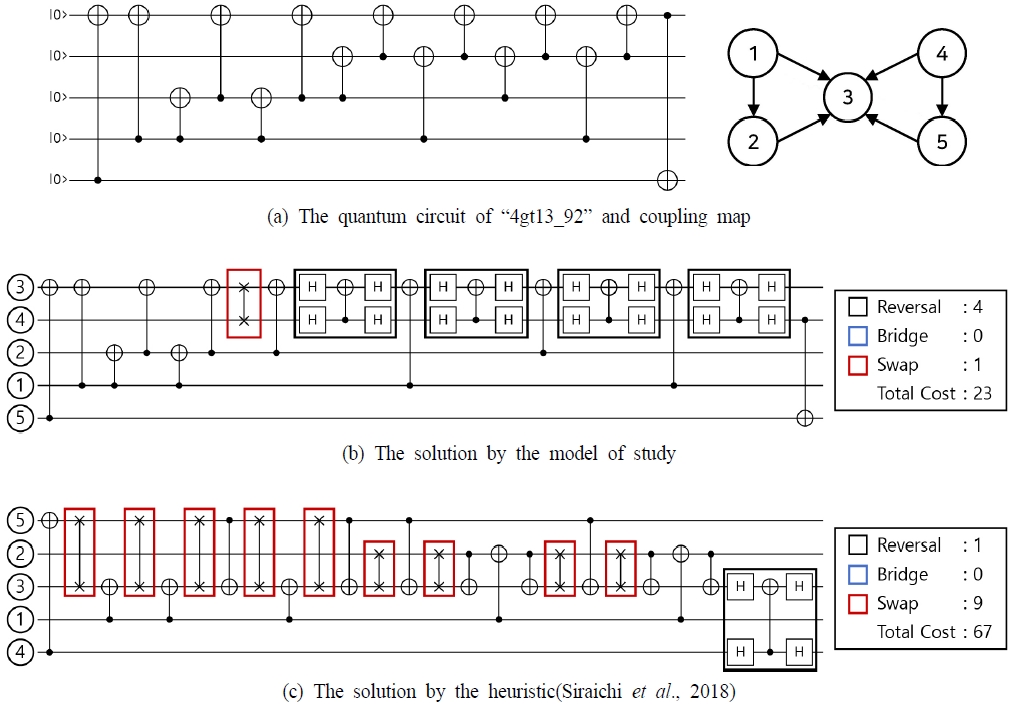
한편, <Figure 9>는 양자 회로 ‘4gt13_92’의 양자 회로에 대한 회로 변환 결과로 모델에 의한 변환은 휴리스틱에 의한 변환들보다 적은 변환을 이용했다. 또한, 상대적으로 높은 양자 비용을 가지는 교환 변환의 수를 비교했을 때 모델에 의한 변환이 그 수가 더 적었다.
6. 결 론
큐빗 할당 문제는 양자 회로를 실제 양자컴퓨터에서 구현할 때 양자 회로의 정확도를 높이고 양자 오차의 정성적인 기준인 양자 비용을 줄이기 위해 최적해를 찾아야 하는 문제이다. 이 연구의 정수계획 모형을 통해 최소의 양자 비용을 가지는 큐빗 할당 관계와 양자 회로 변환을 구할 수 있다. 이 연구는 휴리스틱 방법론을 활용한 기존 연구들과 달리 정수계획 모델의 해를 구하여 최소의 양자 비용을 가지는 큐빗들 간 대응 관계와 회로 변환을 제시하였다. 실제로 이 연구의 정수계획 모델의 실효성을 검증하기 위해 기존의 휴리스틱 방법론의 해를 비교한 결과 최대 33%까지 양자 비용을 줄이는 것이 가능하다. 또한, 이 연구에서 제시하는 수리 계획 모형은 기존 휴리스틱의 성능을 평가하는 데 사용될 수 있다.
이 연구에서 제시하는 정수계획 모형은 최적 큐빗 할당 방식을 제공한다. 하지만, 실제 양자컴퓨터의 큐빗 수나 양자 회로의 큐빗 수, 회로의 제어된 게이트 수가 증가할수록 모형의 크기가 지수적으로 증가하는 문제점이 있다. 또한, 이 연구에서 제시한 실험 결과의 대상이 되는 양자 회로들은 매우 적은 수의 큐빗을 가진다. 실제로, 더 많은 수의 큐빗을 가지는 양자 컴퓨터에 현실 적용을 위해서는 제시된 수리 모형을 활용한, 모형기반 휴리스틱 방법론 개발 연구가 필요하다. 더불어, 이 연구에서 고려하지 않은 양자컴퓨터의 큐빗 별 관측 에러를 포함한 최적의 큐빗 할당 방법에 대해 추가 연구가 필요하다.
Acknowledgments
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2017R1E1A1A03070988, No.2020R1A4A3079864).
References
-
Ajagekar, A., Humble, T., and You, F. (2020), Quantum Computing based Hybrid Solution Strategies for Large-Scale Discrete-Continuous Optimization Problems, Computers and Chemical Engineering, 132, 106630.
[https://doi.org/10.1016/j.compchemeng.2019.106630]

-
Alfailakawi, M., Ahmad, I., and Hamdan, S. (2016), Harmony-Search Algorithm for 2D Nearest Neighbor Quantum Circuits Realization, Expert Systems with Applications, 61, 16-27.
[https://doi.org/10.1016/j.eswa.2016.04.038]

-
Balensiefer, S., Kregor-Stickles, L., and Oskin, M. (2005), An Evaluation Framework and Instruction Set Architecture for Ion-Trap based Quantum Micro-Architectures, In 32nd International Symposium on Computer Architecture (ISCA’05), IEEE, 186-196.
[https://doi.org/10.1145/1080695.1069986]

-
Barenco, A., Bennett, C., Cleve, R., DiVincenzo, D., Margolus, N., Shor, P., Sleator, T., Smolin, J., Weinfurter, H. (1995), Elementary Gates for Quantum Computation, Physical Review A, 52(5), 3457-3467.
[https://doi.org/10.1103/PhysRevA.52.3457]

-
Castelvecchi, D. (2017), IBM’s Quantum Cloud Computer Goes Commercial, Nature News, 543(7644), 159.
[https://doi.org/10.1038/nature.2017.21585]

-
Ding, J. and Yamashita, S. (2020), Exact Synthesis of Nearest Neighbor Compliant Quantum Circuits in 2-D Architecture and Its Application to Large-Scale Circuits, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 39(5), 1045-1058.
[https://doi.org/10.1109/TCAD.2019.2907919]

-
Farghadan, A. and Mohammadzadeh, N. (2017). Quantum Circuit Physical Design flow for 2D Nearest-Neighbor Architectures, International Journal of Circuit Theory and Applications, 45(7), 989-1000.
[https://doi.org/10.1002/cta.2335]

-
Farghadan, A. and Mohammadzadeh, N. (2019), Mapping Quantum Circuits on 3D Nearest-Neighbor Architectures, Quantum Science and Technology, 4(3), 035001.
[https://doi.org/10.1088/2058-9565/ab177a]

-
King et al. (2019), Quantum Annealing Amid Local Ruggedness and Global Frustration, Journal of the Physical Society of Japan, 88(6), 061007.
[https://doi.org/10.7566/JPSJ.88.061007]

-
Kole, A., Datta, K., and Sengupta, I. (2016), A Heuristic for Linear Nearest Neighbor Realization of Quantum Circuits by SWAP Gate Insertion Using N-Gate Lookahead, IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 6(1), 62-72.
[https://doi.org/10.1109/JETCAS.2016.2528720]

-
Kole, A., Datta, K., and Sengupta, I. (2018), A New Heuristic for N-Dimensional Nearest Neighbor Realization of a Quantum Circuit, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 37(1), 182-192.
[https://doi.org/10.1109/TCAD.2017.2693284]

-
Lye, A., Wille, R., and Drechsler, R. (2015), Determining the Minimal Number of SWAP Gates for Multi-Dimensional Nearest Neighbor Quantum Circuits, The 20th Asia and South Pacific Design Automation Conference.
[https://doi.org/10.1109/ASPDAC.2015.7059001]

-
Montanaro, A. (2016), Quantum Algorithms : An Overview, npj Quantum Information, 2(1), 1-8.
[https://doi.org/10.1038/npjqi.2015.23]

- Murgia, M. and Waters, R. (2019), Google Claims to have Reached Quantum Supremacy, Financial Times, 20.
-
Ruffinelli, D. and Barán, B. (2017), Linear Nearest Neighbor Optimization in Quantum Circuits : A Multiobjective Perspective, Quantum Information Processing, 16(9), 220.
[https://doi.org/10.1007/s11128-017-1662-3]

-
Shafaei, A., Saeedi, M., and Pedram, M. (2014), Qubit Placement to Minimize Communication Overhead in 2D Quantum Architectures, 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC).
[https://doi.org/10.1109/ASPDAC.2014.6742940]

-
Shrivastwa, R., Datta, K., Sengupta, I. (2015), Fast Qubit Placement in 2D Architecture Using Nearest Neighbor Realization, 2015 IEEE International Symposium on Nanoelectronic and Information Systems.
[https://doi.org/10.1109/iNIS.2015.59]

-
Siraichi, M. Y., Santos, V. F. D., Collange, S., and Pereira, F. M. Q. (2018), Qubit Allocation, In Proceed ings of the 2018 International Symposium on Code Generation and Optimization, 113-125.
[https://doi.org/10.1145/3168822]

-
Wille, R., Lye, A., and Drechsler, R. (2014), Exact Reordering of Circuit Lines for Nearest Neighbor Quantum Architectures, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 33(12), 1818-1831.
[https://doi.org/10.1109/TCAD.2014.2356463]

-
Wille, R., Lye, A., and Drechsler, R. (2014), Optimal SWAP Gate Insertion for Nearest Neighbor Quantum Circuits, 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC).
[https://doi.org/10.1109/ASPDAC.2014.6742939]

-
Zulehner, A., Paler, A., and Wille, R. (2018), Efficient Mapping of Quantum Circuits to the IBM QX Architectures, 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE).
[https://doi.org/10.23919/DATE.2018.8342181]

-
Zulehner, A., Paler, A., and Wille, R. (2019), An Efficient Methodology for Mapping Quantum Circuits to the IBM QX Architectures, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 38(7), 1226-1236.
[https://doi.org/10.1109/TCAD.2018.2846658]

최현석 : 고려대학교 산업경영공학부에서 2018년 학사학위를 취득하고 고려대학교에서 산업경영공학과 박사과정에 재학 중이다. 연구분야는 최적화이다.
최인찬 : 고려대학교에서 1982년 산업공학 학사학위를 취득하고, Iowa State University 1984년 산업공학 학사학위를 취득하였다. 1986년 Columbia University에서 경영과학(수리계획) 석사, 1990년 경영과학(수리계획) 박사학위를 취득하였다. 벨통신연구소(Bellcore) Tech Research Staff, 위치타 주립대학교 조교수, 매사추세츠 공과대학교 객원교수를 역임하고 1996년부터 고려대학교 산업경영공학과 교수로 재직하고 있다. 관심 연구분야는 수리계획법, 최적화, 양자컴퓨팅이다.