다중 식별자를 이용한 Adversarial Autoencoder 기반 제조 공정 이상 탐지

1. 서 론

최근 제조 공정은 점점 더 미세화가 되어가고 있고 이로 인해 높은 생산성을 달성하며 더 많은 수익을 창출할 수 있게 되었다. 또한, 스마트팩토리(smart factory)가 구축되어 엔지니어에 의존하지 않고 자동적인 생산 시스템을 구축할 수 있게 되었다. 자동화가 이루어진 생산 시스템에서는 여러 종류의 센서 데이터들이 실시간으로 생성된다. 공정이 진행되는 동안 실시간으로 생성되는 데이터의 종류는 정상 데이터와 이상 원인에 의한 이상 데이터이다.

공정의 미세화와 자동화가 이루어질수록 공정은 고도화된 시스템들로 구성됨으로써 그에 맞는 고도화된 이상 탐지가 필요하다. 공정 이상은 수율(yield)을 저하시키는 원인이며 품질 불량을 유발한다. 이는 공장 전체에 파급 효과가 있어 생산에 매우 치명적이다. 이상이 발생되면 제조 공정이 중단되고 매우 큰 손실이 일어나게 된다. 이상을 바로 탐지하지 못할 경우, 그 피해는 더 커지므로 빠른 감지가 절실하다.

하지만, 센서의 이상 유무는 전문가들의 경험으로 알아내는 것이 대부분이기 때문에 이상 탐지가 쉽지 않다. 더욱이 시스템의 복잡도가 높아짐에 따라 관리가 어려워지므로, 정확하게 이상을 탐지하고 이상 원인을 분류하는 것이 중요하다. 이상 데이터는 정상 데이터보다 빈도가 낮게 발생한다. 이를 이용하여 지도학습으로 분류 모형을 학습하게 된다면 분류 성능이 떨어지는 원인이 된다. 따라서, 본 논문에서는 정상 데이터로만 분류 모델을 학습하는 비지도학습으로 정상과 이상을 분류할 수 있는 모델을 구축한다. 학습된 모델을 통해 정상 데이터와 다른 특성을 따르면 이상 데이터로 판정한다.

기존에 연구된 이상 탐지 방법은 여러 가지가 있다. 그중 하나인 Autoencoder(AE)는 학습 단계에서 입력 값을 똑같이 복원해 내는 목적 함수를 갖고 있다. 이는 비지도학습 방식으로 입력 데이터의 노이즈(noise)를 제거하며 모델을 학습시킴으로써 차원 축소를 위한 입력 데이터의 특징을 배우는 알고리즘이다. 학습이 완료된 AE를 활용한 이상치 탐지는 MSE(Mean Squared Error) 손실 함수를 사용한다. 입력과 복원의 차이(reconstruction error)를 일정 임계값(threshold)의 비교를 통해 이상 여부를 결정한다. 만약 이상 데이터가 정상 데이터로 학습된 AE를 통과할 경우, 복원 오차는 커질 것이므로 이상 데이터로 판별할 수 있다. 하지만, MSE 손실 함수는 확실하지 않은 부분을 평균값으로 예측하기 때문에 복원 결과를 흐리게(blur) 나오게 하는 경우가 있다. 복원 성능 하락은 이상치 탐지 성능에 영향을 끼칠 수 있다(Kim et al., 2020).

AAE(Adversarial Autoencoder)는 AE 구조에 잠재 분포(latent distribution)를 검사하는 식별자를 도입하는 구조로 AE보다 좀 더 효율적으로 이상 탐지를 할 수 있다. AE와 마찬가지로 정상 데이터만으로 학습할 수 있고 학습된 모델을 통해 정상 데이터와 이상 데이터를 분류하고 탐지한다. 또한, Variational Autoencoder(VAE)와는 다르게 실제 데이터의 분포를 정규분포로 전제하지 않아도 된다는 장점을 갖고 있다. AAE 기반 이상 탐지는 AE 기반 이상 탐지와 유사한 과정으로 복원 오차와 임곗값의 비교를 통해 이상 데이터를 판별한다(Makhzani et al., 2015).

본 논문은 제조 공정의 이상 탐지를 위한 AE 기반의 새로운 방법론을 제시한다. 이상 데이터는 정상 데이터에 비해 빈도가 훨씬 작아 클래스 불균형이 크므로, 정상 데이터만을 활용하여 비지도학습으로 AE를 학습한다. 학습 후, 입력 데이터와 복원 데이터의 차이가 큰 경우에 이상 데이터로 판정하도록 하였다. 이때, 학습 데이터인 정상 데이터에 대한 복원력을 높이기 위해 AE에 3개의 식별자를 도입하여 경쟁 학습을 하도록 하였다.

이는 모델의 입력 데이터가 이상 유무를 알 수 없는 데이터 일 때, 정상 데이터의 특징과 다른 경우 이상 데이터로 판별함으로써 이상 탐지를 효과적으로 할 수 있는 방법을 제공하고자 한다.

본 논문의 구성은 다음과 같다. 제 2장에서는 본 논문에서 제안하는 방법에 관해서 설명한다. 제 3장은 제안 방안의 성능을 검증하고, 마지막으로 제 4장은 결론에 관해 기술한다.

2. 이상치 탐지 모델

이상치는 정상적인 패턴을 따르지 않는 데이터(Chandola et al., 2009), 진정한 확률 밀도(true probability density)가 낮은 데이터(Harmeling et al., 2006)라고 정의할 수 있다. 이처럼 이상치에 대한 정의는 다양하다.

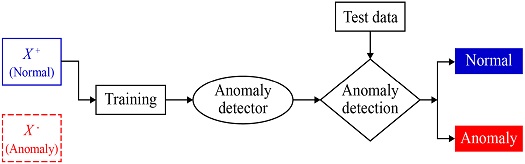
이상 탐지 알고리즘은 <Figure 1>과 같이 데이터의 이상 여부를 판별하는 과정으로 이루어진다. 신용카드 사기 여부, 자율 자동차 주행, 비디오 감시, 제조 공정에서의 이상 검출 등과 같은 다양한 분야에서 사용된다. 본 연구는 시계열 데이터에 대한 이상 탐지이다. 시계열 데이터 이상 탐지 문제는 주어진 기간의 신호가 정상 패턴에서 벗어나면 이상치로 판정하여 탐지하는 것이다.

Figure 1.

Anomaly Detection Method

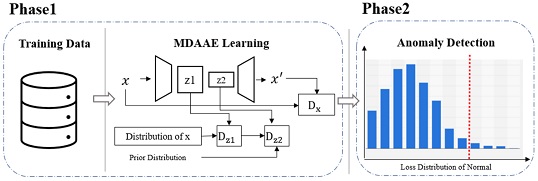
제조 공정에서 이상치를 탐지하기 위해서 <Figure 2>와 같이 2단계로 구성된 모델을 제안한다. 1단계는 Adversarial Autoencoder with Multiple Discriminators (MDAAE)를 통해서 정상 클래스 데이터를 학습하는 과정이며 2단계에서는 학습을 완료한 MDAAE를 통해 입력 데이터와 복원 데이터의 차이를 임계점을 기준으로 이상치 여부를 판정하는 과정이다.

Figure 2.

The Proposed Method

2.1 MDAAE를 활용한 학습

제조 공정에서 수집할 수 있는 데이터는 대부분 정상 데이터이다. 이상 데이터는 매우 희귀하므로 종류를 알 수 없기 때문에 정상 데이터만을 사용하여 이상치 여부를 판정할 수 있는 모델이 필요하다. 제안 방법은 AAE 기반 모델이므로, 정상 데이터 값 자체보다는 타겟 분포인 정상 데이터의 분포를 학습한다(Makhzani et al., 2015).

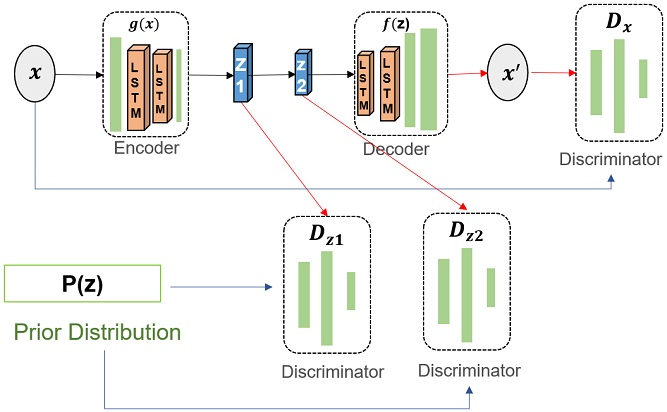
본 논문에서 제안하는 모델은 <Figure 3>과 같이 AE의 구조(인코더와 디코더)와 3개의 식별자인 D_z1, D_z2, D_x로 구성되어 있다.

Figure 3.

The Structure of MDAAE

정상 데이터인 입력 데이터가 ‘인코더’ 모델에 들어가게 되면 고차원의 데이터가 저차원의 데이터로 변하게 된다. 사용자가 지정한 차원인 ‘잠재 공간(latent space) z1’에 매핑(mapping) 된다. 인코더를 통과시키는 과정은 고차원에서 저차원으로의 매핑 과정일 뿐만 아니라 노이즈를 제거하는 작업이다. 잠재 공간 z1는 입력 데이터를 잘 설명할 수 있는 특질을 추출한다. 이는 정보량이 높은 특질들이 우선적으로 추출된다. 잠재 공간 z1에서 다시 한번 입력 데이터를 잘 설명할 수 있는 특질인 더 작은 차원의 잠재 공간 z2를 추출한다. 잠재 공간 z2에서 추출된 특질들이 ‘디코더’에 통과되면 특질들을 기반으로 입력 데이터와 같은 차원의 데이터로 복원된다.

이때, 식별자 D_z1, D_z2를 통해서 입력 데이터의 사전분포(prior distribution)와 잠재 공간 z1, 그리고 잠재 공간 z2가 비슷해지도록 경쟁 학습을 시킨다. 경쟁 학습이란 GAN(Generative Adversarial Network)의 모델에서 사용되는 용어이다. GAN은 생성자와 식별자를 경쟁적으로 학습을 시키는데 생성자는 가짜 데이터를 만들어서 식별자를 속이는 목적을 가지고 있고, 식별자는 생성자가 만든 가짜 데이터와 진짜 데이터를 구분하는 목적을 가지고 있다. 이 둘을 함께 학습시키면서 진짜 같은 가짜 데이터를 만들 수 있는 생성자를 얻을 수 있게 된다. 이것이 경쟁 학습이다(Goodfellow et al., 2014).

AAE와 마찬가지로 사전분포가 가우시안 분포를 따른다고 가정하지 않고도 원하는 형태의 잠재 분포를 강제시킬 수 있다는 점을 이용하였다.

D_x를 통해서 입력 데이터와 복원된 데이터를 비슷하게 만들어 최대한 입력 데이터의 특질들을 복원시킬 수 있도록 해준다.

인코더와 디코더의 구조로는 시간 흐름에 따라 구성되는 시계열 데이터의 상관 특성을 학습하는데 적합한 LSTM(Long Short-Term Memory)을 사용한다. LSTM은 뉴럴 네트워크(neural network)에서 히든 레이어(hidden layer)가 연결되어 순환 구조를 이루는 신경망의 한 종류인 Recurrent Neural Network(RNN)의 학습에서 기울기 손실(gradient vanishing) 문제를 완화해 줄 방안으로 고안된 알고리즘이다. LSTM은 RNN에 비해 과거의 정보를 반영할 수 있는 장점이 있다. LSTM은 지나온 시점의 변화 패턴을 학습할 수 있으므로 시계열 데이터를 학습하는데 높은 성능을 발휘한다. 이때, 이전 데이터의 관계뿐만 아니라 이후 데이터의 관계도 학습할 수 있는 양방향(bidirection) LSTM을 사용한다(Hochreiter et al., 1997).

모델 학습에 필요한 손실 함수는 4가지이다. 3가지의 적대적 손실(adversarial loss)과 1가지의 복원 오차(reconstruction error)로 구성된다.

식별자 D_z1의 손실 함수는 식 (1)과 같은 목적식을 가지고 있다. 인코더 g는 입력 데이터 x를 사전분포와 비슷한 잠재 공간 z1과 같아지도록 학습한다. 식별자 D_z1는 인코더 g에 의해 생성되는 데이터와 사전분포를 완벽하게 구별하려고 한다. 인코더 g는 식 (1)을 최소화하려고 하고 식별자 D_z1는 식 (1)을 최대화하려고 한다.

$\[ \begin{array}{c}Max{L}_{adv-d_{z1}\left(x,g,D_{z1}\right)}\hfill \\ =E\left[\log \left(D_{z1}\left(p\left(z1\right)\right)\right)+E\left(\log \left(1-D_{z1}\left(g\left(x\right.\right)\right)\right)\right]\hfill \end{array} \]$

(1)

Discriminator D_z2의 손실 함수는 식 (2)와 같이 정의될 수 있다. 인코더 g는 입력 데이터 x를 사전분포와 비슷한 잠재 공간 z2과 같아지도록 학습한다. 식별자 D_z1는 인코더 g에 의해 생성되는 데이터와 사전분포를 완벽하게 구별하려고 한다. 인코더 g는 식 (2)를 최소화하려고 하고 식별자 D_z2는 식 (2)를 최대화하려고 한다.

$\[ \begin{array}{c}Max{L}_{adv-d_{z2}\left(x,g,D_{z2}\right)}\hfill \\ =E\left[\log \left(D_{z2}\left(p\left(z2\right)\right)\right)+E\left(\log \left(1-D_{z2}\left(g\left(x\right.\right)\right)\right)\right]\hfill \end{array} \]$

(2)

식별자 D_x의 손실 함수는 식 (3)과 같이 정의될 수 있다. 디코더 f는 사전분포로부터 복원 데이터 x를 생성하려고 한다. 식별자 D_x는 디코더 f에 의해 생성된 데이터와 입력 데이터 x를 완벽하게 구별하려고 한다. 디코더 f는 식 (3)을 최소화하려고 하고 식별자 D_x는 식 (3)을 최대화하려고 한다.

$\[ \begin{array}{c}Max{L}_{adv-d_x\left(x,g,D_x\right)}\hfill \\ =E\left[\log \left(D_x\left(x\right)\right)+E\left(\log \left(1-D_x\left(f\left(p\left(z\right.\right.\right)\right)\right)\right]\hfill \end{array} \]$

(3)

AE 손실 함수인 식 (4)는 입력 데이터와 복원 데이터의 차이를 최소화하는 목적을 갖고 있다.

$\[ L_{error}\left(x,g,f\right)=E_z\left[\log \left(p\left(f\left(g\left(x\right)\right)\left|x\right.\right)\right)\right] \]$

(4)

전체 손실 함수는 식 (5)과 같다.

$\[ \begin{array}{c}L\left(x,g{D}_{z1},D_{z2},D_{x,f}\right)\hfill \\ =L_{adv-d_x}\left(x,D_{x,f}\right)+L_{error}\left(x,g,f\right)\hfill \\ +L_{adv-d_{z1}}\left(x,g,D_{z1}\right)+L_{adv-d_{z2}}\left(x,g,D_{z2}\right)\hfill \end{array} \]$

(5)

3. 실 험

본 연구에서 제안하는 이상 탐지 방법론의 성능을 평가하기 위해 제조 공정에서 발생하는 데이터를 대상으로 실험을 수행하였다. 데이터는 총 네 가지를 사용하였다. NASA 베이링 데이터 셋은 클래스 정보가 없기 때문에 분류 성능 평가를 할 수 없어서 복원력 측정을 하였다. 그 외 세 개의 데이터에는 클래스 정보가 있어서 이상 탐지 분류 성능을 측정하였다.

3.1 데이터 셋

(1) NASA 베어링 데이터 셋

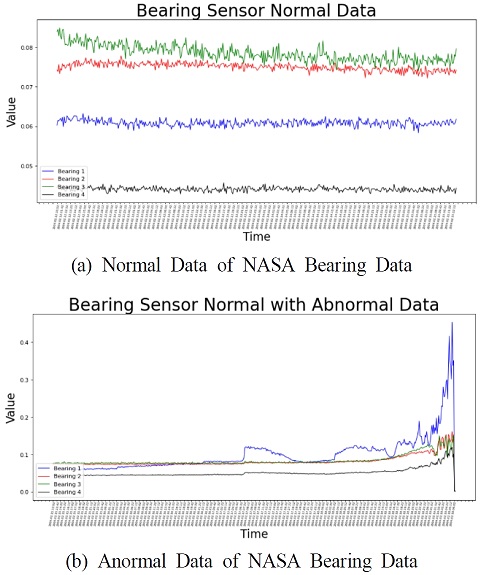
실험에서 사용한 데이터 중 첫 번째 데이터는 NASA 베어링 데이터 셋이다. NASA 연구에서 수집된 센서 판독 값은 일정 기간 동안 부하 상태에서 고장 난 4개의 베어링에 대해 측정되었다. 이 데이터 셋은 10분 간격으로 기록된 1초 진동 신호 개별 파일로 구성된다. 각 파일에는 한 베어링 당 20,480개의 센서 값을 가지고 있다. 베어링의 기계적 열화는 시간이 지남에 따라 점차 발생한다고 가정된 데이터이다. 전체 데이터 셋에 대해 푸리에 변환(fourier transform)을 사용하여 신호를 시간 영역에서 주파수 영역으로 변환하여 변화를 확인해 보았다. 베어링 고장으로 이어지는 시스템의 주파수 진폭이 증가하는 것을 알 수 있었다. 이를 이상 구간이라고 가정을 하고 실험을 진행하였다.

전체 데이터의 앞부분인 정상적인 작동에서 측정된 데이터를 모델 학습에 사용하였고 이는 전체 9,216개로 데이터 셋의 45%이다. 정상 데이터와 이상 데이터가 섞인 데이터의 뒷부분을 복원력 테스트에 사용하였다. 이는 11,264개로 전체 데이터 셋의 55%이다. 복원력 테스트를 통하여 모델의 성능을 평가하였다. <Figure 4>의 (a)는 주파수 영역의 정상적인 작동을 나타내며 <Figure 3>의 (b)는 주파수 영역의 베어링 오류로 이어지는 센서 판독 값이 포함된 데이터 셋의 작동을 나타낸다.

Figure 4.

Description of NASA Bearing Data

(2) 웨이퍼 제어 특정 데이터 셋

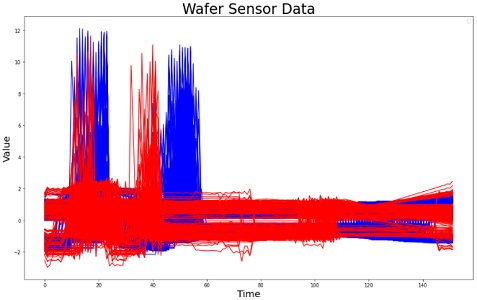
두 번째 데이터 셋은 제조용 실리콘 웨이퍼 처리 중 다양한 센서에서 기록된 인라인 프로세스 제어 측정값을 수집하여 구성된 웨이퍼 데이터베이스이다. 웨이퍼 데이터베이스의 각 데이터 셋에는 한 개의 웨이퍼를 하나의 장비로 가공하는 동안 한 센서에서 기록한 측정치가 포함되어 있다. 클래스는 정상과 이상이다. 데이터는 총 7,164개이며 각 데이터의 길이는 152이다.

<Figure 5>는 파란색으로 나타낸 정상 데이터와 빨간색으로 나타낸 이상 데이터를 보여준다. 정상 클래스 데이터는 6,402개로 89.36%를 차지하고, 이상 클래스의 데이터는 762개로 10.64%를 차지한다. 이 데이터 셋은 클래스 불균형이 큰 것을 알 수 있다.

Figure 5.

Description of Wafer Dataset

학습 데이터로는 클래스 불균형 문제를 해결하기 위해 정상 데이터로만 구성을 하였고 5,499개를 사용하였다. 테스트로는 1,665개의 데이터를 사용하였고 정상 903개 이상 762개로 구성하였다.

(3) FordA 데이터 셋

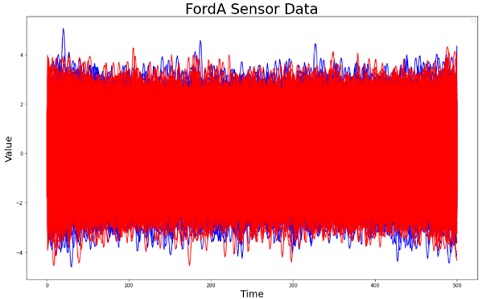
FordA 데이터 셋은 1년에 걸쳐 수집한 자율주행차 데이터로 구성되어 있다. 특정 이상 증상의 존재 여부에 따라 클래스가 할당되었다. 클래스는 정상과 이상이다. 데이터는 총 4,921개이며 각 데이터의 길이는 501이다.

<Figure 6>은 파란색으로 나타낸 정상 데이터와 빨간색으로 나타낸 이상 데이터를 보여준다. 정상 클래스 데이터는 3,601개로 73.18%를 차지하고, 이상 클래스의 데이터는 1,320개로 26.82%를 차지한다. 이 데이터 셋은 클래스 불균형이 큰 것을 알 수 있다.

Figure 6.

Description of FordA Dataset

학습 데이터 셋으로는 클래스 불균형 문제를 해결하기 위해 정상 데이터로만 구성을 하였고 2,281개를 사용하였다. 테스트 데이터 셋으로는 2,640개의 데이터를 사용하였고 정상 데이터 1,320개 이상 데이터 1,320개로 구성하였다. 이는 정상 데이터와 이상 데이터의 비율을 같게 하기 위함이다.

(3) FordB 데이터 셋

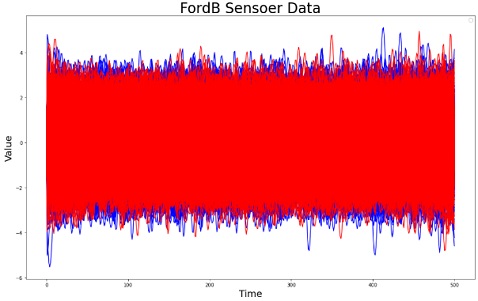
FordB 데이터 셋은 FordA 데이터 셋과 마찬가지로 1년에 걸쳐 수집한 자율주행차 데이터로 구성되어 있으며 클래스는 정상과 이상이다. 특정 이상 증상의 존재 여부에 따라 클래스가 할당되었다. 데이터는 총 4,446개이며 각 데이터의 길이는 501이다.

<Figure 7>는 파란색으로 나타낸 정상 데이터와 빨간색으로 나타낸 이상 데이터의 차이를 보여준다. 정상 클래스 데이터는 3,636개로 81.78%를 차지하고, 이상 클래스의 데이터는 810개로 18.22%를 차지한다. 이 데이터 셋은 클래스 불균형이 큰 것을 알 수 있다.

Figure 7.

Description of FordB Dataset

학습 데이터로는 클래스 불균형 문제를 해결하기 위해 정상 데이터로만 구성을 하였고 2,826개를 사용하였다. 테스트로는 1,620개의 데이터를 사용하였고 정상 810개 이상 810개로 구성하였다. FordA 데이터 셋과 마찬가지로 정상 데이터와 이상 데이터의 비율을 같게 하기 위함이다.

3.2 실험 결과

(1) 복원력 평가

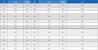
본 논문에서 제안한 모델의 복원 성능을 비교하기 위하여 AE, AAE, GPND(Generative Probabilistic Novelty Detection with Adversarial Autoencoders)를 비교 군으로 실험을 진행하였다. 동일한 조건으로 성능을 비교하기 위해서 인코더와 디코더, 식별자의 크기는 동일하게 하였다. 파라미터 설정은 <Table 1>과 같다. 디코더의 파라미터 설정은 인코더 파라미터의 역순이다.

Table 1.

Model Parameter Setup

GPND는 AAE에 식별자 한 개가 더 추가된 구조이다. 입력값을 똑같이 출력해내는 목적을 가지고 있으며 식별자를 통하여 좀 더 복원력을 높이는 효과를 가지고 있다. 이 모델의 이상 탐지 방법은 입력 값과 복원된 값의 차이가 특정 임계값을 넘으면 이상으로 판별하게 된다.

첫 번째 데이터인 NASA 베어링 데이터는 클래스 정보가 없기 때문에 복원 성능 평가 지표로 MAE (Mean Absolute Error)를 사용하였다. MAE는 MSE에 비해 이상치 영향을 적게 받는다. MSE는 오차를 제곱하기 때문에 오차가 커지면 거질 수록 손실이 제곱으로 커지게 되기 때문이다. MAE는 이상치에 강건하다는 것을 알 수 있다.

<Table 2>는 모델 별 손실 분포의 중앙값(median)이다. 이는 모델이 얼마나 입력 데이터를 비슷하게 복원시킬 수 있는지에 대한 평가로 데이터의 복원력을 나타낸다.

Table 2.

Median of Reconstruction Loss Distribution

모델 간의 복원력 차이를 비교하면 AE, AAE, GPND보다 제안하는 모델인 MDAAE의 성능이 더 우수하다는 것을 알 수 있다. 복원력이 더 좋다는 것은 모델이 정상 클래스의 특징을 좀 더 정확히 학습할 수 있다는 것과 이상치에 강건하다는 것을 알 수 있다.

(2) 이상 분류 성능 평가

웨이퍼 제어 측정 데이터 셋과 FordA, FordB 데이터 셋은 클래스 정보가 있으므로 성능 평가 방법으로 클래스 분류 정확도를 사용하였다. 마찬가지로 AE와 AAE, GPND를 비교 군으로 실험을 진행하였다. 결과는 <Table 3>과 같다.

Table 3.

Classification Accuracy

제조 생산 환경에서는 이상 데이터를 분류하는 것이 정상 데이터를 분류하는 것보다 매우 중요하다. 제조 공정에서 이상 탐지는 제조의 수율을 높이고 손실을 줄이기 위해 필수적인 작업이기 때문이다.

모델 별 손실 분포의 95%를 임계값으로 사용하여 평가를 진행하였는데 이상 데이터 분류 성능은 AE, AAE, GPND보다 제안하는 MDAAE 모델의 이상 탐지 성능이 더 우수하다는 것을 알 수 있다.

4. 결 론

본 연구는 제조 공정에서 수집되는 시계열 데이터를 활용하여 이상 탐지 방법론을 제시하였다. 공정 이상 발생은 제품 품질과 공정 성능을 저하시키게 되는 원인이다. 공정 이상으로부터 발생하게 되는 큰 손실을 방지하기 위해 공정 이상 탐지가 중요하다. 하지만, 정상 데이터에 비해 이상 데이터의 수가 현저히 적기 때문에 데이터 불균형 문제가 발생하게 된다. 빈도가 높은 정상 데이터를 비지도학습 방법인 AE의 복원력이 정상 데이터에서는 높으나 이상 데이터에 대해 현저히 떨어질 것이라는 점에 착안하여 복원력을 높이기 위한 새로운 방법을 제시하였다.

본 연구에서는 정상 데이터로만 MDAAE 학습한 후, 복원 오차와 임계값을 비교하여 이상치 여부를 판정한다. 실험을 통해서 본 연구의 제안 방법이 뛰어난 이상 분류 성능을 보임을 확인하였다. 제안된 방법론은 높은 분류 정확도를 달성하여 실용적 가치가 클 것으로 기대된다.

이는 제조 시스템뿐만 아니라 시계열 데이터가 존재하는 다양한 분야에도 적용이 가능할 것으로 기대한다. 본 연구에서 실험한 데이터는 시계열 데이터로 시간 순서를 고려해야 한다는 조건이 있다. 시계열 데이터뿐 아니라 이미지 데이터에도 적용할 수 있는 추가적인 연구가 필요하다.

Acknowledgments

제16회 석사논문경진대회 수상논문.

이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구(NRF-2019R1A2C2005949)이며, 4단계 두뇌한국21에 의해 지원되었습니다.

References

• Abou-Nasr, M. and Feldkamp, L., Ford Classification Challenge. Available online : http://www.timeseriesclassification.com/dataset.php
• An, J. and Cho, S. (2015), Variational Autoencoder based Anomaly Detection Using Reconstruction Probability, Special Lecture on IE, 2, 1-18.
• Chalapathy, R., Menon, A. K., and Chawla, S. (2018), Anomaly Detection Using One-Class Neural Networks, arXiv preprint arXiv:1802.06360.
• Chandola, V., Banerjee, A., and Kumar, V. (2009), Anomaly Detection : A survey, ACM Computing Surveys(CSUR), 41(3), 1-58. [https://doi.org/10.1145/1541880.1541882]
• Goh, B. and Baek, J. (2019), Anomaly Detection with Variational Autoencoders to Prevent System Malfunctions, Journal of the Korean Institute of Industrial Engineers, 45(2), 138-145. [https://doi.org/10.7232/JKIIE.2019.45.2.138]
• Goodfellow et al. (2014), Generative Adversarial Nets, arXiv preprint arXiv:1406.2661.
• Harmeling, S., Dornhege, G., Tax, D., Meinecke, F., and Müller, K. R. (2006), From Outliers to Prototypes : Ordering Data, Neurocomputing, 69(13-15), 1608-1618. [https://doi.org/10.1016/j.neucom.2005.05.015]
• Hochreiter, S. and Schmidhuber, J. (1997), Long Short-Term Memory, Neural Computation, 9(8), 1735-1780. [https://doi.org/10.1162/neco.1997.9.8.1735]
• Hodge, V. and Austin, J. (2004), A Survey of Outlier Detection Methodologies, Artificial Intelligence Review, 22(2), 85-126. [https://doi.org/10.1023/B:AIRE.0000045502.10941.a9]
• Kim, K., Shim, S., Lim, Y., Jeon, J., Choi, J., Kim, B., and Yoon, A. (2020), RaPP : Novelty Detection with Reconstruction along Projection Pathway, ICLR 2020 Conference.
• Kingma, D. P. and Welling, M. (2013), Auto-Encoding Variational Bayes, arXiv preprint arXiv:1312.6114.
• Lee, J., Qiu, H., Yu, G., and Lin, J. (2007), Rexnord Technical Services, Bearing Data Set, IMS, University of Cincinnati, NASA Ames Prognostics Data Repository.
• Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., and Frey, B. (2015), Adversarial Autoencoders, arXiv preprint arXiv:1511.05644.
• Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., and Shroff, G. (2016), LSTM-based Encoder-Decoder for Multi-Sensor Anomaly Detection, arXiv preprint arXiv:1607.00148.
• Olszewski, R. T. (2001), Generalized Feature Extraction for Structural Pattern Recognition in Time-Series Data, Doctoral Thesis, Carnegie-Mellon Univ., Pittsburgh,Pa School of Computer Science.
• Pidhorskyi, S., Almohsen, R., and Doretto, G. (2018), Generative Probabilistic Novelty Detection with Adversarial Autoencoders, arXiv preprint arXiv:1807.02588.
• Ruff et al. (2018). Deep One-Class Classification, In International Conference on Machine Learning, 4393-4402.
• Sabokrou, M., Khalooei, M., Fathy, M., and Adeli, E. (2018), Adversarially Learned One-Class Classifier for Novelty Detection, In Proceedings of the IEEE Conference on Compute.r Vision and Pattern Recognition, 3379-3388. [https://doi.org/10.1109/CVPR.2018.00356]