란체스터 전투모형에 기반한 방어작전에서 예비대 편성의 효과 분석
© 2021 KIIE
Abstract
This paper aims at analyzing the effect of organizing reserve force in defensive operations. Though existing studies on troop reassignment assumed that the mutual assistance of the fighting forces was possible. Relocating troops in engagement is unrealistic. Therefore, in this paper, we present a mathematical model based on Lanchester Square Attrition Model with a separate reserve force. The proposed model allows to analyze the change in the number of surviving troops according to the proportion of the reserve force, so that the effectiveness of reserve force in defensive operations can be analyzed.
Keywords:
Lanchester Square Law, Reserve Force, Defensive Operation1. 서 론
1.1 연구 배경
방어작전에서 예비대는 방어의 지속성을 보장하고 융통성을 확보하는 중요한 수단이다. 공자는 전투가 이루어지는 시간과 공간을 택하여 전투력을 집중함으로써 결정적 지점에서의 전투력 우위를 달성한다. 즉, 공자는 선택과 집중을 통해 방자를 각개격파 할 수 있다는 이점을 가지고 있다. 반면에 방자는 전투력이 분산된다는 불리함을 가질 수밖에 없다. 전장에서 지휘관이 병력을 할당하고, 전투의 흐름에 따라 재배치하는 모든 행위는 결국 주요 전투가 이루어지는 결정적 지점에서 아군의 가용 전투력을 집중시키려는 노력이라고 할 수 있으며, 방어작전에서 전투력 집중을 달성하기 위한 가장 기본적인 요소가 바로 예비대이다. 육군의 야전교범에서도 방어의 지속성을 보장하고 융통성을 확보하는 중요한 수단으로써 예비대의 중요성에 대해 언급하고 있으며, 예비대의 편성은 필수적이라고 강조하고 있다(Republic of Korea ARMY, 2017). 실제 전사에서도 예비대의 중요성에 대해 알아볼 수 있는데, 6·25전쟁 초기 남하하는 북괴군을 저지하지 못한 국군 제7사단과 방어에 성공한 국군 제6사단의 사례가 대표적이다. 의정부 지역을 방어한 국군 제7사단은 본래 1, 3, 9연대로 편성되어 있었으나 사단 예비인 제3연대가 수도경비사령부로 예속이 변경되고 충청남도 온양에 주둔하고 있던 제2사단 25연대가 배속되어 6월 15일까지 의정부로 이동하기로 계획되어 있었다. 그러나 수용시설 등의 문제로 전쟁발발 때까지 부대를 이동하지 못해 제7사단은 예비대를 보유하지 못한 채로 전쟁을 맞게 되었고, 결과적으로 북괴군을 저지하지 못해 개전 3일 만에 서울이 함락되는 결과를 맞게 되었다. 반면 중부전선의 국군 제6사단은 북괴군 2군단의 주공이 춘천을 지향하였음에도 예비대인 제19연대를 춘천에 투입하여 방어에 성공함으로써, 춘천을 돌파한 후 수원으로 우회하여 이미 서울을 점령한 북괴군 1군단과의 협공을 통해 서울에서 국군의 주력을 섬멸한다는 북괴군의 작전계획에 차질을 일으켰고, 결과적으로 국군이 전투력을 유지한 채 철수할 수 있도록 하였으며, 유엔군 참전을 위한 시간을 제공하였다(Ohn et al., 2010).
1.2 이론적 배경
Lanchester(1916)는 제1차 세계대전의 공중전 결과 분석을 통해 동일한 무기체계로 구성된 양 집단 간의 교전에서 전투력이 소모되는 양상을 미분방정식으로 표현한 전투모형을 제시하였고, 란체스터 전투모형을 통해 전투력 집중의 효과를 수리적으로 증명하였다. 현대 무기체계의 비약적인 발전에도 불구하고, 전투력 집중의 원칙은 여전히 전투의 승리를 위한 주요 원칙으로 존재하고 있으며, 란체스터 전투모형을 적용한 워게임 모델은 지금도 널리 활용되고 있다.
대표적인 란체스터 전투모형으로는 선형모형과 제곱모형이 있다. 전장에서 청군과 홍군이 전투를 벌이는 상황에서 청군의 초기 병력의 수를 B단위, 홍군의 초기 병력의 수를 R단위라고 가정하고, 각각의 단위 부대의 전투능력에 따라 결정되는 전투효율 계수를 b, r로 정의하자.
선형모형의 경우 고대 검투사의 대결과 같이 초기 병력의 수와 관계없이 오직 상대의 전투효율성에 따라 아군의 전투력 변화가 이루어지는 모형으로, 현대전에서는 포병 화력에 의한 전투를 잘 묘사하는 것으로 인정받고 있다. 선형모형을 미분방정식으로 나타내면 식 (1), (2)와 같이 나타낼 수 있다.
| (1) |
| (2) |
제곱모형은 상대방의 전투효율과 병력의 수에 따라 아군 병력의 수가 변화하는 모형으로, 제곱모형을 미분방정식으로 나타내면 식 (3), (4)와 같이 나타낼 수 있다.
| (3) |
| (4) |
제곱모형은 소총 사격을 통한 교전과 같은 현대전의 특성을 잘 반영하는 것으로 인정받고 있으며, 전투력 집중의 효과를 잘 반영하는 모형이다.
란체스터 전투모형의 기본이라고 할 수 있는 선형모형과 제곱모형 외에도 포병부대와 소총부대가 혼합된 부대의 전투를 묘사하기 위해 선형모형과 제곱모형을 혼합한 혼합모형과 아군의 규모가 클수록 아군의 피해가 크게 발생하는 로그형 모형 등이 추가로 개발되었다.
본 연구에서는 현대전의 양상을 가장 잘 반영하고, ‘예비대 편성을 통한 전투력 집중의 효과 분석’이라는 연구 목적에 적합한 제곱모형을 바탕으로 연구를 진행하였다.
1.3 기존연구 고찰
란체스터 전투모형을 통해 승리를 위한 병력의 수 또는 병력할당 방안을 다루는 연구는 과거부터 최근까지 꾸준히 이루어지고 있다. Roberts and Conolly(1992)는 2개의 공격군과 1개의 방어군 간의 교전을 다루는 (2, 1) 전투모형에서 방어군을 전멸시키기 위한 공격군의 최소 병력을 구하였고, Kaup et al.(2005)과 Sheeba et al.(2006)은 다수의 공격군과 하나의 방어군 간의 교전을 다루는 (n, 1) 전투모형에서 방어군의 최적 병력할당 문제를 다루었다. Krichman et al.(2001)은 전투를 단계화하고 단계별 적의 병력 상황에 따라 아군의 병력 할당을 변화시키며 아군의 병력 손실을 최소화하는 방안을 다루었고, Sheeba and Debasish(2008)는 서로 다른 전투효율을 가진 두 개의 공격군을 방어하기 위한 병력 할당 방안을 제시하고, 두 개의 전장 중 먼저 전투가 종료된 전장의 잔여 병력을 다른 전장에 투입함으로써 전투가 완전히 종료되었을 때 양 전장의 병력 손실의 차를 줄이고자 하였다. Wu et al.(2009)은 서로 다른 전투효율을 가진 다수의 공격군과의 전투에서 방어군의 허용 가능한 최대 전투 피해율을 고려한 병력 할당 방안을 다루었고, Hwang et al.(2018)은 (2, 2) 전투모형에서 초기에 적의 병력 할당에 대한 정보가 없을 때, 교전 발생 직후 적의 병력 할당 상황에 따라 최적의 대응을 위한 병력의 재할당 문제를 다루었다. 이 외에도 전투효율을 상수가 아닌 확률변수로 적용하여 실제 전장의 불확실성을 반영하기도 하였으며(Park et al., 2016), 세 집단 간의 전투를 묘사하여 다자간 대립 상황에서의 전투 양상을 반영하기도 하였다(Kress et al., 2018).
앞에서 기술한 바와 같이 란체스터 전투모형에 관한 연구는 과거부터 최근에 이르기까지 지속해서 이루어지고 있으며, 대부분의 연구가 아군의 병력 손실 최소화를 위한 병력 할당 문제를 다루고 있다(Roberts and Conolly, 1992, Krichman et al., 2001, Kaup et al., 2005, Sheeba et al., 2006, Sheeba and Debasish, 2008, Wu et al., 2009, Hwang et al., 2018). 하지만 방어작전의 핵심요소인 예비대를 다룬 연구는 이루어지지 않았는데, 적과 교전 중인 부대 간의 병력 지원이 자유롭게 가능한 것으로 가정하여, 예비대를 통한 병력 지원을 고려할 필요가 없었기 때문으로 추측된다. 하지만 실제 전장의 양상을 고려하면 이미 적과 교전 중인 부대의 경우 전황이 유리하다고 하더라도 병력 일부를 빼내어 전황이 불리한 전장으로 지원하는 것은 매우 어렵다. 그 이유는 적 또한 주력방향에 대한 공격작전의 성공을 위해 아군의 병력 전환을 방해하고자 고착 및 견제를 실시하기 때문이다. 따라서 실제 전장에서의 병력지원은 예비대를 통해 이루어지는 경우가 대부분이다. 그러나 육군의 야전교범에서는 적절한 예비대의 비율을 구체적으로 제시하고 있지 않으며, “예비대는 방어의 지속성을 보장하고 융통성을 확보하는 중요한 수단이다. 모든 작전이 계획대로 진행되는 경우는 드물기 때문에 우발상황이나 예기치 못한 상황에 대비한 예비대 편성과 확보는 필수적이다.”(Republic of Korea ARMY, 2017)와 같이 개념적으로만 제시되어있다. 이것이 예비대의 적정 비율에 관한 연구가 필요한 이유이다.
본 연구에서는 전선에서 교전 중인 주방어부대 간의 병력 지원은 불가능한 것으로 가정하여 실제 전장과 유사한 조건을 부여하였다. 이러한 조건에서, 예비대의 편성 비율에 따라 변화하는 전투 종료 시 생존 병력의 수를 비교하여 예비대 편성의 효과를 분석하고, 예비대가 증원되는데 소요되는 시간과 예비대 비율의 관계를 분석하여 교범상 개념적으로만 제시되어있는 적절한 예비대의 규모를 란체스터 전투모형을 통해 수리적으로 검증하고자 한다.
2. 문제 정의
2.1 문제 정의
일반적인 한국군 부대 편성은 삼각편제를 따르며, 방어작전시 전방에 2개 부대(주방어부대)를 배치하고, 예비대를 후방에 배치한다. 방어군이 2개의 방어목표 A와 B를 방어하는 상황을 가정하여 모형을 설정해보자.
연구에서 사용된 각 기호의 정의는 아래와 같다.
- ∙ x(t) : 시간 t에서의 공격군의 병력
- ∙ y(t) : 시간 t에서의 방어군의 병력
- ∙ M : 시간 t0(전투가 시작되는 시점)에서의 공격군의 전체 병력
- ∙ N : 시간 t0(전투가 시작되는 시점)에서의 방어군의 전체 병력
- ∙ β : 공격군의 전투효율
- ∙ α : 방어군의 전투효율
- ∙ yA : 전장 A에 배치된 방어군의 병력
- ∙ yB : 전장 B에 배치된 방어군의 병력
- ∙ yR : 예비대의 병력
- ∙ k : 전체 방어군 중 예비대의 비율
- ∙ tm : 예비대의 증원 소요시간
- ∙ tx wins : 전장 A(or B)에서 방어군이 전멸하는 시점의 시간(예비대 증원이 없을 때)
- ∙ ty wins : 전장 A(or B)에서 공격군이 전멸하는 시점의 시간(예비대가 증원되었을 때)
- ∙ : 예비대 증원 후(t > tm) 전장 A의 공격군의 병력
- ∙ : 예비대 증원 후(t > tm) 전장 A의 방어군의 병력
- ∙ Z : 전투 종료 후 방어군의 생존병력
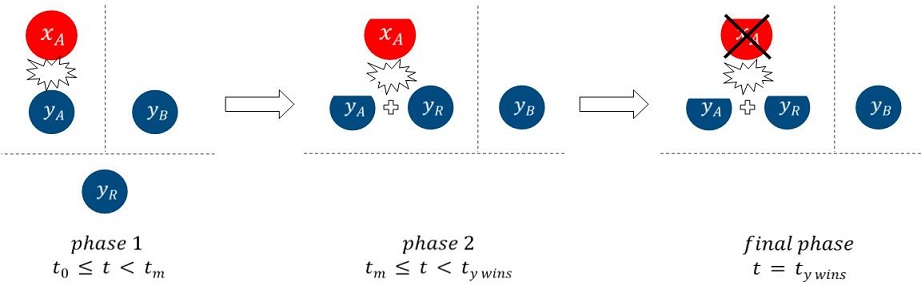
본 연구에서는 2개의 주방어부대의 병력의 수는 동일한 것(yA = yB)으로 가정하였다. 실제 전장에서는 공격군에 대한 정보를 바탕으로 주방어부대의 병력의 수에 차이를 둘 수 있지만, 이는 공격측 역시 마찬가지이므로 본 연구에서는 공격군에 대한 정보가 부족한 상황을 가정하여 주방어부대의 병력의 수는 동일한 것으로 설정하였다. 또한, 교범상 예비대는 작전지역의 시·공간상의 중앙에 위치시키는 것이 일반적이므로(Republic of Korea ARMY, 2017), 예비대는 2개의 주방어부대로부터 동일한 거리에 위치하여 공격군이 어느 방향으로 공격하더라도 증원에 소요되는 시간은 동일한 것으로 가정하였다.
위에서 정의한 기호들을 바탕으로 모형을 도식화하면 아래 그림과 같으며, 그림에서의 phase 1에 해당하는 부분은 2.4절에서, phase 2에 해당하는 부분은 2.5절에서 상세히 설명하였다.
2.2 기본적인 란체스터 제곱모형
예비대를 고려하지 않고, 하나의 공격군과 하나의 방어군을 다루는 기본적인 (1, 1) 전투모형을 다루는 제곱모형은 식 (5)와 같다.
| (5) |
아래 식 (6)은 미분방정식 (5)를 x와 y에 대한 일반식으로 표현한 식이다.
| (6) |
방어군이 승리하기 위해서는 식 (6)에서 x(t) = 0일 때, y(t) > 0을 만족하여야 한다. 따라서 방어군이 승리하기 위한 조건은 식 (7)과 같다.
| (7) |
2.3 예비대 증원 전투모형
2.2절에서는 기본적인 란체스터 제곱모형을 제시하였다. 본 절에서는 본 연구에서 설정한 전투모형에 대해 제시하였으며, 이를 ‘예비대 증원 전투모형’이라고 하였다.
앞서 2개의 주방어부대의 병력의 수가 동일한 것으로 가정하였으므로 yA = yB가 되고, 따라서 yR = N - yA - yB = N - 2yA가 된다. 전체 방어군 중 예비대로 편성한 병력의 비율을 k라고 하면, 전장 A에 배치된 방어군의 수 yA와 예비대 병력의 수 yR은 식 (8)과 같다.
| (8) |
공격군은 전장 A와 B 중 한 곳에 전투력을 집중하여 목표지역을 점령하고자 할 것이다. 본 연구에서는 전장 A와 B에 배치된 방어군 병력의 수가 동일한 것으로 가정하였으므로 공격군의 공격방향에 따른 결과의 차이는 없다. 공격군의 고착 및 견제로 인하여 전장 A와 B 상호간의 병력 지원은 불가하며, 예비대의 증원을 통한 병력 지원만 가능하다.
전장 A 또는 B 에서 전투가 시작되는 시점에 예비대가 전장으로 출발할 경우 병력이 전장까지 이동하는데 소요되는 시간을 고려해야 하고, 이를 tm으로 나타낼 수 있다. 이 경우 전장에서의 전투는 예비대가 증원되기 전(t0 ≤ t ≤ tm)과 후(tm < t)로 구분할 수 있다. 예비대 증원 전에는 최초 전장 A 또는 B 에 배치된 방어군과 공격군 사이에 전투가 이루어질 것이며, 시간 tm에 예비대가 증원되면 방어군의 수에 예비대 병력의 수인 yR을 더하여 계산할 수 있다.
2.4 예비대 증원 전 전투모형
공격군의 공격방향에 따른 결과의 차이가 없으므로, 공격군 xA가 전장 A로 공격한다고 하면, 예비대 증원 전 전장 A에서는 공격군 xA과 방어군 yA의 전투가 발생한다. 이를 2.2절에서 제시한 란체스터 제곱모형을 이용해 나타내면 식 (9)와 같다.
| (9) |
| (10) |
만약 시간 tm에 예비대가 증원되기 전에 전장 A의 방어군 yA가 전멸할 경우 전장 A가 공격군에 의해 탈취되어 기본적인 방어작전의 목적을 달성하지 못하게 된다. 즉, 공격군 xA와 방어군 yA의 전투에서 방어군 yA가 전멸하는 시점을 tx wins라고 하면, tm > tx wins일 경우 방어군은 작전 목적을 달성하지 못하며, 여기서 tx wins를 계산하면 식 (11)과 같다.
| (11) |
식 (11)을 통해 tx wins가 예비대의 비율 k에 의해 변화함을 알 수 있다. 이 때, 방어작전의 목적을 달성하기 위해서 tm ≤ tx wins을 만족해야 하므로, 예비대가 증원되는데 소요되는 시간인 tm이 결정된다면 tm ≤ tx wins의 조건을 만족하기 위한 k의 범위 역시 결정된다는 것을 알 수 있다. 예비대의 증원 소요시간은 예비대의 기동력과 작전지역의 지리적 특성 등에 의해 결정되므로 단축하는 데 한계가 존재한다. 따라서 tm ≤ tx wins의 조건을 만족하기 위해서는 예비대의 비율 k를 적절히 설정해야 함을 알 수 있다.
2.5 예비대 증원 후 전투모형
tm ≤ tx wins를 만족하여 yA가 전멸하지 않고 시간 tm에 예비대 yR이 전장 A에 증원되어 전투에 참여한다면, tm까지 전투를 통해 소모된 공격군 xA(tm)과, 방어군 yA(tm)에 증원된 예비대 yR이 더해진 방어군 yA(tm)+yR이 전투를 실시하게 될 것이다. 따라서 시점 tm에서는 새로운 소모방정식을 적용해야 하며, t ≥ tm일 때 전장 A에서의 공격군과 방어군의 수를 각각 와 라고 하면 식 (12)와 같다.
| (12) |
또한,
| (13) |
이 때, 전장 A에서 xA가 전멸하여 전투가 종료되는 시점을 ty wins라고 하고, ty wins를 식 (11)과 같이 계산하면, 식 (14)와 같다.
| (14) |
이 때 방어군이 승리하기 위해서는 식 (7)에 의해 을 만족해야 한다. 이 조건을 만족할 경우 전장 A의 생존병력의 수는 가 되고, 전장 B의 방어군을 포함한 전체 방어군의 생존 병력의 수를 목적함수 Z로 두면 식 (15)와 같다.
| (15) |
본 장에서 예비대를 고려한 전투모형을 설정하였으며, 이를 바탕으로 전투 종료 후 생존 병력을 최대화하는 목적함수를 설정하였다. 이후 제3장에서는 제2장에서 도출한 식을 바탕으로 수리 실험을 진행하여 예비대의 증원 소요시간과 설정 가능한 예비대 비율의 관계 및 전투 종료 후 생존병력의 수와 예비대의 비율과의 관계 등을 분석한다.
3. 예비대 편성의 효과 분석
예비대 편성의 효과를 검증하기 위해 크게 3가지 경우로 나누어 분석을 진행하였다. 첫 번째는 방어군이 크게 우세하여 예비대의 편성 여부와 관계없이 승리하는 경우이며, 두 번째는 공격군이 크게 우세하여 예비대의 편성 여부와 관계없이 패배하는 경우이다. 마지막 세 번째는 공격군과 방어군 모두 압도적인 전력을 보유하지 못하여 예비대의 편성 여부에 따라 전투 결과가 달라지는 경우이다. 첫 번째와 두 번째의 경우 예비대 편성 여부가 전투의 승패를 변화시키지는 못하지만 병력의 손실량을 비교하여 예비대 편성의 효과를 분석하였다.
3가지 경우 모두 양 군의 전투효율은 0.02단위로 동일하게 가정하였고, 방어군의 초기 병력의 수 N은 모두 1,000단위로 동일하게 가정하였다. 공격군의 초기 병력의 수 M은 첫 번째 경우에서는 400단위로 가정하여 방어군이 크게 우세한 상황을 조성하였으며, 두 번째 경우에서는 방어군과 동일한 1,000단위를 부여하여 공격군이 크게 우세한 상황을 조성하였다. 마지막 세 번째 경우에서는 공격군의 병력 M값으로 600단위를 부여하여 예비대 편성 여부에 따른 전투 결과의 변화를 관찰하였다.
3.1 방어군이 크게 우세한 경우
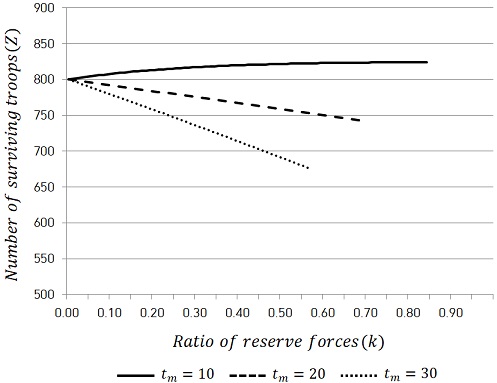
첫 번째 상황은 방어군이 크게 우세한 경우로, 방어군의 초기 병력의 수 N은 1,000단위이며, 공격군의 초기 병력의 수 M은 400단위이다. (양 군의 전투효율은 0.02단위로 동일)
<Figure 2>는 식 (15)를 이용하여 예비대의 비율 k의 변화에 따른 전투 종료 후 생존병력의 수 Z의 변화를 나타낸 그래프이다. 실선은 tm(예비대의 증원 소요시간)이 10단위시간일 때를 나타내며, 긴 점선과 짧은 점선은 각각 tm이 20과 30단위시간일 때를 나타낸다. <Figure 2>에서 tm이 10일 때는 k(예비대의 비율)이 커짐에 따라 미세하지만 Z 역시 커지는 것을 알 수 있으나, tm이 20 또는 30일 때는 오히려 감소하는 것을 확인할 수 있다. 이를 통해 방어작전시 방어군이 공격군에 대하여 크게 우세할 경우 예비대의 증원 소요시간에 따라 예비대를 편성하는 것이 오히려 비효율적인 경우도 존재한다는 사실을 알 수 있다.
3.2 공격군이 크게 우세한 경우
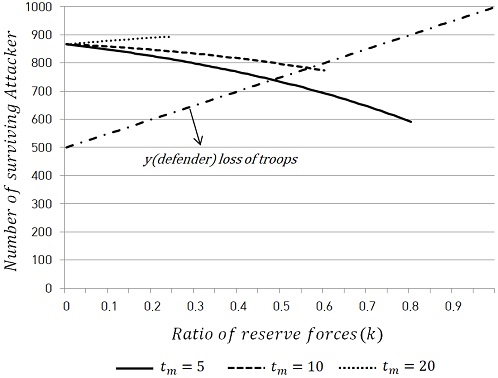
두 번째 상황은 공격군이 크게 우세한 경우로, 방어군의 초기 병력 수 N은 1,000단위로 동일하며, 공격군의 초기 병력 수 M은 1,000단위이다. (양 군의 전투효율은 0.02단위로 동일)
이 경우 예비대 편성 여부와 관계없이 방어군은 방어에 실패하게 되므로, 첫 번째 상황과 같은 그래프를 활용하는 것은 적절하지 않다. 따라서 이 경우에는 방어군이 아닌 공격군의 생존병력의 수와 예비대의 비율 간의 관계를 분석하였다.
<Figure 3>은 식 (6)과 (12)를 이용하여 예비대의 비율 k의 변화에 따른 공격군(x)의 생존병력의 변화를 나타낸 그래프이다. 실선은 tm(예비대의 증원 소요시간)이 5단위시간일 때를 나타내며, 긴 점선과 짧은 점선은 각각 tm이 10과 20단위시간일 때를 나타낸다. <Figure 3>을 통해 tm이 5 또는 10인 경우 예비대의 비율 k가 증가함에 따라 공격군의 생존병력의 수는 감소하지만, tm이 20인 경우 오히려 증가하는 것을 알 수 있다. 이를 통해, 예비대의 증원 소요시간이 긴 경우 예비대를 편성하는 것이 병력이 각개격파되는 결과를 불러일으킬 수 있다는 것을 알 수 있다. 또 한 가지 알 수 있는 사실은, 공격군이 크게 우세한 경우 예비대의 증원 소요시간이 짧더라도 예비대를 투입하는 것이 효율적이지 않다는 것이다. 그래프의 파선-점선은 예비대의 비율 k에 따른 방어군(y)의 병력 손실을 의미하며, 이는 증원 소요시간 tm과는 무관하다. 그래프의 기울기를 통해 tm이 5 또는 10일 때에도 예비대의 비율 변화에 따른 공격군의 병력 손실보다 방어군의 병력 손실이 더 크다는 것을 알 수 있다.
3.3 공격군과 방어군이 대등한 경우
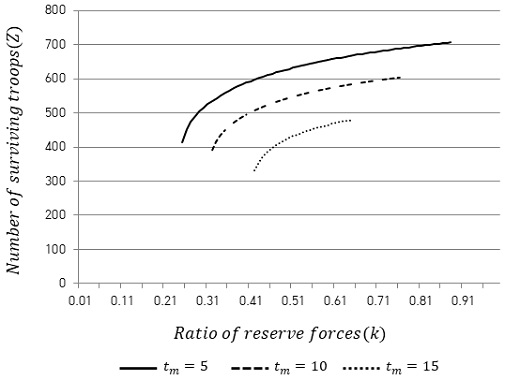
세 번째 상황은 예비대의 편성 여부에 따라 결과가 달라지는 경우로, 방어군의 초기 병력의 수 N은 1,000단위로 동일하며, 공격군의 초기 병력의 수 M은 600단위이다. (양 군의 전투효율은 0.02단위로 동일)
<Figure 4>는 식 (15)를 이용하여 예비대의 증원 소요시간 tm이 각각 5시간(실선), 10시간(긴 점선), 15시간(짧은 점선)일 때, 예비대의 비율 k에 따른 전투 종료 후 생존 병력의 수 Z의 변화를 계산한 결과다. k가 그래프에 도식된 범위 밖에 있는 경우 방어군이 패배하여 생존 병력의 수 계산이 의미가 없으므로, 방어군이 승리하였을 때의 Z를 계산하였다.
<Figure 4>를 통해 두 가지 중요한 사실을 알 수 있다. 첫 번째는 예비대 편성에 적정 비율이 존재한다는 것이다. 예비대의 비율이 너무 작은 경우 전투력 집중의 효과를 충분히 달성하지 못하여 전투에서 패배하였으며, 비율이 너무 큰 경우 예비대 증원 이전에 주방어부대가 전멸하여 전투에서 패배하였다. 따라서 승리를 위해서는 적절한 예비대의 비율을 설정해야 한다.
두 번째는 예비대의 비율이 과도하게 높아 예비대 도달 이전에 주방어부대가 전멸하는 상황이 되지 않는다면, 예비대의 비율이 높을수록 아군의 생존병력의 수가 커진다는 것이다. 이는 예비대를 통해 전투력 집중의 효과를 얻을 수 있으며, 이를 통해 전투를 보다 효율적으로 수행할 수 있음을 의미한다.
4. 결 론
본 논문에서는 그동안의 란체스터 전투모형에 관한 연구에서 다루지 않은 예비대 편성의 효과에 대해 분석하였다. 실제 전장에서 이미 전선에서 적과 교전 중인 병력을 재배치하는 것은 매우 어려운 일이기에 방어작전에서 지휘관의 지휘역량은 예비대를 얼마나 적시적소에 운용하는가에 달려있고, 그에 앞서 적절한 규모의 예비대를 편성하는 것도 아주 중요하다. 따라서 란체스터 제곱 모형을 응용한 예비대 증원 전투모형을 제시하였으며, 예비대의 증원 소요시간과 적절한 예비대 비율의 관계를 분석하였다.
분석은 3가지 경우로 나누어 진행하였으며, 첫 번째 상황인 방어군이 크게 우세한 경우 예비대를 편성하는 것이 반드시 좋은 결과를 내는 것은 아니었다. 이 경우 예비대의 증원 소요시간이 짧은 경우 예비대를 보유하는 것이 효율적일 수도 있겠으나, 증원 소요시간이 긴 경우 오히려 예비대를 보유함으로써 우세한 병력의 이점을 잃어버리는 결과가 발생하기도 하였다.
두 번째 상황인 공격군이 크게 우세한 경우에는 예비대의 편성 및 투입이 적의 병력손실을 증가시키기도 하였으나, 적의 병력손실 증가량 대비 아군의 병력손실 증가량이 더 크므로 효율적이지 못하였다.
마지막으로 양측이 대등한 병력을 보유한 상황에서는 예비대를 보유하는 것이 효과가 있었다. 이 때, 적절한 예비대의 비율을 설정하는 것이 중요하며, 예비대의 비율이 너무 작은 경우 전투력 집중의 효과를 충분히 얻지 못하였으며, 예비대의 비율이 너무 큰 경우 예비대 증원 이전에 주방어부대가 전멸하여 방어에 실패하는 경우가 발생하였다.
결론적으로, 공격군과 방어군 중 어느 한쪽이 크게 우세할 경우에는 예비대를 편성하는 것이 무조건 효과적이라고 할 수 없었다. 하지만, 양측이 대등한 전력을 보유하고 있을 경우에는 적절한 규모의 예비대를 편성하는 것이 전투를 승패를 가르는 중요한 요소임을 확인하였다.
본 연구는 이전의 선행연구에서 다루지 않은 ‘예비대’라는 개념을 적용하였고, 예비대 편성의 효과와 적절한 비율의 예비대 편성의 필요성을 수리적으로 검증하였다는 점에 의의가 있다. 하지만, 적에 대한 정보가 충분하지 않은 상황을 가정하여 두 개의 주방어부대의 전투력이 동일한 것으로 전투모형을 설정하였기 때문에 일반화하여 적용하기 어렵다는 한계가 존재한다. 차후 연구에서 이러한 한계를 보완하기 위해 두 개의 주방어부대의 전투력을 각각의 변수로 두는 전투모형을 설정한다면, 이러한 한계를 극복할 수 있을 것이다. 또한, 후속연구에서 본 연구에서 분석한 예비대 편성의 효과를 실제 전사를 통해 검증한다면 주장에 대한 신뢰성을 높일 수 있을 것이다.
References
-
Hwang, J. H., Choi, Y. H., Park, S. H. and Lee, Y. H. (2018), Optimal Support of Military Force Based on (2, 2) Lanchester Square Attrition Model, Journal of the Korean Institute of Industrial Engineers, 44(3), 198-205.
[https://doi.org/10.7232/JKIIE.2018.44.3.198]

-
Kaup, G. T., Kaup, D. J. and Finkelstein, N. M. (2005), The Lanchester (n, 1) Problem, Journal of the Operational Research Society, 56(12), 1399-1407.
[https://doi.org/10.1057/palgrave.jors.2601936]

-
Kress, M., Caulkins, J. P., Feichtinger, G., Grass, D. and Seidl, A. (2018), Lanchester Model for three-way Combat, European Journal of Operational Research, 264(1), 46-54.
[https://doi.org/10.1016/j.ejor.2017.07.026]

-
Krichman, M., Ghose, D., Speyer, J. L. and Shamma, J. S. (2001), Theater Level Campaign Resource Allocation, In American Control Conference, Proceeding of the 2001, IEEE, 6, 4716-4721.
[https://doi.org/10.1109/ACC.2001.945727]

- Ohn, C-I., Kim, G-S., Park, I-S., Na, J-N., and H, J-N. (2010), 60th Battle of the Korean War, Hwang-geum al, Seoul, Korea.
-
Park, D., Kim, D., Moon, H. and Shin, H. (2016), Gaussian Approximation of Stochastic Lanchester Model for Heterogeneous Forces, Journal of Korean Institute of Industrial Engineers, 42(2), 86-95.
[https://doi.org/10.7232/JKIIE.2016.42.2.086]

- Republic of Korea ARMY (2017), FM Standard-3-1 Tactics.
-
Roberts, D. M. and Conolly, B. W. (1992), An Extension of the Lanchester Square Law to Inhomogeneous Forces with an Application to Force Allocation Methodology, Journal of the Operational Research Society, 43(8), 741-752.
[https://doi.org/10.1057/jors.1992.112]

-
Sheeba, P. S. and Ghose, D. (2006), Optimal Resource Partitioning in Conflicts based on Lanchester (n, 1) attrition model, 2006 American Control Conference, IEEE.
[https://doi.org/10.1109/ACC.2006.1655428]

-
Sheeba, P. S. and Ghose, D. (2008), Optimal Resource Allocation and Redistribution Strategy in Military Conflicts with Lanchester Square Law Attrition, Naval Research Logistics (NRL), 55(6), 581-591.
[https://doi.org/10.1002/nav.20303]

-
Wu, S. and Yang, J. (2009), Optimal Military Strength Allocation for Campaign between Single-kind Arms and Multi-kind Arms, 2009 International Conference on Management Science and Engineering, IEEE.
[https://doi.org/10.1109/ICMSE.2009.5317471]

오정택 : 육군사관학교 응용물리학과에서2014년 학사학위를 취득하고 국방대학교에서 국방과학학과 석사과정에 재학 중이다.연구 분야는 최적화, 무기체계 획득관리다.
마정목 : 육군사관학교 운영분석학과에서2002년 학사, 미국 펜실베니아 주립대(PSU)에서2008년 산업공학 석사, 미국 일리노이대(UIUC)에서 2015년 산업공학 박사학위를 취득하였다. 2015년부터 국방대학교 국방과학학과 교수로 재직하고 있다. 연구 분야는 국방 모델링 및 데이터 분석학, 무기체계 획득관리다.